《计算机视觉》中的几何变换：Python示例的直观解释

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

图片由Payton Tuttle在Unsplash提供

几何变换是任何图像批量处理中最常见的变换操作之一。在今天的文章中，我们将讨论其中的三种变换：旋转、平移和缩放，然后仅仅使用Numpy库，从零开始构建它们。图1显示了我们想要在视觉上达到的效果。好，下面我们开始！

图1，我们的目标是按时钟方向旋转图像a 45度，生成图像b，引用的图片来自具有CC许可证的COCO数据集。

OpenCV方式

如果您使用任何像OpenCV或PIL内置函数这样的图像库，实现上述功能非常简单。使用OpenCV，我们可以用两行代码来完成这项工作，如下所示。

import cv2
img = cv2.imread("./datasets/coco2017/val2017/000000001296.jpg")img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
center = (img.shape[1]//2, img.shape[0] //2) # Get the image centerrotation_matrix = cv2.getRotationMatrix2D(center, -45, 1) # Calculate the rotation matrixnew_img = cv2.warpAffine(img, rotation_matrix, (img.shape[1], img.shape[0])) # Transform input image

使用OpenCV旋转图像

图2，使用固定边界旋转

我们得到了图2的图像作为结果。请注意，OpenCV不会自动扩展图像的边界。为了确保我们看到整个旋转图像，我们需要做两件额外的事情。首先，计算目标图像的大小；其次，由于新图像的中心与原始中心不同，我们需要考虑旋转矩阵中中心值的差异。有了这些补充，我们就是最棒的！

original_four_corners = [(0, 0, 1), (427, 0, 1), (0, 640, 1), (427, 640, 1)]new_corners = [np.matmul(rotation_matrix, pt) for pt in original_four_corners]
min_x = np.min([pt[0] for pt in new_corners])max_x = np.max([pt[0] for pt in new_corners])min_y = np.min([pt[1] for pt in new_corners])max_y = np.max([pt[1] for pt in new_corners])new_dimensions = (int(max_y-min_y), int(max_x-min_x))print("Dimesnions of our new image should be: ", new_dimensions)
new_center = (new_dimensions[0] //2, new_dimensions[1] //2)center_translation = (new_center[0] - center[0], new_center[1] - center[1])rotation_matrix[0][2] += center_translation[0]rotation_matrix[1][2] += center_translation[1]new_img2 = cv2.warpAffine(img, rotation_matrix, new_dimensions)

动态边框旋转

这次的旋转包括了我们预期的整个图像！让我们来分析一下这些调用函数背后到底发生了什么。

旋转矩阵

我们使用上面的getRotationMatrix2D（）方法（代码段1第5行）创建了一个旋转矩阵，我们随后使用它来对原始图像变形（代码段1第6行）。该函数以图像中心、旋转角度和比例因子为参数，并返回一个旋转矩阵。这个旋转矩阵到底是什么？问题需追溯到线性代数中。让我们考虑一个任意的二维点[x，y]，那么旋转操作可以用下面的矩阵运算来表示。

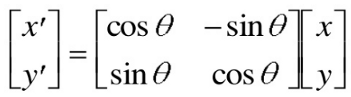
二维旋转变换

其中，R是旋转矩阵

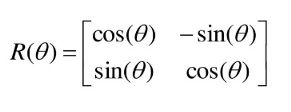
旋转矩阵R

更简单地说，旋转矩阵给了我们“函数f”x'，y'=f（x，y），它将一个输入点映射到它的旋转对应点。矩阵R由两列向量组成，这两列向量表示变换后初始基向量的最终位置（如果你像我一样是3blue1brown的粉丝，这将引起你的注意！）。

点旋转示例

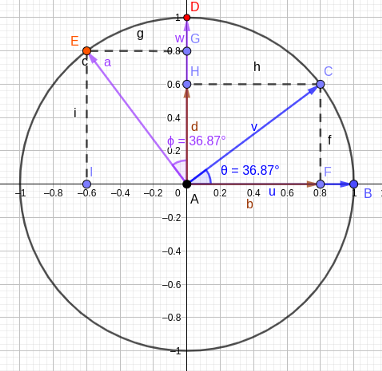
让我们用一个圆作为示意图把事情弄清楚。

在这个示意图中，考虑两个矢量u，顶点在B=[1，0]和w，顶点在D[0，1]处。然后，这些向量围绕圆心A（原点=[0，0]）旋转一定角度θ，（=phi），之后它们分别落在点C和E。

经过变换后，向量v可以用其顶点分别为F和H的正交投影向量来表示。利用基本三角法，记住向量v和a都有单位长度，我们可以很容易地看出，顶点在F的向量的长度是b=cos（θ），顶点在H的向量的长度是d=sin（θ）。

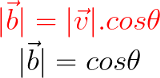
求向量v的正交分量

因此，向量v可以表示为列向量[cos（θ）sin（θ）]。类似地，我们可以证明向量a可以表示为列向量[-sin（θ）cos（θ）]。负号表示方向。

把这些列向量放在一起就得到了旋转矩阵R。为了便于矩阵相乘，通常在旋转矩阵上加一个第三方轴。直观地说，这将是旋转轴，通过它可以旋转三维结构。此轴上的所有点在变换后将保持不变，因此，此附加轴对其变换没有丝毫影响。

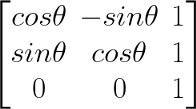
旋转变换

类似地，平移操作可以用如下所示的平移矩阵表示，其中tx和ty是X和Y方向上的平移量

。

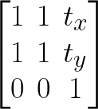平移变换

我们的缩放矩阵，其中Sx和Sy是x和y方向的缩放因子

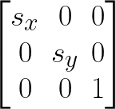
缩放变换

注：一般情况下，旋转和平移组合成一个变换矩阵，如下所示。它的作用与通过绕原点旋转θ度，然后通过tx和ty进行平移的效果相同

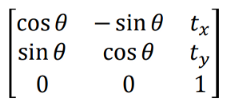
旋转和平移操作压缩到一个矩阵中

试试看！用上面的任何一个矩阵，给它们一些值，然后任意的乘以一个点[x，y]，看看变换后的点值是否是您所期望的！

我们现在有了表达几何变换所需的所有知识点。只有几件重要的事情要记住：

1、矩阵乘法是不可交换的，即如果你把两个矩阵A和B相乘，A.B！=B.A.因此，我们变换的顺序很重要。旋转一个点然后进行平移与先平移该点然后做相同的旋转是不一样的！

2、矩阵乘法的表达式变换是从右到左的。

3、由于坐标方向的重要性，需要注意你的坐标轴。和OpenCV一样，大多数图像结构都是把左上角的原点作为坐标原点。这不是我们写方程的传统“第一象限”，而是“第四象限”。实际y轴的方向是相反的。我们可以直接将其放入旋转矩阵中，或者在计算过程中添加负号（我做了第二个操作，以使变换操作与本文保持一致）。

4、旋转通常是围绕图像的中心进行。

很好，现在让我们回到原始图像，看看为了获得所需的变换图像，我们需要做些什么。具体操作顺序如下：

1、平移图像，使用图像的中心作为原点。这是因为我们希望旋转图像的中心，而不是左上角，它通常是图像中的原点像素/坐标。设这些平移因子为[tx1，tx2]。

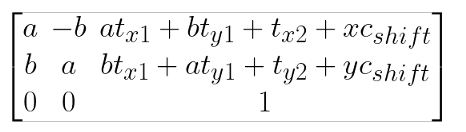
2、将图像旋转到所需的角度θ；

3、将图像平移回其原始坐标原点。我们将其归纳为[tx2，ty2]；

4、计算新坐标原点，用这些新坐标原点和旧坐标原点之间的差异平移图像。也要考虑新的图像大小（我们已经为OpenCV计算做了这一步）。将这些变换因子设为[cx_shift，cy_shift]

用矩阵的形式，我们可以将上述四个步骤表示如下。从右到左，我们将中心平移到原点（从右开始的第一个矩阵），绕中心旋转并向后平移中心（中心矩阵），最后调整中心以适应新的尺寸（第一个矩阵形式为左）。

我们的旋转矩阵

我们在这里没有使用缩放变换，但是如果你想缩放你的图像，只需要将缩放变换添加到上面的等式中（在正确的地方！）。简化上述内容并替换a=cos（θ），b=sin（θ）

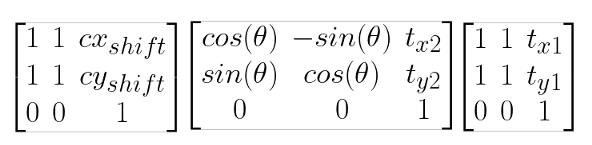简化版旋转矩阵

这是我们最后的旋转矩阵，我们将在下一节中使用Numpy来旋转图像。

Numpy方式

调用OpenCV方法既快又简单，但没有乐趣！所以我们将把我们讨论过的所有东西都整合成代码，然后仅仅使用Numpy旋转图像！

由于此脚本有点太长，无法粘贴到此处，请查看下面的链接以获取完整代码。

https://github.com/borarak/imutils/blob/master/geometric/rotate.py

从此，我们可以使用我们自己的函数旋转和平移图像！

from geometric.rotate import get_rotation_matrix, rotate_imagefrom PIL import Imageimport numpy as np
img = np.asarray(Image.open("./datasets/coco2017/val2017/000000001296.jpg").convert('L'))
rot_matrix = get_rotation_matrix(img, angle=45, adjust_boundaries=True)
rotated_image = rotate_image(img, rot_matrix)

今天到此为止，希望你喜欢。一如既往，感谢您的阅读！

 End 

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~