拉格朗日乘子法的来历与直观解释-技术圈

在开始挖历史考古之前，我们先来看一个简单的例子热热身。假设要我们求解函数在约束下的极值。

在使用拉格朗日乘子（或乘数）法时，引入约束函数，

g(x, y)=x^{2}+y^{2}-1=0.

构造拉格朗日函数，

\begin{aligned} \mathcal{L}(x, y, \lambda) &=f(x, y)+\lambda \cdot g(x, y) \\[0.5em] &=x+y+\lambda\left(x^{2}+y^{2}-1\right). \end{aligned}

然后，计算拉格朗日函数的梯度，

\begin{aligned} \nabla_{x, y, \lambda} \mathcal{L}(x, y, \lambda) &= \left[\frac{\partial \mathcal{L}}{\partial x}, \frac{\partial \mathcal{L}}{\partial y}, \frac{\partial \mathcal{L}}{\partial \lambda}\right]^{\top}\\[1.0em] &= \begin{bmatrix} 1+2 \lambda x\\ 1+2 \lambda y\\ x^{2}+y^{2}-1 \end{bmatrix} \end{aligned}

根据极值点梯度为，得

\begin{array}{c} \nabla_{x, y, \lambda} \mathcal{L}(x, y, \lambda)=0 \\ \qquad \\ \Updownarrow \\ \qquad \\ \left\{\begin{array}{l} 1+2 \lambda x=0 \\ 1+2 \lambda y=0 \\ x^{2}+y^{2}-1=0 \end{array}\right. \end{array}

注意，最后一个方程就是约束。

由前两个方程得，

x=y=-\frac{1}{2 \lambda}, \quad \lambda \neq 0

代入最后一个等式，得，

\lambda=\pm \frac{\sqrt{2}}{2}

从而得到的两个驻点，

\left[\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right], \quad\left[-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right]

代入目标函数得，

f\left[\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right]=\sqrt{2}, \quad f\left[-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right]=-\sqrt{2}

因此，在该约束下函数的最大值为，最小值为。对照下图，可以看到最大值出现在处，而最小值出现在处。

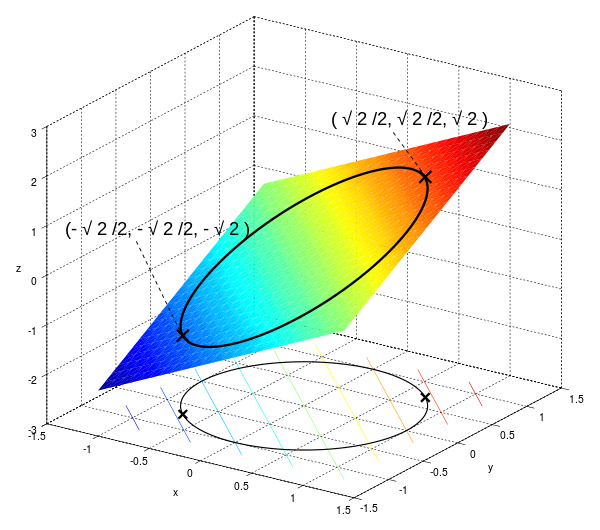
拉格朗日乘子法

本文只看针对单个等式约束的优化问题的拉格朗日乘子法，由目标函数和一个乘子乘以约束函数来构造如下拉格朗日函数，

\mathcal{L}(x, y, \lambda)=f(x, y)+\lambda \cdot g(x, y)

其中，前面可正可负。如果是原始约束问题的极值，则存在，使得是拉格朗日函数的驻点。

疑问

看上面的乘子法的使用过程，一气呵成，非常流畅吧。那么问题来了，为什么通过一个乘子将目标函数和约束函数一连组成新的目标函数就能搞定原问题呢。

1直观解释

在回顾拉格朗日乘子法的来历之前，先从几何或力学上来直观地解释一下它的原理。

单个函数的情况

首先，不妨来打个比喻，把函数看成一个正能量场，当质点或人处于这个正能量场中时，会受到周围值高处的吸引。假设人是好同志，受到正能量的驱使会往函数值大的地方移动，所谓人往高处走嘛。不过怎么吸引呢？周围各个方向上都要考虑啊。

这么说或许不够清晰，改一下，函数值在这里其实并不重要，重要的是跟周围值的差异。如果你所处点的值不是局部最大，自然会收到周围的吸引。那么，我们把这种差异和吸引用一个向量来表示非常合适，因为向量既有方向又有大小。这样的话，受到多大的吸引，往哪里走都明确了。那这个向量怎么确定呢？

有个很好的候选者，就是大家都知道的梯度向量。梯度表示函数在该点处的方向导数（有无穷多个）沿着该方向取得最大值，即函数在该点处沿着梯度方向变化最快，所谓差异最大。

如下图所示的一个 2D 函数极其梯度场。上方蓝色框线图是函数值，下方红色箭头表示函数的梯度场，我们可以把每个点上的梯度向量想象成力（有大小、有方向）。

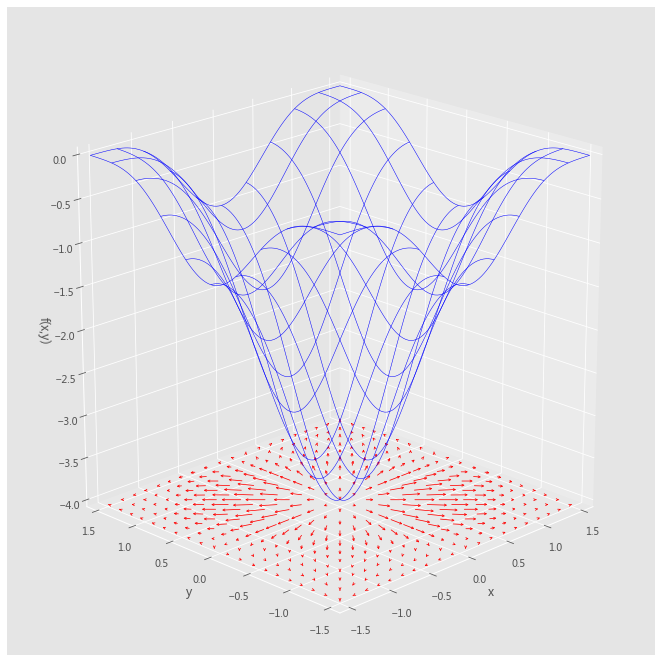
上图是

f(x,y) = -(\cos^2x + \cos^2y)^2

对应的函数值以及梯度示意图。

这里我们不妨假设: 把某点的梯度向量看成该点受到的周围外力的合力。也就是在每点处，这个梯度不为 0 的话，放在该点处的质点就会运动。

再设想一下，让无数质点充满 2D 定义域平面，然后判断它们在力场的作用下是否能够保持不动？那些保持不动的点就是我们要找的极值点。

但注意，我们这里不是像梯度下降法那样让质点在梯度场的驱动下作运动，然后迭代式找到最优值，而是让质点静态地充满整个世界（定义域），然后判断每个质点是否处于一个平衡态。只在乎那些处于平衡态的质点，即在周围力场的合力作用下保持静止的那些质点，而忽略那些有移动趋势的不安定分子。

加上约束函数

上面是单个函数的情况，但是假设你所处在两个函数的梯度场中会如何呢？那么每一点都有两个力，分别对应两个函数在该点处的梯度。

但是，此时第二个函数是起到约束的作用，而现在的问题是要找到第一个函数在约束区域中的极值。

那么这种情况下，是否也有处于平衡态的质点呢？现在问题变了，这个所谓平衡态应该也有所不同了。

这个时候，在约束区域内不一定存在目标函数（第一个函数）梯度向量（合力）为 0 的情况。那质点如何处于静止状态呢？

将约束函数的梯度向量看成虚力，通过放大或缩小后与目标函数的梯度向量（力）达成一种平衡。

合力为 0，或者
合力不为 0，但力的方向与质点能移动的方向正交。

这两者合为一种，就是目标函数的梯度向量与约束函数的梯度向量平行！看下图，蓝色代表目标函数，绿色代表约束函数。如果方向不平行，质点就会沿着垂直于绿色箭头的方向（即绿线的切线方向），使得质点沿着这个方向（即往函数值更高/低处）移动。

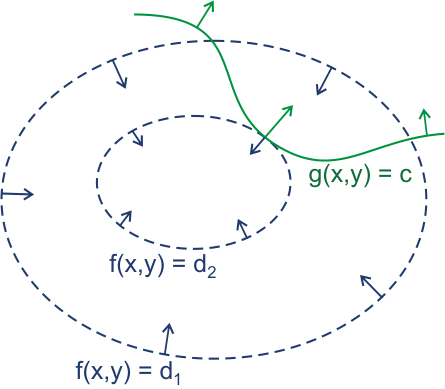
这里重要的是力的方向，而力的大小可以通过引入一个缩放因子来平衡，这个因子就是所谓的乘子。

好了，直观解释已经讲完了，那么这个方法是因为什么背景问题提出来的呢？让我们来看看拉格朗日当初提出乘子法求解带约束的最优化问题时的背景。

2乘子法的动机

拉格朗日在 1764 年的回忆录中提出了他的这一新概念，该回忆录旨在回答巴黎学院 1762 年提出的有关月球天平动问题。1780 年，他概述了该方法的更为详尽的通用版本，并最终在 1788 年发表了这个方法。在 1811 年出版的第二版中，拉格朗日强调了乘子对约束优化的重要性。

约瑟夫·拉格朗日（Joseph-Louis Lagrange，1736~1813）

拉格朗日的想法有两个明确的来源，

第一个是伯努利（Bernoulli）虚速度原理，适用于由中心力驱动的质点系统平衡问题。
第二个来源是达朗贝尔（d'Alembert）的动力学原理。

拉格朗日是在所谓静力学的框架内引入了这种数学方法，以便确定约束问题的一般平衡态方程。

拉格朗日在《Mécanique Analytique》一书中论述了静力学，并提出了三项原理作为该主题的基础，

杠杆原理；
力的合成原理；
虚速度原理。

所谓虚速度，指的是处于平衡态的物体在平衡被中断时所获得的速度；是为了建立方程而假设的速度，不是真实速度。

如果我们仅考虑两个力和施加到质点上，并且如果和是物体受到的分别来自和的虚速度，那么如果满足如下等式，则说明质点达到平衡态。

P \frac{d p}{d t}+Q \frac{d q}{d t}=0

这个公式表示如果所有力的虚功率之和为 0，那么质点将处于平衡状态。量表示力对应的功率（单位时间内力做的功）。

在从数学角度处理该物理问题时，拉格朗日用乘以两边，即用代替。

因此，例如质点受到三个力时的平衡态对应的一般方程为，

Pdp+Qdq+Rdr=0

这样，拉格朗日能够以更一般、更简单的方式解决问题。特别是，他详细研究了约束条件下的平衡。他首先检查了带约束的质点的平衡态，如考虑两个约束。从物理角度来看，和被视为力，而和表示由这些力做的虚功。

此时，这个微分方程的一般形式是

P d p+Q d q+\cdots+\lambda d L+\mu d M \cdots=0.

这样的方程是描述平衡态的一般方程。

如果考虑正交参考系，那么每个变量将对应一个平衡态方程。例如，在方向上，有

P \frac{d p}{d x}+Q \frac{d q}{d x}+\cdots+\lambda \frac{d L}{d x}+\mu \frac{d M}{d x} \cdots=0.

该方法的优点是，它允许以与无约束问题相同的方式来处理带约束的优化问题。这种方法的第一个极其重要的结果是，对于约束的分析和数值处理被转化到平衡条件上。

拉格朗日从数学的角度指出，困难在于确定、等的值。实际上，这点不难搞定，因为加上约束本身，方程数和变量数是相同的。

举个例子，如果有两个力和以及由等式表示的约束。假设在三维空间中，将具有三个未知量和未知乘子，我们将得到四个方程，

\begin{aligned} P \frac{d p}{d x}+Q \frac{d q}{d x}+\lambda \frac{d L}{d x} &=0 \\ P \frac{d p}{d y}+Q \frac{d q}{d y}+\lambda \frac{d L}{d y} &=0 \\ P \frac{d p}{d z}+Q \frac{d q}{d z}+\lambda \frac{d L}{d z} &=0 \\ L &=0 \end{aligned}

这样，从数学的观点来看，质点的平衡问题的解似乎类似于在约束条件下求解函数的极值问题。

好了，回到上面，将函数梯度看成力是不是正是从物理的角度来解释这个数学最优值问题呢。

把上面前面几个式子中的第三项移位一下，

\begin{aligned} P \frac{d p}{d x}+Q \frac{d q}{d x} &= \hat{\lambda} \frac{d L}{d x} \\ P \frac{d p}{d y}+Q \frac{d q}{d y} &= \hat{\lambda} \frac{d L}{d y} \\ P \frac{d p}{d z}+Q \frac{d q}{d z} &= \hat{\lambda} \frac{d L}{d z} \\ L &=0 \end{aligned}

前几个方程理解为质点处于平衡状态的条件，最后一个式子（约束函数本身）看成对位子的约束，即相当于将带约束的优化问题转化为限制在一定区域内寻找处于平衡状态的质点。

3实例解读

这里借用国外某个网站讲解 SVM 的例子中的图片来可视化本文一开始的例子，但仔细看目标函数和约束函数刚好对调了。

考虑如下优化问题，

\begin{array}{ll} \underset{x, y}{\operatorname{minimize}} & f(x, y)=x^{2}+y^{2} \\ \text { subject to } & g(x, y)=x+y-1=0 \end{array}

目标函数和约束函数的等值线图如下所示，

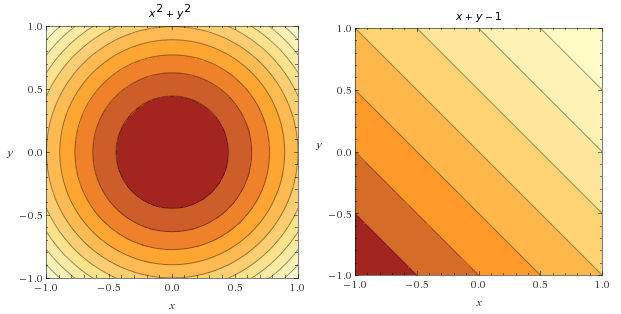
值得注意的是，可以在一个图上同时展示这两个等值线图来可视化这两个函数。下图中，可以看到由蓝色线条描述的约束函数。这里画了目标函数的几个梯度向量（黑色箭头）以及约束函数的两个梯度向量（白色箭头）加以对比。

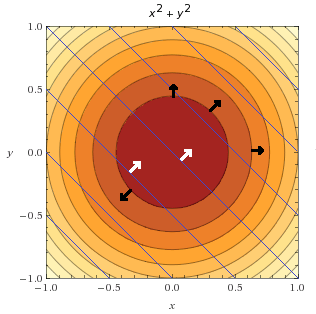
假定考虑的范围为。下图中，在目标函数上叠加画出了的蓝色直线，这条线也被称为可行集。

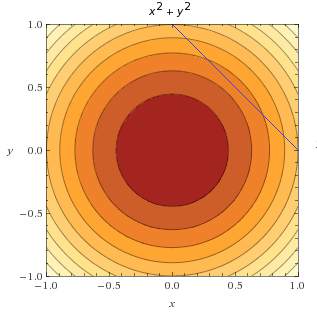
按照拉格朗日乘子法的动机分析，当两个函数的梯度向量平行时，将获得在约束下的目标函数的最小值。

在下图中，可以看到目标函数的等值线与可行集相切的点。另外，为了对比，还添加了目标函数在可行集上其他地方的梯度向量（黑色箭头）以及对应的约束梯度向量（白色箭头）。

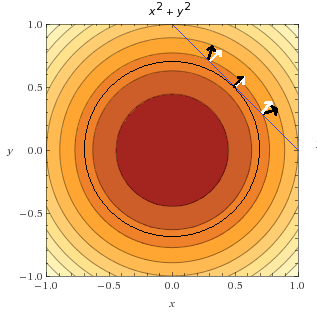
可以看到，这个问题中，在可行集上只有在一个点处两个函数的梯度向量平行（指向相同方向），该点处的函数值正是在该约束下目标函数的最小值。

小结与下期预告

本文针对求解带单个等式约束条件的函数最优化问题的拉格朗日乘子法，探讨了它诞生的背景、大概动机以及直观解释。也许有些地方有待改进，欢迎提出纰漏或者更好的想法。

下期将送上关于矩阵与拉格朗日乘子法的一段经典联袂演出。

拉格朗日乘子法的来历与直观解释