首先，看一眼多元向量值函数 的雅可比矩阵，

什么叫多元向量值函数呢？就是输入一个向量（ 维），函数输出一个向量（ 维）。也可以看成 个 元数量函数，所以上面矩阵中数量函数 的下标最大到 。

1简要回顾

雅可比在 1841 年的论文中针对 个 元函数的相关性，提出了所谓的雅可比行列式，如果这个行列式不为 ，则这些函数是独立的。因此，他提出的也叫函数行列式。虽然他没有单独提出上面那个矩阵，但是等到后来有了矩阵的概念，人们还是将其称为雅可比矩阵。

雅可比行列式是坐标变换理论的基础之一，在数学分析隐函数理论中发挥着重要作用。

另外，函数偏导数的记法 虽然他不是第一个使用，在他之前有人零星使用过，但是在他那篇论文之后才正式得到广泛使用。

2雅可比矩阵的用途

仿射变换

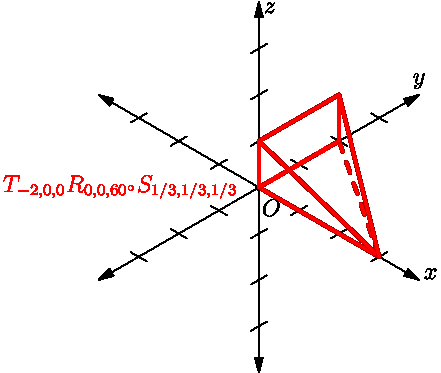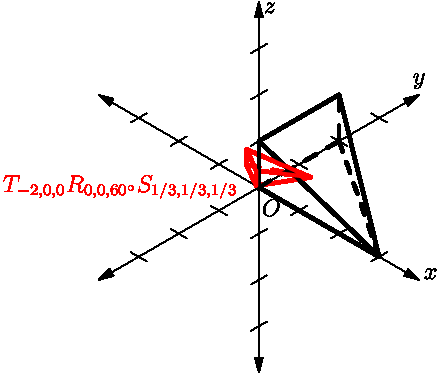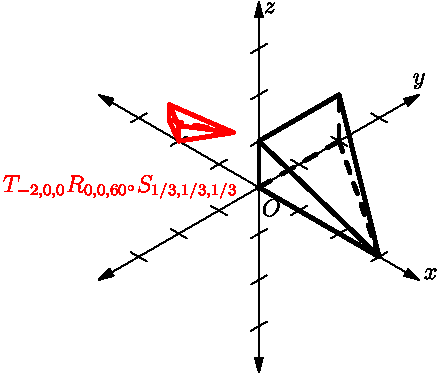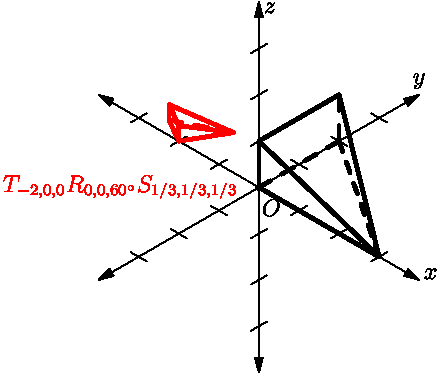
所谓仿射变换（或者叫仿射映射），就是两个变换的复合: 线性及平移。具体来说，仿射变换就是指将一个向量空间进行一次线性变换再加上一次平移，变换到另一个向量空间。

定义 空间上的仿射变换为，

其中，设 是一个 的实矩阵， 是 维向量。上式中绿色框框里就是线性变换那部分，蓝色那项就是平移量。从定义上可以看出来，仿射变换是包括线性变换的。换句话说，如果平移项 ，那么这个仿射变换就是一个线性变换了。

仿射变换有两个特殊的性质：

• 1 共线不变性: 在同一条直线上的点在变换后仍然共线。
• 2 比例不变性: 直线上各点间的距离比例在变换前后保持不变。例如对共线的相异三点 ， 和 ，有，

仿射变换举例

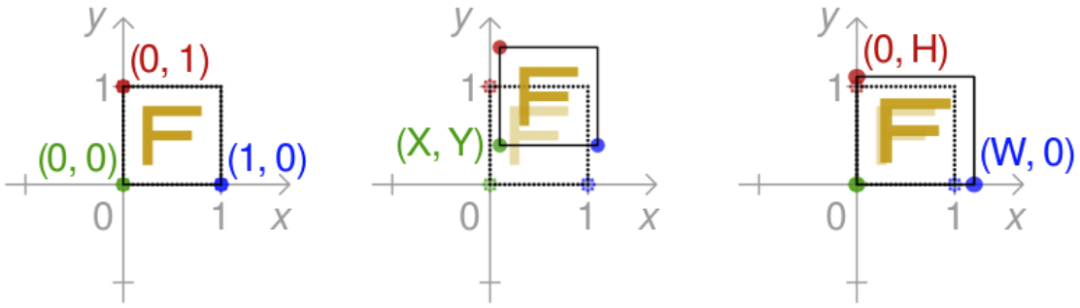
下图中，从左到右依次为恒等、平移和缩放变换。

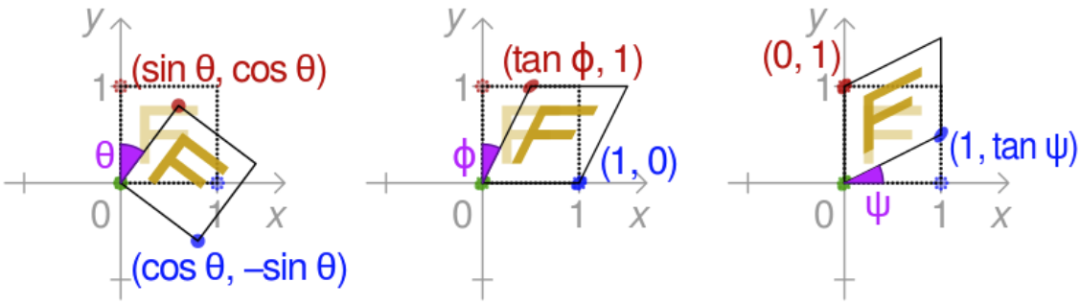
下图中，从左到右依次为旋转、水平方向错切和竖直方向错切变换。

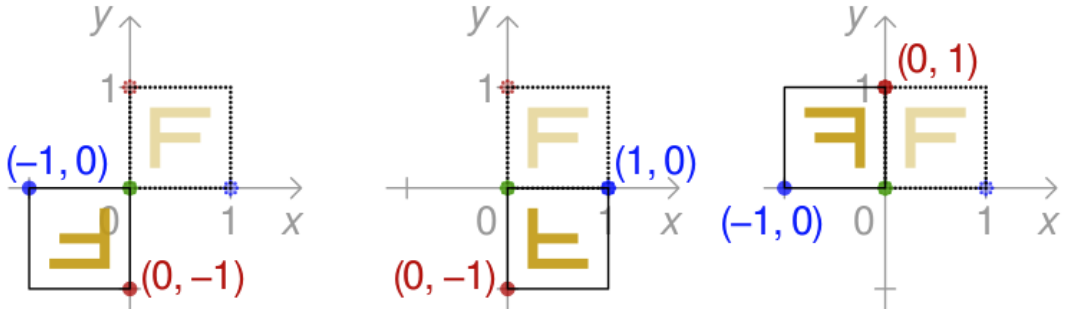
下图中，从左到右依次为水平和竖直两方向同时翻转、仅在竖直方向翻转以及仅在水平方向翻转映射。

非仿射变换举例

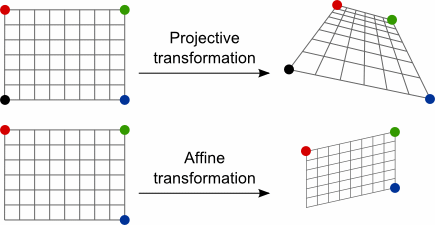
透视变换不是仿射变换，如上图所示，上面那行对应的是透视变换，它可能会改变同一条直线上各点间的比例，而下面那行对应的就是仿射变换。

局部仿射逼近

本文主要讨论使用雅可比矩阵来表示向量值函数的局部仿射逼近。由多元函数的泰勒展开可得，

我们把展开式中的高阶项省略掉，得到向量值函数的仿射逼近，

上式右边绿色框框里面的两项正是一个仿射映射。

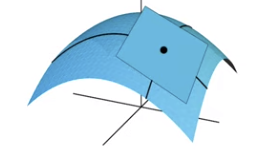
一般的函数 在点 处的附近区域不一定是线性的，不能用一个矩阵去精确表示它。但是，当这个局部非常小的时候，我们可以用一个仿射映射去近似逼近它。什么意思呢？就是站在点 处，各个方向走一小步 ，函数值 与函数值 的差 可以用步子 的一个线性变换来近似表示，即有

也就是说，用一个矩阵就可以去逼近表示函数的微小局部了。当然，每一点处的矩阵可能是不同的。那么这个矩阵具体是怎么样的呢？对，你已经看到过了，就是本文的主角，雅可比矩阵。

我们把雅可比矩阵，

代入下式（此处就直接用等号吧），

得，

多元向量值函数 在每个可微分的点处的导数或微分可以用一个矩阵表示，即所谓的雅可比矩阵。

导数怎么是一个矩阵呢？因为这是多元向量值函数的导数，跟一元数量函数的导数相比，在形式上自然应该有所升级。从形式上看有如下的关系，

• 一元数量函数的导数是一个数量，即斜率。

• 多元数量函数的导数是一个向量，即梯度。

• 多元向量值函数的导数是一个矩阵，即 Jacobian。

详细地说，如果 在 处是可微的， 是一个位移向量，表示定义域内的一小步，则矩阵-向量乘积  也是一个位移向量，用于近似表示 这一小步引起的函数在值域中的位移向量 ，即

这个映射将 附近的点  作如下映射，

它是对点  所在的微小区域的函数 的最佳仿射近似。

记住，该仿射映射中的线性部分的系数矩阵 称为 在 处的导数或微分。这个导数的写法有很多，在不同书上可能会看到这些记法，如 ，， 或者

而最后这个长得最臃肿的，有点接近雅可比当年写函数行列式时的记法。

3应用举例

雅可比行列式

当 时，雅可比矩阵为方阵，因此其行列式是有定义的，称为 的 雅可比行列式（Jacobian 行列式）。虽然它将 个数浓缩成了一个数，但它还算是精华的，包含了有关 的局部表现的重要信息。

例如，当且仅当雅可比行列式在 处不为零时，函数 在点 的局部具有反函数。如果为零，就会有分叉、降维啥的情况。

另外，如果结合雅可比矩阵的秩和特征值等，还可以揭示更多有用信息，后文再展开。

下面，让我们来看一看雅可比行列式在多元微积分中的应用。

坐标变换

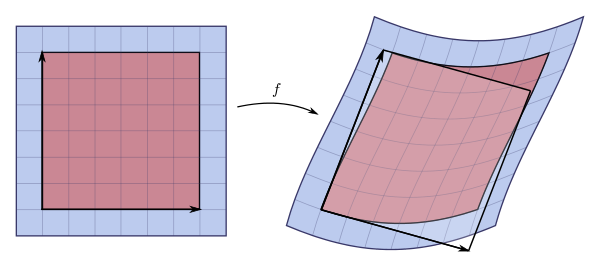
雅可比矩阵的一个用法是当 时，其行列式可用于坐标变换。

例如，在 笛卡尔坐标系上定义的数量函数 ，其在极坐标 中表示时变为 。

注意，这里考虑的函数 是数量函数，因此不是计算它的雅可比矩阵。这里要处理的多元向量值函数是指坐标间的变换，即映射 ，

此时，涉及的雅可比矩阵的行列式为 。

如果我们在直角坐标系区域 上考虑函数 的积分，则可以使用 Jacobian 行列式将其转换为极坐标上的积分，

这意味着无穷小面积 在 平面上并不均匀，并且取决于极坐标系上的 坐标值。

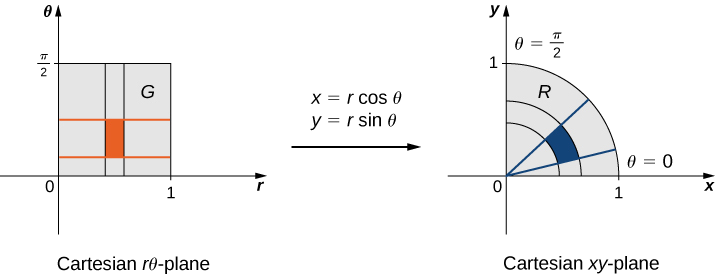
再看一个例子

，简单计算一下，可得此处的雅可比行列式为 ，因此有 。

直观解释

这里为什么要乘以雅可比行列式 呢？多元向量值函数、导数（雅可比矩阵）、行列式、多元微积分等这些概念怎么就凑一起了呢？其中有什么玄机呢？

接下来，我们并不想严格地用公式来证明这点，而是试图从比较直观的角度来解读这个现象。

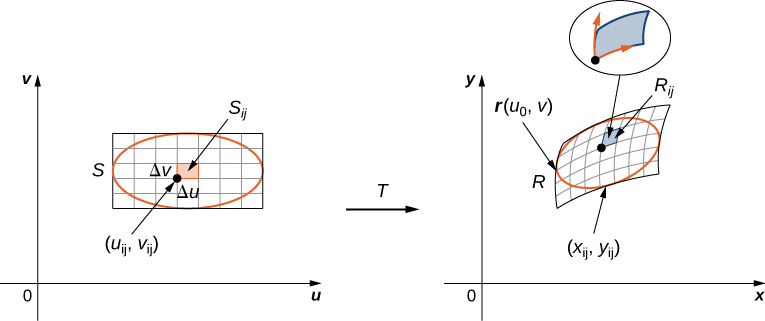
本系列文章中前面讲行列式的时候，已经提及过矩阵行列式的几何意义，是指变换前后面积的缩放倍数。

为了更清楚地揭示这一点，我们先对雅可比矩阵 作 分解，

其中，矩阵 和 都是正交矩阵，而 是对角矩阵。正交矩阵不改变向量的长度（向量的 范数），因此雅可比矩阵 对区域面积的改变主要体现在中间的对角矩阵，对角阵的对角线元素对应在各个坐标轴上的缩放倍数，它们的乘积就是整体面积的缩放倍数。而由柯西-比内公式可知，

再看坐标变换前后，对微小区域的面积可以作如下估计，

其中， 是求区域的面积， 是定义域中的小区域， 是变换后得到的小区域。这里用橙色小区域的仿射变换来逼近表示淡蓝色小区域，

需要注意的是，这里实际的向量值函数是 ，记得用它代替上文中局部仿射变换逼近公式中的 。

因此可得，

这就是雅可比行列式在多元微积分中的应用。可以直观地理解成，坐标变换引入了一个局部仿射变换，变换前后面积有缩放，缩放倍率正是雅可比矩阵的行列式。当然，这里只是直观地解释，并不是严格的证明。

方程求根之牛顿法

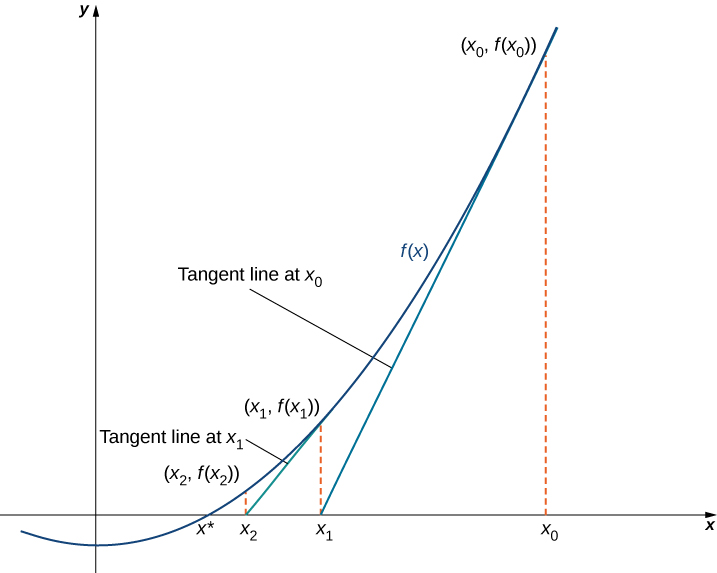
1、一元数量函数

我们可以使用牛顿法来计算 的根。假设根在 附近，为了找到更好的近似根 ，我们考虑如下 处的切线，

该切线与 轴的交点为 ，它揭示了比 更近的近似根。

因此，牛顿法的公式为

该方法的迭代过程如下图所示，实际操作中对初始值是有一定要求的。

2、多元数量函数

对于多元数量函数 ，假设 接近根，那么下式

是在点 处对函数 的仿射逼近，此时可以沿着梯度所在方向找更近似的根，可以令

代入上式，从而求得根的更新公式为

3、多元向量值函数

对于多元向量值函数 ，

计算 的根。

稍微一想，你会发现这个其实是在求解一个方程组的解，这里的方程一般来说是非线性的，当然也可以包括特例: 线性方程组。

如果是线性方程组，一般能一步到位；但如果是非线性的，往往不能一步到位，那就用迭代法一步一步逼近。假设 在根附近，该点处函数的仿射变换为，

其中，雅可比矩阵为，

如果 ，此时牛顿法的迭代公式为，

上面公式里要计算雅可比矩阵的逆，一般并不会直接去求，而是通过求解下面的方程组，

然后更新

这里所谓的迭代式求根方法的主要思路就是从当前的近似解如何得到更近似的解。

牛顿法就是利用函数局部的仿射逼近来一步一步逼近根。当然，具体实施中还需要处理初始值等一些细节问题。

另外，求解最优化问题也有牛顿法，而雅可比矩阵在最优化问题的求解方法中也会发挥作用，关于这些内容我们另外开篇再议。

4小结

本文首先了回顾雅可比矩阵的简短历史，然后是它的代表性用途: 可用于多元向量值函数的仿射逼近，最后举例说明在多元微积分坐标变换和牛顿法方程求根中的应用。

这么通俗地理解，我们可以用雅可比矩阵编码/刻画一个多元向量值函数的局部，从而简化分析函数的局部性质。

另外，雅可比矩阵是一条比较好的能够将多个内容串起来的线索。简单来看，它能将矩阵、仿射变换、行列式、特征值特征向量、导数、泰勒展开、微分方程组、方程求根、最优化甚至流形及其上的度量张量等等内容有机地牵扯起来。具体内容以及相关应用有待我们后续进一步展开。