AB 测试中的假设检验与分层抽样!(附代码和数据集)
今天由优秀的萝卜同学给大家分享一篇AB测试干货~
本文会将原理知识穿插于代码段中,相关代码和数据集空降文末可以获取。
前言
在电商网站 AB 测试非常常见,是将统计学与程序代码结合的经典案例之一。尽管如此,里面还是有许多值得学习和注意的地方。
A/B 测试用于测试网页的修改效果(浏览量,注册率等),测试需进行一场实验,实验中控制组为网页旧版本,实验组为网页新版本,实验还需选出一个指标 来衡量每组用户的参与度,然后根据实验结果来判断哪个版本效果更好。
通过这些测试,我们可以观察什么样的改动能最大化指标,测试适用的改动类型十分广泛,上到增加元素的大改动,下到颜色小变动都可使用这些测试。
背景
在本次案例研究中,我们将为教育平台 “ 不吹牛分析网 ” 分析 A/B 测试的结果,以下是该公司网站的客户漏斗模型:浏览主页 > 浏览课程概述页面(课程首页) > 注册课程 > 付费并完成课程
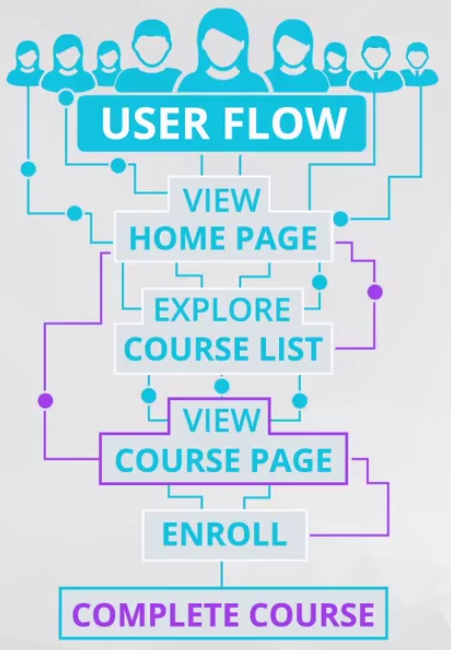
越深入漏斗模型,不吹牛分析网就会流失越多的用户(正常现象),能进入最后阶段的用户寥寥无几。为了提高参与度,提高每个阶段之间的转化率,z哥试着做出一些改动,并对改动进行了 A/B 测试,我们将帮z哥分析相关测试结果,并根据结果建议是否该实现页面改版。
因为利用 Python 进行 A/B 测试在每个数据集上的使用大同小异,所以我们这里只展示课程首页的A/B测试过程,其余页面的数据集会一并提供给大家作为练习。
Python实战
数据读入
import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport seaborn as snsplt.rc('font',**{'family':'Microsoft YaHei, SimHei'})# 设置中文字体的支持# 实现 notebook 的多行输出from IPython.core.interactiveshell import InteractiveShellInteractiveShell.ast_node_interactivity ='all' #默认为'last'course = pd.read_csv('course_page_actions.csv')course.info(); course.sample(5)
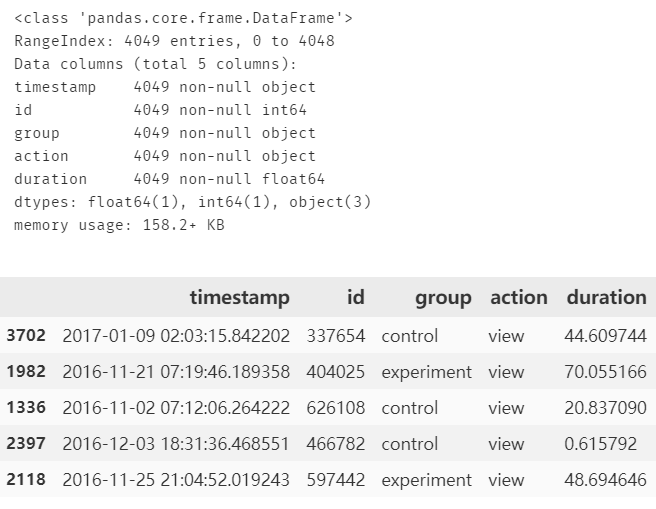
参数说明:
timestamp:浏览时间
id:用户 id
group:用户所属组别
action:用户行为,view--仅浏览;enroll--浏览并注册
duration:浏览界面时长(浏览越久,可能越感兴趣,就越有可能注册)
注册率分析
点击率 (CTR: click through rate)通常是点击数与浏览数的比例。因为网站页面会使用 cookies,所以我们可以确认单独用户,确保不重复统计同一个用户的点击率。为了进行该实验,我们对点击率作出如下定义:CTR: 单独用户点击数 / 单独用户浏览数,这一需要注意的点可以使用 pandas 中的 nunique() 函数来快捷完成

同理,实验组的计算方式相同,结果分析如下:

根据已有数据,我们通常会猜测会不会是新界面更加能够吸引用户停留并浏览,从而达到用户浏览时间越长,就越有可能注册课程
浏览时长分析
可视化分析
这里的我们将使用 seaborn 结合 markdown 公式的方式来实现快捷又强大的数据可视化
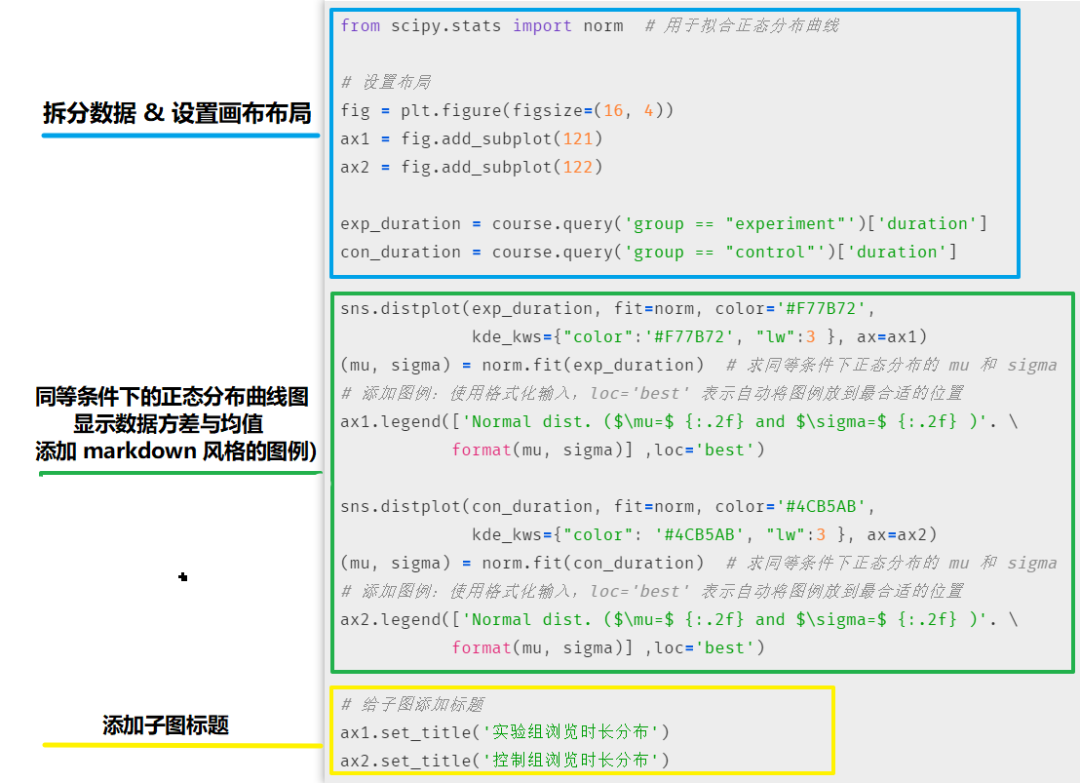

结果分析
新界面的注册率有所提高,而浏览时长方面均呈现轻微的右偏
实验组的浏览时长平均值比控制组高 15mins 左右,方差差别不大
所以我们可以初步判断新改版的课程首页更吸引用户,后续将进行假设检验来进一步验证我们的猜想
假设检验
我们将从控制组和实验组中各抽取一定数量的样本来进行假设检验,下面是置信水平 α 的选择经验:
样本量过大,α-level 就没什么意义了。为了使假设检验的数据样本更加合理,我们可以使用分层抽样。Python 没有现成的库或函数,可以使用前人的轮子。
from mysampling import get_sample# df: 输入的数据框 pandas.dataframe 对象# sampling:抽样方法 str## 可选值有 ["simple_random","stratified","systematic"]## 按顺序分别为: 简单随机抽样、分层抽样、系统抽样# stratified_col: 需要分层的列名的列表 list,只有在分层抽样时才生效# k: 抽样个数或抽样比例 int or float## (int, 则必须大于0; float,则必须在区间(0,1)中)## 如果 0< k <1, 则 k 表示抽样对于总体的比例## 如果 k >=1, 则 k 表示抽样的个数;当为分层抽样时,代表每层的样本量data =get_sample(df=course, sampling='stratified',stratified_col=['group'], k=300)data.sample(4); data.info()
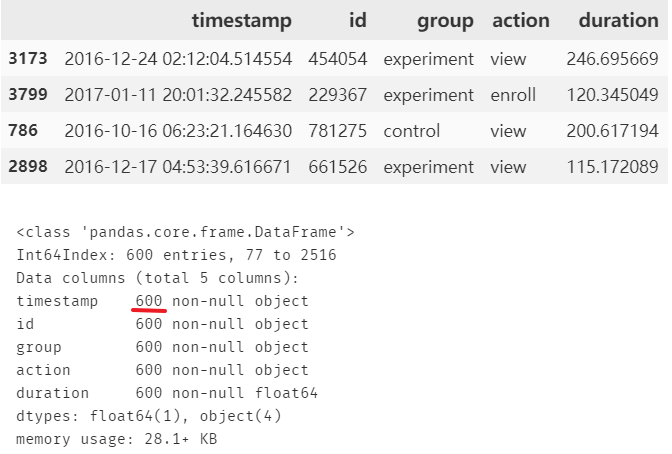
因为总体未知,所以我们可以使用两独立样本 T 检验,其实双样本 Z 检验也能达到类似的效果
# 总体未知,可采用两独立样本T检验from scipy import statsexp_duration = data.query('group == "experiment"')['duration']con_duration = data.query('group == "control"')['duration']print('两独立样本 T 检验...')stats.ttest_ind(a=exp_duration, b=con_duration)print('-'*45)print('双样本 Z 检验...')import statsmodels. api as smsm.stats.ztest(x1=exp_duration, x2=con_duration)
不难发现,有时双样本 Z 检验同样可以达到两独立样本 T 检验的效果。
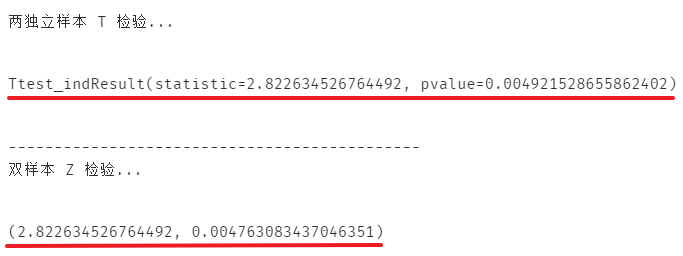
综述,我们将拒绝零假设,接受 “ 新界面的浏览时长显著不同于(高于)旧界面 ” 的这个假设。
AB测试的不足
但 A/B 测试也有不足之处。虽然测试能帮你比较两种选择,但无法告诉你你还没想到的选择,在对老用户进行测试时,抗拒改变心理、新奇效应等因素都可能使测试结果出现偏差。
抗拒改变心理:老用户可能会因为纯粹不喜欢改变而偏爱旧版本,哪怕从长远来看新版本更好。
新奇效应:老用户可能会觉得变化很新鲜,受变化吸引而偏爱新版本,哪怕从长远看来新版本并无益处。
所以在设计 A/B 测试、基于测试结果得出结论时都需要考虑诸多因素。下面总结了一些常见考虑因素:
老用户第一次体验改动会有新奇效应和改变抗拒心理;
要得到可靠的显著结果,需要有足够的流量和转化率;
要做出最佳决策,需选用最佳指标(如营收 vs 点击率);
应进行足够的实验时长,以便解释天/周/季度事件引起的行为变化;
转化率需具备现实指导意义(推出新元素的开支 vs 转化率提高带来的效益);
对照组和实验组的测试对象要有一致性(两组样本数失衡会造成辛普森悖论等现象的发生)。
完整案例数据和代码
链接:
https://pan.baidu.com/s/16GPrkrf4Bb6NAwOGInoEJA
提取码:v8bq
