大家好,我是陈锐。
今天分享内容来源Deephub Imba整理,仅供参考学习分享。
本文约3500字,建议阅读9分钟
本文对统计假设检验期间发生的 Type-I和 Type-II 错误的直观而详细的解释。
我们每天都在为选择进行自己的假设,并且按照自己认为最好的方向做出选择,所以假设在我们的生活中是无处不在的,例如:A 路是否会比 B 路花费更少的时间,X 的平均投资回报率是否高于 Y 的投资,以及电影 ABC 是否比电影 XYZ 好。在所有这些情况下,我们都在对我们做出的假设进行检验。建立假设,使用数据证明/反驳它们,帮助企业做出决策,这是数据科学家的实际工作。人们通常依靠概率来理解偶然观察数据的可能性,并利用它围绕假设得出结论。概率永远(几乎!)不会 100%,这反过来意味着我们永远无法 100% 确定我们的结论。所以在围绕我们假设的假设得出结论时,总是会出现错误的情况。下面的本文就是对统计假设检验期间发生的 Type-I和 Type-II 错误的直观而详细的解释。假设检验
假设检验是通过观察样本数据来检验围绕总体参数的假设的领域,因为我们很少有整体的数据,所以只能从整体中进行抽样观察。这通常是通过从假设的中性状态(称为原假设、零假设、虚无假设)开始并根据观察到的样本数据证明或反驳这一点来完成的。- 原假设 (H0) 是假设总体数据中的现状(无关系或无差异)的中性假设。
- H1 是 H0 的备选项,称为备择假设也被称为对立假设。
假设检验的基本思想是概率性质的反证法。根据所考察问题的要求提出原假设和备择假设,为了检验原假设是否正确,先假定原假设是正确的情况下,构造一个小概率事件,然后根据抽取的样本去检验这个小概率事件是否发生。假设 H0 → 观察样本数据 → 拒绝或不拒绝 H0我们假设中性 H0 为真,并在观察到的数据中寻找“拒绝”或“不拒绝”H0 的证据。根据观察到的样本数据,我们计算观察到的统计量和观察到的 P 值;例如:从我们观察到的样本中获得的假设 H0 为真的概率。然后将该观察到的 P 值与预先确定的显著性水平(或 Alpha 值)进行比较。此 Alpha 值充当阈值,超过该阈值会认为观察到的结果具有统计显着性。基于观察到的 P 值与预先选择的阈值 alpha 值的比较,就可以就假设的 H0 得出结论:- 观察到的 P 值 ≤ 预选 Alpha 级别 → 拒绝 H0
- 观察到的 P 值 > 预选的 Alpha 级别 → 不拒绝 H0
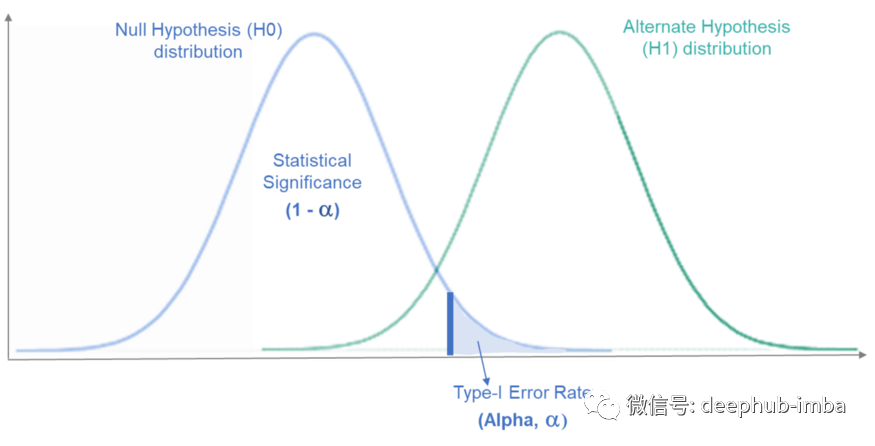
由于观察到的 P 值是一个概率,因此总是有可能对“拒绝”或“不拒绝”原假设做出错误的判断。在下图 1 中,左侧是假设的原假设 (H0) 总体分布,右侧是备择假设 (H1) 总体分布。(两者都是未知的和假设的,因为没有整体的数据,只是根据抽样的样本判断)。观察到的样本将位于这些分布的某个位置,基于此我们将得出关于我们的零假设 (H0) 的结论。如果分布没有重叠,我们将永远不会在结论中观察到错误。但是在实际情况中,它们几乎总是重叠的。Type-I 和 Type-II 错误发生在这两个分布重叠的地方。需要说明的是:对于原假设, 我们可以根据在数据中观察到的证据“拒绝它”,也可以“不拒绝它”,因为观察到的数据没有带来足够的重要证据。假设检验:可能性
实际上,H0 只有两个选项——它可以是 True 或 False。同样,根据观察到的数据,我们只能得出两个可能的结论——我们可以拒绝 H0 或不拒绝 H0。其实这就变成了一个二分类的问题,H0是正确的还是错误的
(2)和(3),我们正在根据观察到的数据做出正确的结论。(1)和 (4),我们得出了错误的结论,因为观察到的数据发现与现实背道而驰。在场景 (1) 和 (4) 中,就是本文要解释的 Type-I 和 Type-II 错误。如果你对统计学不了解,但是知道一些机器学习的理论的话,可以使用下面的类比方法:上面的1-4其实就是我们一直说的混淆矩阵,2,3是分类正确的值,即 TP 和 TN,1,4则是FP和FN。
Type-I 第一类错误
Type-I错误是指当原假设实际上为真时拒绝原假设的场景。根据我们观察到的数据得出结论是观察到的结果在现实中具有统计意,但是我们认为它是无意义的。如上所述,“拒绝”或“不拒绝”零假设取决于观察到的 P 值和预先确定的 alpha 值。所以在某些情况下,真实的原假设将被拒绝,因为观察到的 P 值将小于预先选择的 Alpha 水平。这就是Type-I错误的内容:False-Positive对于对总体正确的原假设,如果我们反复采样,可以得到原假设分布曲线,显示所有可能观察到的样本结果的概率。(下图2左侧H0分布)当我们观察一个样本时,我们拒绝 H0,这意味着这个观察到的样本必须位于 H0 分布曲线的最右侧,与 H1 分布曲线重叠。下图 2 表示这种情况:Type-I错误的区域,称为临界区域,表示在零假设分布曲线的右尾端。这是由我们预先选择的 Alpha 值决定的。如果我们观察到的结果落在这个区域,我们将拒绝零假设(对于这些场景,观察到的 p 值Type-II 第二类错误
Type-II错误是指当原假设实际上是错误的时不拒绝它的场景。根据我们观察到的数据得出的结论是,观察到的结果在实际上并不具有统计学意义,但是我们认为它是有意义的。Type-II错误:False-Negative这可能由于缺乏证据而发生,即我们的研究可能没有足够的统计能力来检测一定的效应大小。犯Type-II错误的概率用Beta 表示。统计研究的功效(Power )定义为,Power = 1 - Beta所以可以通过确保的研究具有较高的统计功效来减少犯Type-II错误的机会。对于对总体错误的零假设,如果我们反复从总体中抽取样本,我们将得到一条备择假设分布曲线,显示所有可能观察到的样本结果的概率。(下图3右侧H1分布)由于我们正在观察一个样本,因此我们没有证据拒绝 H0。这意味着这个观察到的样本必须位于 H1 分布曲线的最左侧,与 H0 分布曲线重叠(请参见下面的图3 代表这种情况)Beta 是 Type-II错误率,由左侧的阴影区域表示。右边的剩余区域代表统计功效(Power)。如果观察到的结果落在该区域内,将无法拒绝零假设,即使我们知道 H0 对于总体而言是错误的。所以得出一个False-Negative结论。几个例子
1、测试新药以帮助治疗疾病:H0新药无效、 H1新药有效- Type-I 错误 → 断定新药有效,但实际上无效。
- Type-II 错误 → 断定新药无效,而实际上它对治愈疾病有效。
- Type-I 错误 → 断定一个人是有罪的,而实际上他是无辜的。(即一个无辜的人被送进监狱)
- Type-II 错误 → 断定一个人是无辜的,但实际上他是有罪的。(即释放有罪的人)
I 和 II 错误之间的权衡
在假设检验中通过将观察值与预先确定的截止值 (Alpha) 进行比较来“拒绝”或“不拒绝”假设。所以考虑以下使 Alpha 越来越低的情况:情况1:如果 Alpha变得更严格(即 Alpha 的值越小),在拒绝 H0 方面的限制就会更严格,而在不拒绝 H0 方面的限制会更小。这会导致不太可能拒绝 H0,更有可能不拒绝 H0。- 在真实情况中 H0 为True的情况下,拒绝 H0 的可能性较小会导致Type-I错误比以前更少。
- 在真实情况中 H0 为 False 的情况下,更可能不拒绝 H0 将导致比以更多的 Type-II 错误。
情况2:如果 Alpha 级别变得不那么严格(即更高的 Alpha 值),在拒绝 H0 方面的限制将更少,而在不拒绝 H0 方面的限制更大。这会导致更有可能拒绝 H0,不太可能不拒绝 H0。- 在真实情况中 H0 为True的情况下,更有可能拒绝 H0 将导致以更多的 Type-I错误。
- 在真实情况中 H0 为 False 的情况下,不太可能不拒绝 H0 将导致Type-II错误比以前更少。
因此显然存在二者的权衡,因为2类的错误是相关的,当一个增加另一个减少时,反之亦然。从下图 4 可以看出,如果 Alpha 增加,则 Beta 减少,如果 Beta 减少,则 Alpha 将增加。图4:发生Type-I和 Type-II 错误的概率哪个类的错误更糟糕呢?没有简单的答案,因为都取决于被检验的假设和做出错误结论的成本评估:如果Type-I 的成本较高,则应尽量避免如果制作Type-II成本高,也应该优先考虑。但是通常认为Type-I误会产生更多后果,因为 Type-I错误意味着违背现状(H0)的假设,并可能导致引入新的变化,现有的状况产生更坏的影响。而 Type-II 错误意味着无法拒绝对现状 (H0) 的假设,并且可能只会导致错失机会。总结
假设检验是数据科学中一个非常重要的概念。统计的力量使我们能够对总体做出假设,观察数据样本以使我们能够拒绝或不拒绝我们的假设并得出结论。假设检验有两种可能的错误——Type-I错误和Type-II错误。假设检验过程:假设一个中性 H0 → 观察数据(将观察到的 P 值与预先确定的 alpha 水平进行比较)→ 拒绝或不拒绝 H0。Type-I错误:False-Positive
Type-II错误:False-Negative
Type-I 和 Type-II 错误相互影响相反。减少一个总是增加另一个,反之亦然。一般来说,Type-I 错误被认为Type-II 错误更重要。但是,也要取决于被检验的假设以及围绕我们的假设得出这些错误结论的成本。本文仅供学习参考,不作其它用途,有任何疑问及侵权,扫描以下公众号二维码添加交流:
更多学习内容,仅在知识星球发布: