Kaggle 案例精选 - 附数据和代码

数据表明越来越多的客户放弃使用信用卡，这让银行客户经理们感到不安。如果能预测哪些客户将会流失，他们将会主动向相关客户提供更好的服务，从而挽留客户。

该数据集由 10,000 个客户组成，其中包含年龄、工资、婚姻状况、信用卡限额、信用卡类别等 18 个特征。

数据集中只有 16.07％ 的客户流失，因此类别不平衡，这让训练模型来预测客户流失带来一定困难。该怎么办呢？

0
目录

1. 简介

• 1.1 库和实用程序
• 1.2 数据加载

2. 探索性数据分析（EDA）

3. 数据预处理

• 3.1 使用 SMOTE 对数据上采样
• 3.2 基于独热编码的主成分分析

4. 选型与评估

• 4.1 交叉验证
• 4.2 模型评估
• 4.3 原始数据上的模型评估

5. 结果

1简介

.1.1库和实用程序

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.express as ex
import plotly.graph_objs as go
import plotly.figure_factory as ff
from plotly.subplots import make_subplots
import plotly.offline as pyo
pyo.init_notebook_mode()
sns.set_style('darkgrid')
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split,cross_val_score
from sklearn.ensemble import RandomForestClassifier,AdaBoostClassifier
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import f1_score as f1
from sklearn.metrics import confusion_matrix
import scikitplot as skplt

plt.rc('figure',figsize=(18,9))
%pip install imbalanced-learn
from imblearn.over_sampling import SMOTE

.1.2数据加载

c_data = pd.read_csv('./input/credit-card-customers/BankChurners.csv')
c_data = c_data[c_data.columns[:-2]]
c_data.head(3)

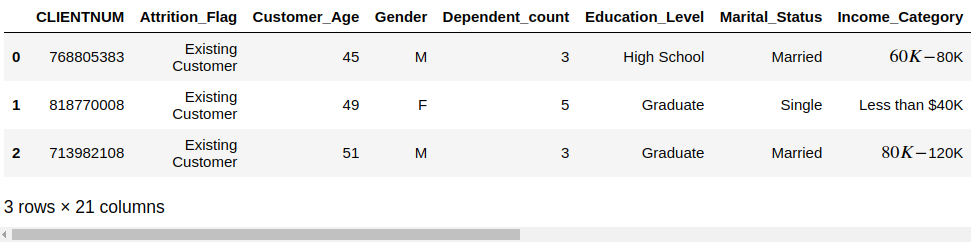
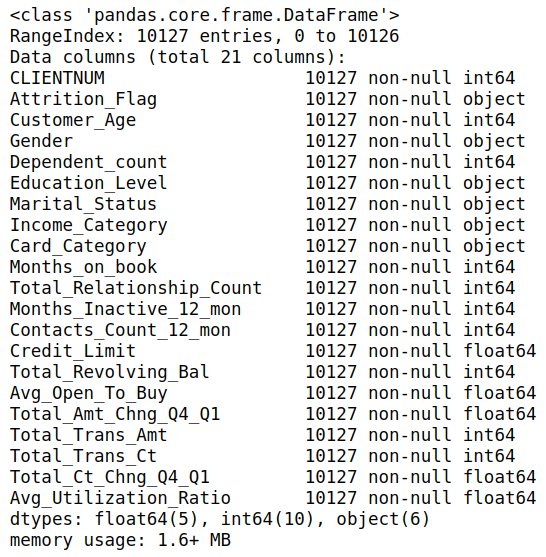
总共有 21 列，下面查看各属性的总体情况，数据类型是否有缺失值等。

c_data.info()

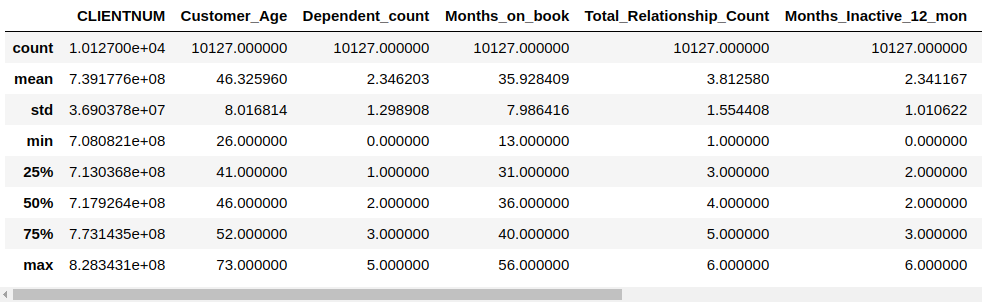
# 查看数值型特征的统计信息
c_data.describe()

2探索性数据分析

客户年龄分布

# Distribution of Customer Ages
fig = make_subplots(rows=2, cols=1)

tr1=go.Box(x=c_data['Customer_Age'],name='Age Box Plot',boxmean=True)
tr2=go.Histogram(x=c_data['Customer_Age'],name='Age Histogram')

fig.add_trace(tr1,row=1,col=1)
fig.add_trace(tr2,row=2,col=1)

fig.update_layout(height=600, width=900, title_text="客户年龄分布")
fig.show()

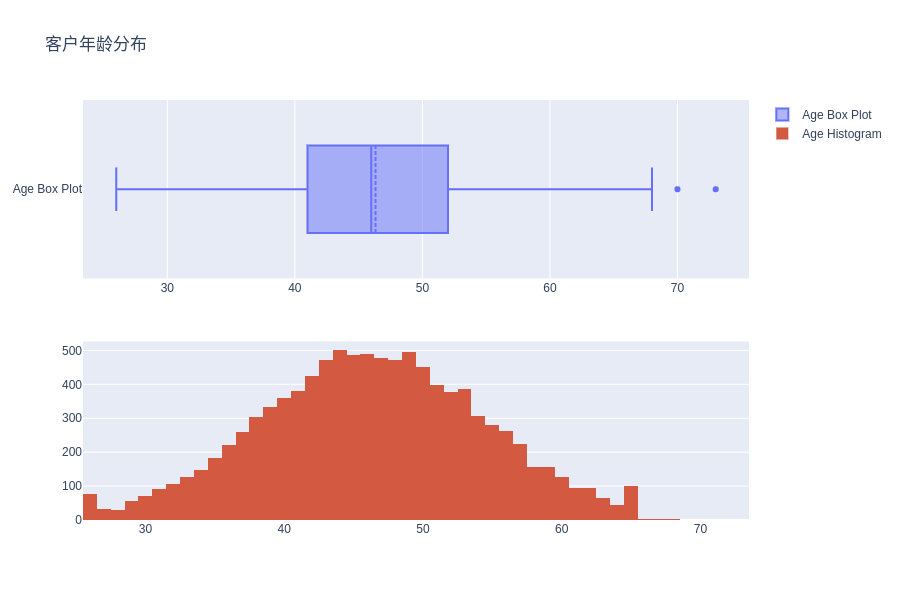
可以看到，该数据集中的客户年龄服从正态分布，因此在后续处理中可以使用正态性假设来使用年龄这个特征。

客户性别比例

# Propotion Of Customer Genders
ex.pie(c_data, names='Gender', title='客户性别比例')

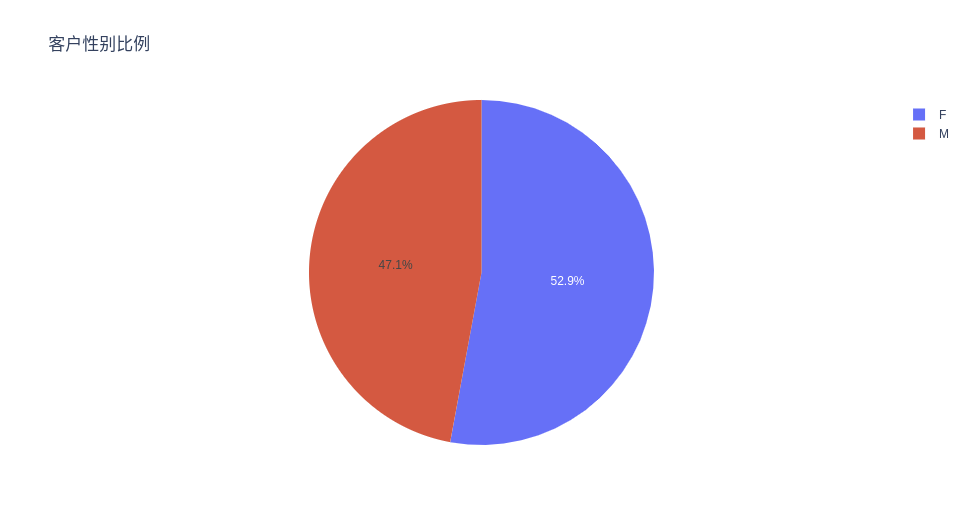
与男性相比，该数据集中有更多的女性客户，但差异并不显着，因此可以说性别是均匀分布的。

客户家庭人数分布

# Distribution of Dependent counts (close family size)
fig = make_subplots(rows=2, cols=1)

tr1=go.Box(x=c_data['Dependent_count'], name='Dependent count Box Plot',boxmean=True)
tr2=go.Histogram(x=c_data['Dependent_count'], name='Dependent count Histogram')

fig.add_trace(tr1,row=1,col=1)
fig.add_trace(tr2,row=2,col=1)

fig.update_layout(height=600, width=900, title_text="客户家庭人数分布")
fig.show()

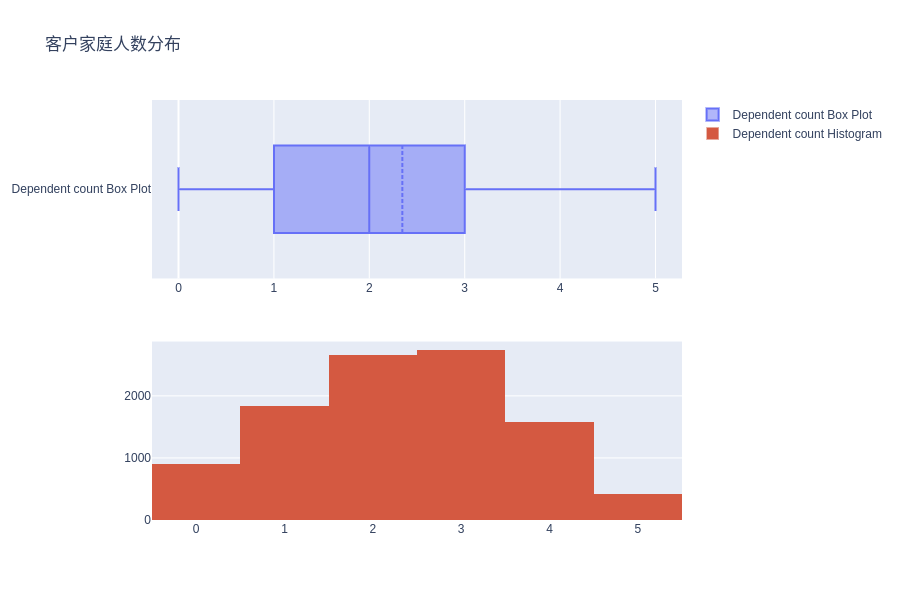
客户家庭人数的分布近似服从正态分布，偏度略小于 0。

print('Skewness of Dependent_count is : {}'.format(c_data['Dependent_count'].skew()))

受教育程度比例

# Propotion Of Education Levels
ex.pie(c_data, names='Education_Level', title='受教育程度比例')

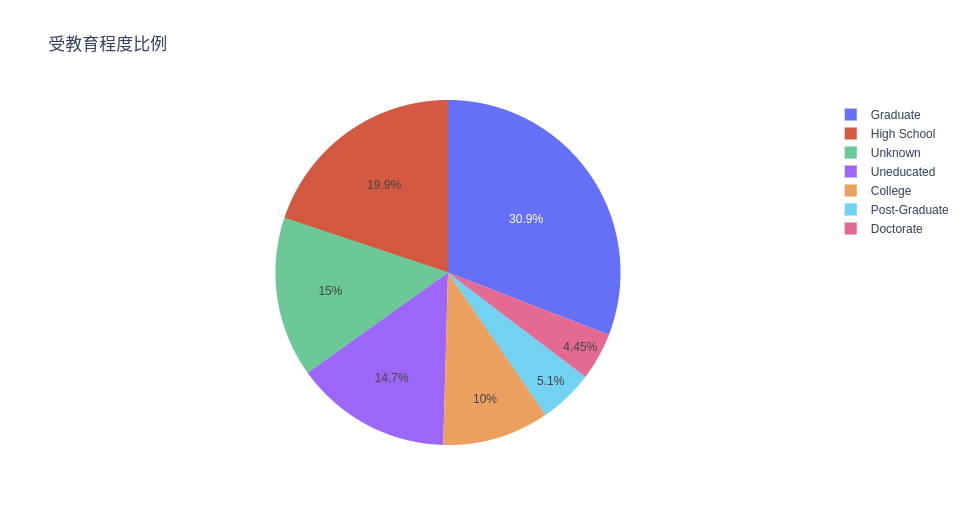
可以看到，超过 70％ 的客户受过正规教育，其中约 35％ 的客户具有较高的教育水平。

婚姻状况比例

# Propotion Of Different Marriage Statuses
ex.pie(c_data, names='Marital_Status', title='婚姻状况比例')

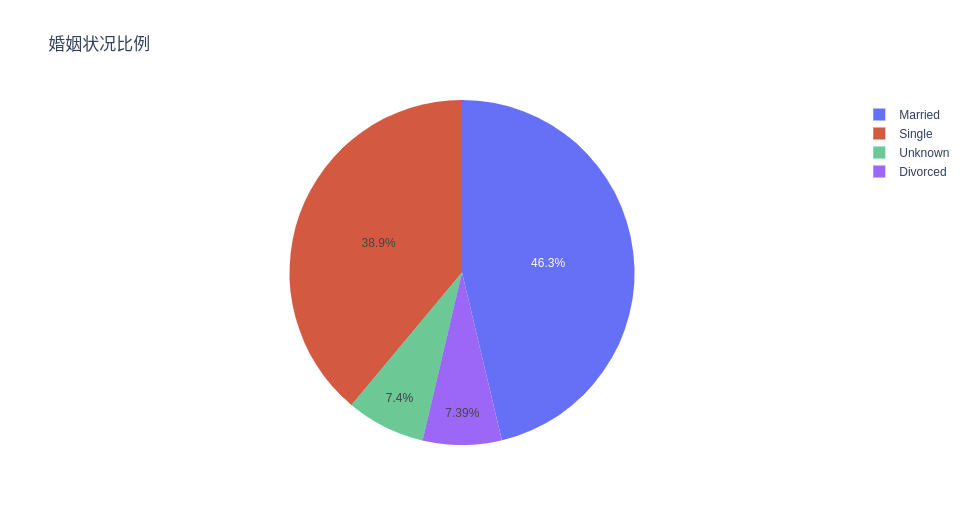
银行近一半的客户已婚，有趣的是，几乎另一半的客户都是单身客户。离婚率只有 7％ 左右，考虑到全球离婚率统计，这多少有点令人惊讶呀！

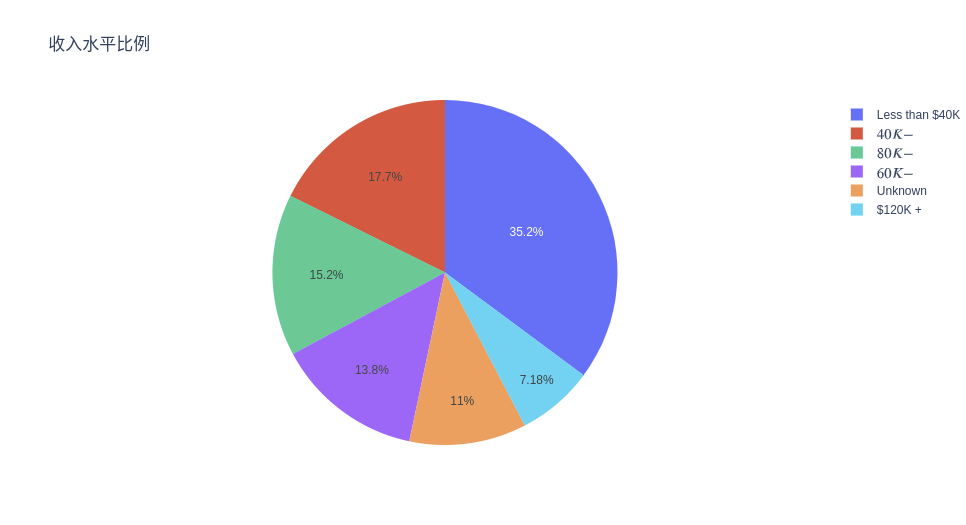
收入水平比例

# Propotion Of Different Income Levels
ex.pie(c_data, names='Income_Category', title='收入水平比例')

信用卡类别比例

# Propotion Of Different Card Categories
ex.pie(c_data, names='Card_Category', title='信用卡类别比例')

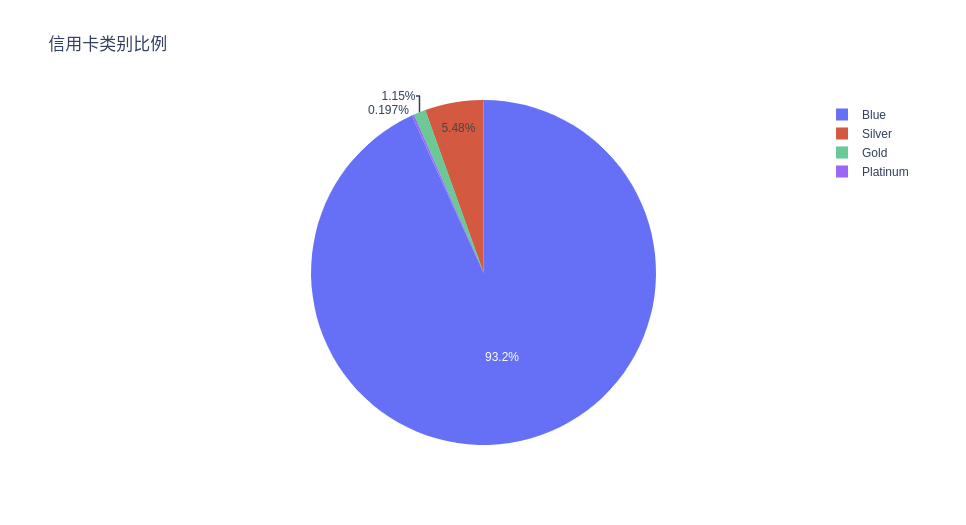
可以看到绝大多数客户办的是蓝卡。

客户加入银行会员的时间（月份）分布

# Distribution of months the customer is part of the bank
fig = make_subplots(rows=2, cols=1)

tr1=go.Box(x=c_data['Months_on_book'], name='Months on book Box Plot',boxmean=True)
tr2=go.Histogram(x=c_data['Months_on_book'], name='客户加入银行会员的时间（月份）分布')

fig.add_trace(tr1,row=1,col=1)
fig.add_trace(tr2,row=2,col=1)

fig.update_layout(height=600, width=900, title_text="客户加入银行会员的时间（月份）分布")
fig.show()

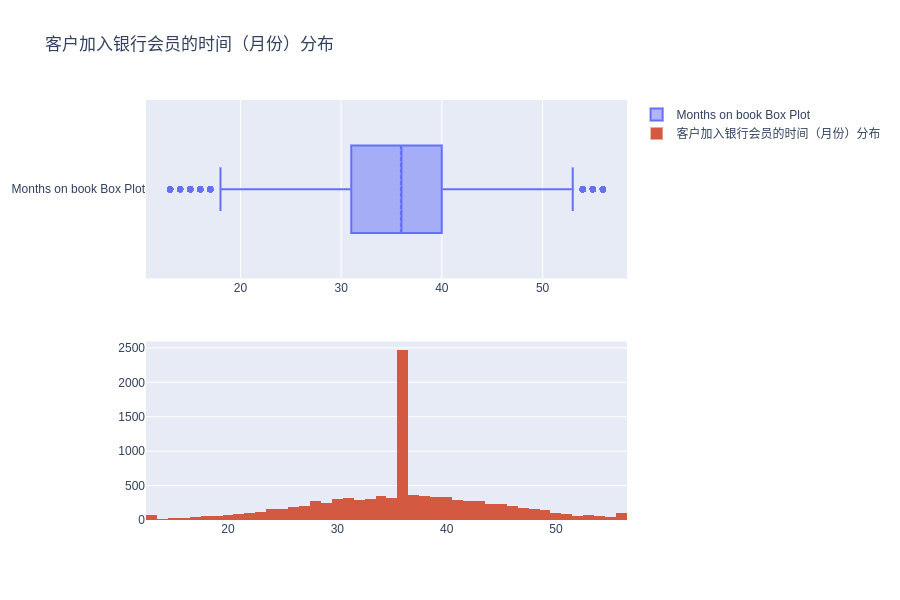
print('Kurtosis of Months on book features is : {}'.format(c_data['Months_on_book'].kurt()))

峰度值（0.40）很低，指向非常平坦的形状分布（也可以在上面的图中看到），这意味着我们无法假定特征的正态性。

峰度（kurtosis），是和正态分布相比较而言的统计量，直观地反映了峰部的尖度。一般来说，峰度大于 3，峰的形状比较尖，比正态分布峰要陡峭。

客户持有的产品数量分布

# Distribution of Total no. of products held by the customer
fig = make_subplots(rows=2, cols=1)

tr1 = go.Box(x=c_data['Total_Relationship_Count'], name='Total no. of products Box Plot',boxmean=True)
tr2 = go.Histogram(x=c_data['Total_Relationship_Count'], name='Total no. of products Histogram')

fig.add_trace(tr1, row=1, col=1)
fig.add_trace(tr2, row=2, col=1)

fig.update_layout(height=600, width=900, title_text="客户持有的产品数量分布")
fig.show()

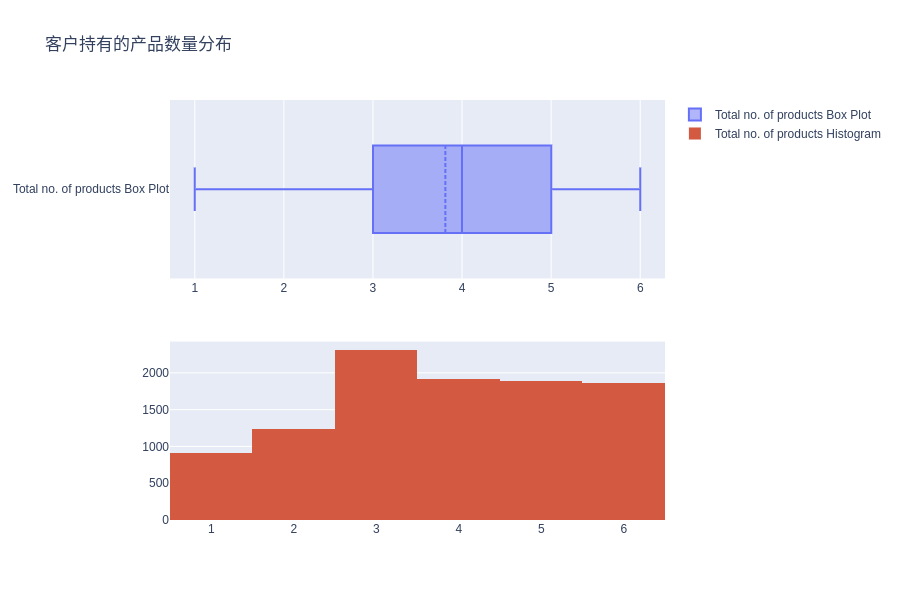
客户持有的产品总数的分布似乎更接近于均匀分布，因此对于预测客户流失状况可能并没有啥用处。

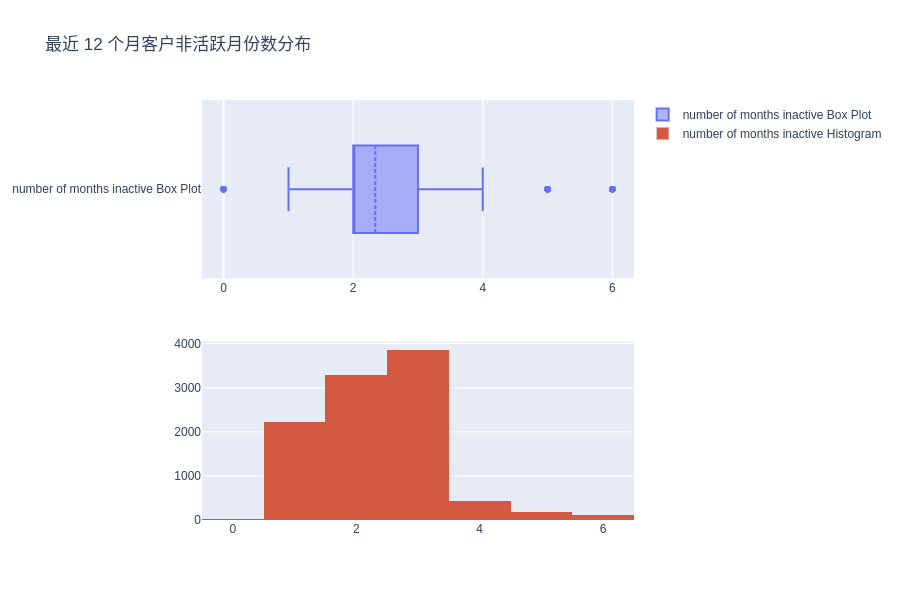
最近 12 个月客户非活跃月份数分布

# Distribution of the number of months inactive in the last 12 months
fig = make_subplots(rows=2, cols=1)

tr1=go.Box(x=c_data['Months_Inactive_12_mon'],name='number of months inactive Box Plot',boxmean=True)
tr2=go.Histogram(x=c_data['Months_Inactive_12_mon'],name='number of months inactive Histogram')

fig.add_trace(tr1,row=1,col=1)
fig.add_trace(tr2,row=2,col=1)

fig.update_layout(height=600, width=900, title_text="最近 12 个月客户非活跃月份数分布")
fig.show()

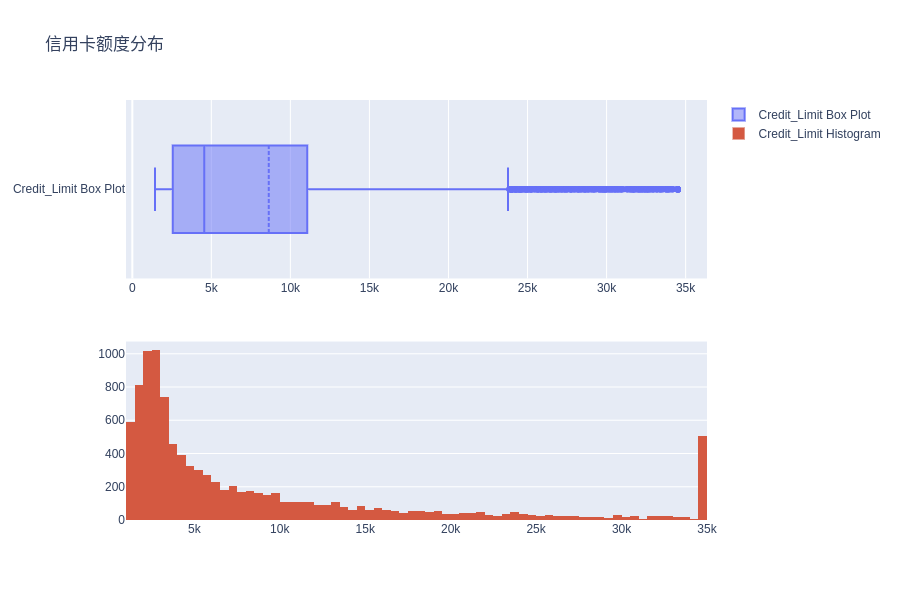
信用卡额度分布

fig = make_subplots(rows=2, cols=1)

tr1=go.Box(x=c_data['Credit_Limit'], name='Credit_Limit Box Plot', boxmean=True)
tr2=go.Histogram(x=c_data['Credit_Limit'], name='Credit_Limit Histogram')

fig.add_trace(tr1, row=1, col=1)
fig.add_trace(tr2, row=2, col=1)

fig.update_layout(height=600, width=900, title_text="信用卡额度分布")
fig.show()

过去 12 个月总交易金额分布

# Distribution of the Total Transaction Amount (Last 12 months)
fig = make_subplots(rows=2, cols=1)

tr1=go.Box(x=c_data['Total_Trans_Amt'], name='Total_Trans_Amt Box Plot', boxmean=True)
tr2=go.Histogram(x=c_data['Total_Trans_Amt'], name='Total_Trans_Amt Histogram')

fig.add_trace(tr1,row=1,col=1)
fig.add_trace(tr2,row=2,col=1)

fig.update_layout(height=600, width=900, title_text="过去 12 个月总交易金额分布")
fig.show()

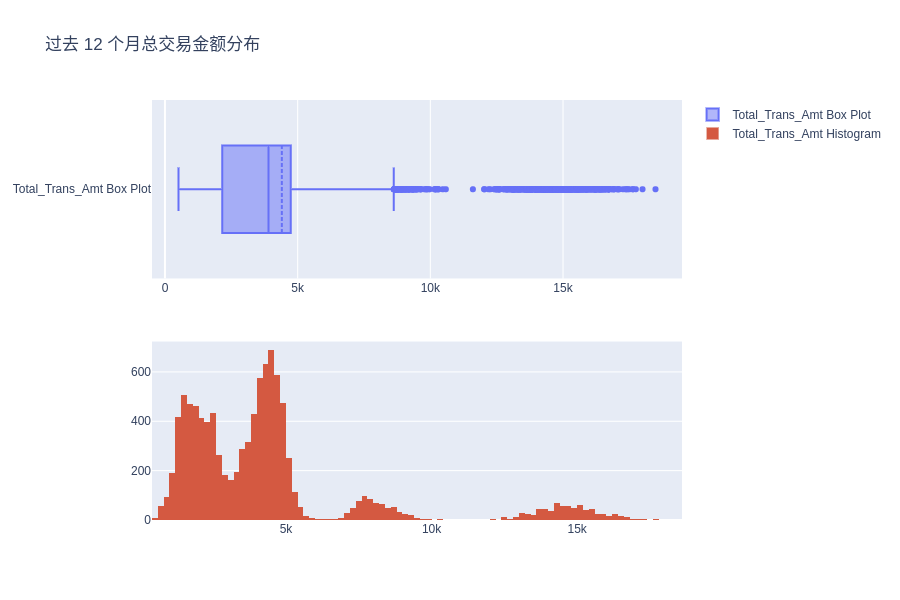
可以看到，过去 12 个月的总交易分布显示出了多个波峰，这意味着该数据中存在一些潜在的组别。

尝试对不同的组别进行聚类、查看它们之间的相似性以及如何更好地描述在数据分布中形成不同模式的不同群体等将是一个非常有趣的实验。

流失客户与非流失客户的比例

ex.pie(c_data, names='Attrition_Flag', title='流失客户占比')

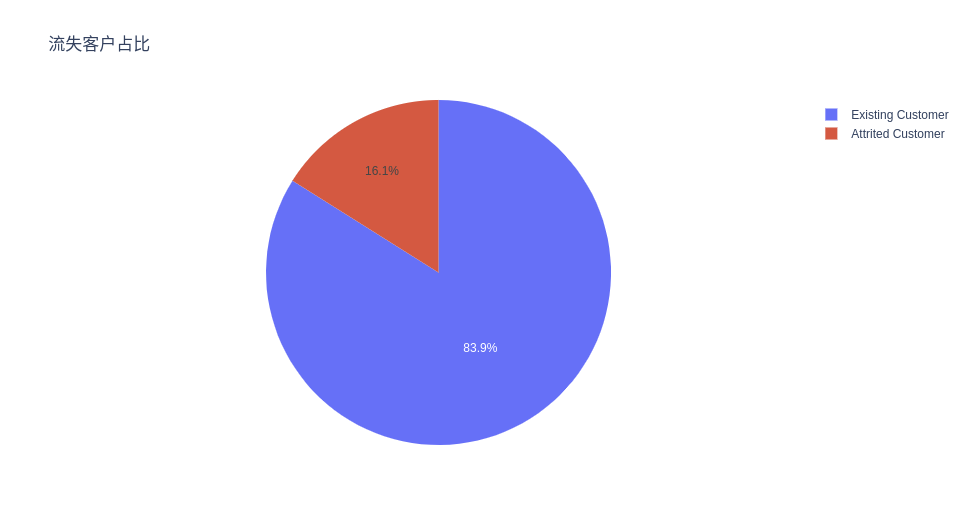
正如我们看到的那样，只有 16％ 的数据样本代表流失客户，在比例上看，这属于类别不平衡数据。直接在该数据上训练模型，会使得模型很难捕捉到小类别上的特征。

因此，在后续步骤中，我将使用 SMOTE 包对流失客户样本进行上采样，以使得其数量与常规客户样本数量相当，从而让后续模型更好地学习。

3数据预处理

c_data.Attrition_Flag = c_data.Attrition_Flag.replace({'Attrited Customer':1,'Existing Customer':0})
c_data.Gender = c_data.Gender.replace({'F':1,'M':0})
c_data = pd.concat([c_data,pd.get_dummies(c_data['Education_Level']).drop(columns=['Unknown'])], axis=1)
c_data = pd.concat([c_data,pd.get_dummies(c_data['Income_Category']).drop(columns=['Unknown'])], axis=1)
c_data = pd.concat([c_data,pd.get_dummies(c_data['Marital_Status']).drop(columns=['Unknown'])], axis=1)
c_data = pd.concat([c_data,pd.get_dummies(c_data['Card_Category']).drop(columns=['Platinum'])], axis=1)
c_data.drop(columns = ['Education_Level','Income_Category','Marital_Status','Card_Category','CLIENTNUM'], inplace=True)

# 展示独热编码后的特征，是不是多了几列啦
c_data.info()

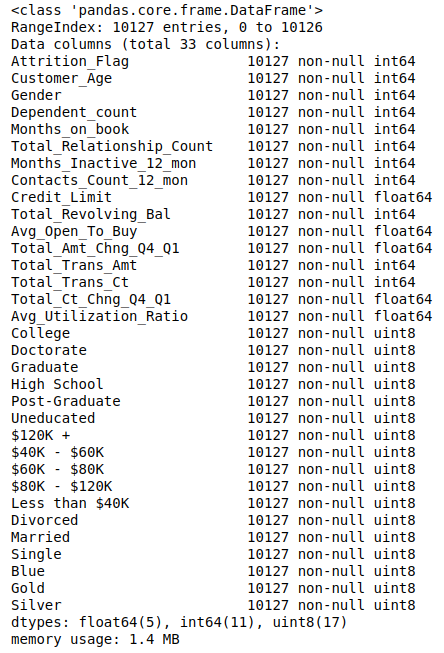
上面代码对所有描述客户不同状态的类别特征进行独热编码。

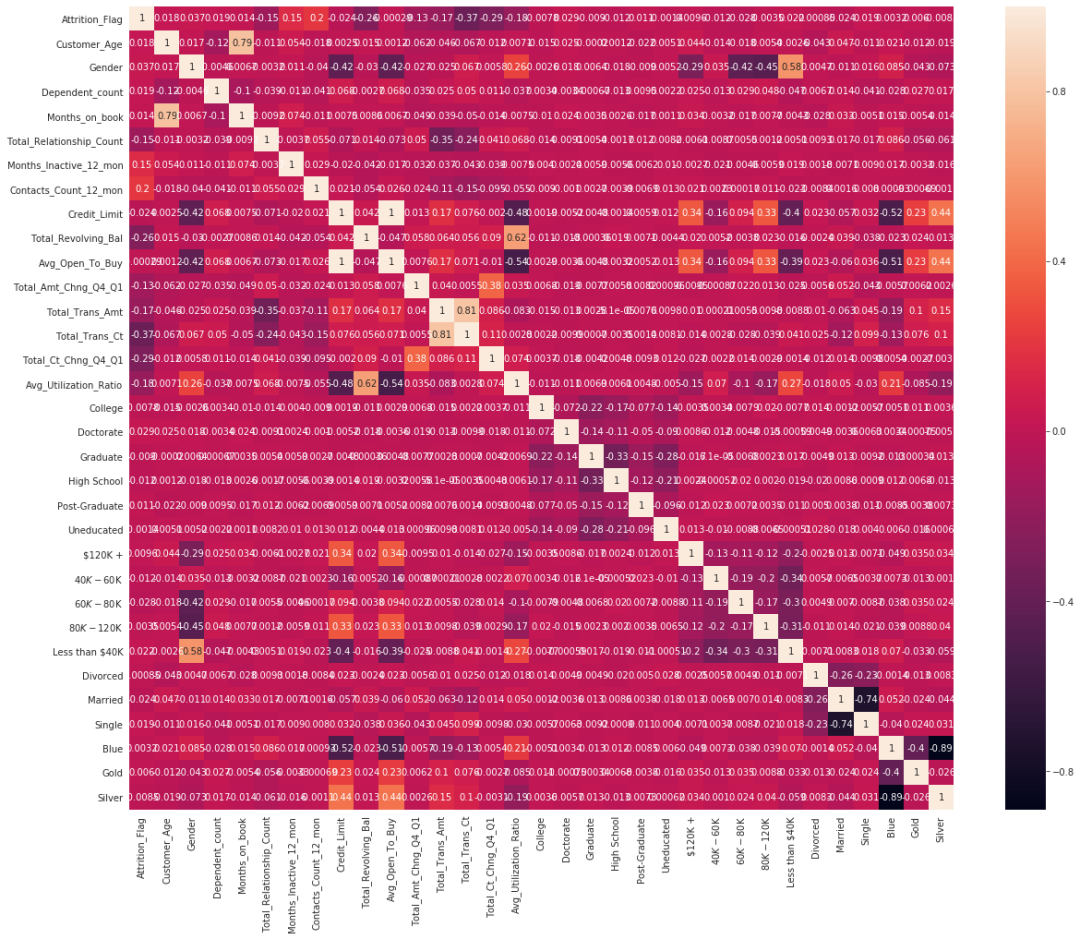
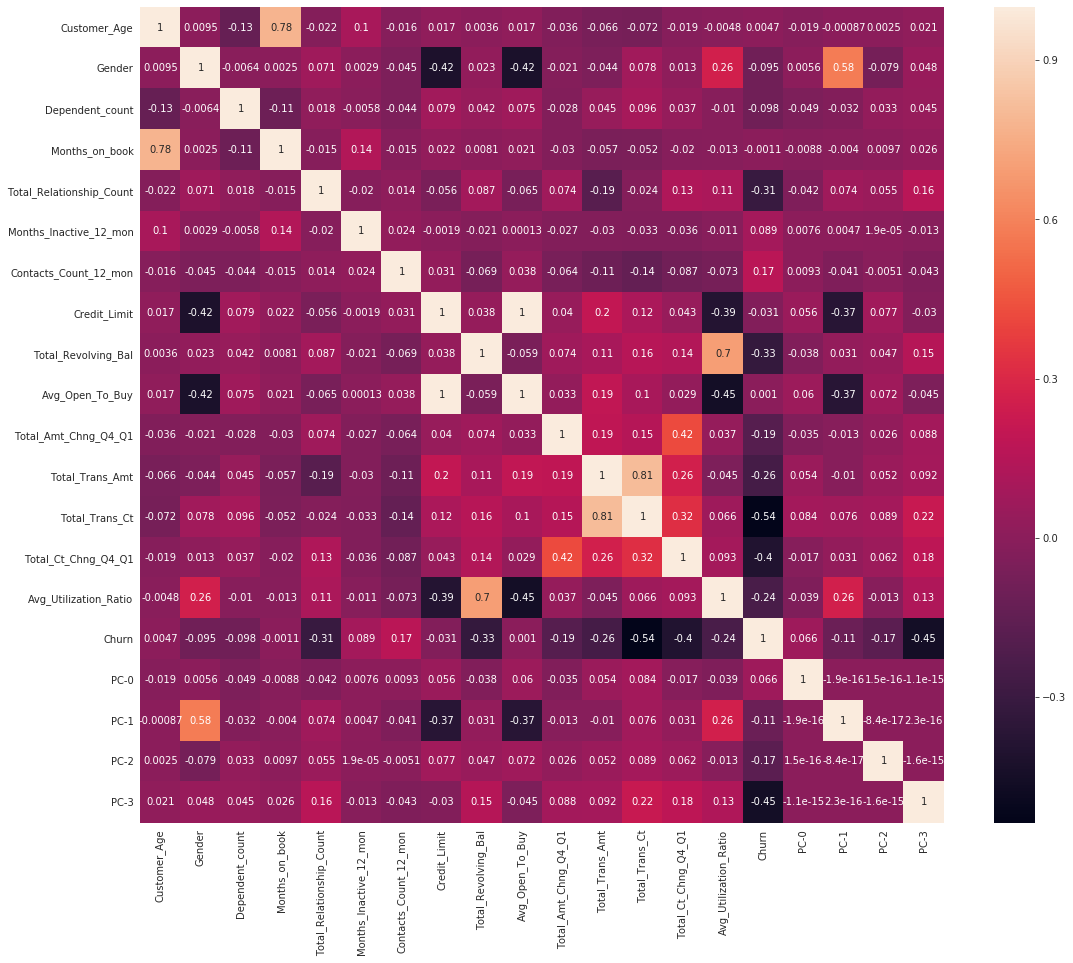
下面代码计算各个特征间的相关系数并用热图可视化。

plt.figure(figsize=(20, 16))
ax = sns.heatmap(c_data.corr('pearson'), annot=True);
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)

.3.1使用 SMOTE 对数据上采样

oversample = SMOTE()
X, y = oversample.fit_resample(c_data[c_data.columns[1:]], c_data[c_data.columns[0]])
usampled_df = X.assign(Churn = y)

ohe_data =usampled_df[usampled_df.columns[15:-1]].copy()

usampled_df = usampled_df.drop(columns=usampled_df.columns[15:-1])

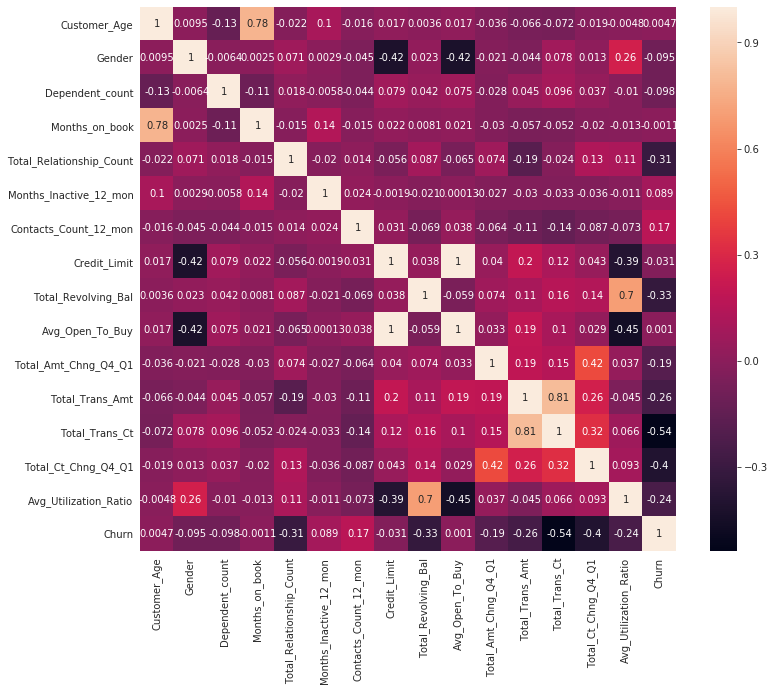
plt.figure(figsize=(12, 10))
ax = sns.heatmap(usampled_df.corr('pearson'),annot=True)
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)

.3.2独热编码数据的主成分分析

我们将使用主成分分析（PCA）来对独热编码的分类变量进行降维，仅仅使用几个主成分而不是数十个独热编码的特征，这对于更好地构建后续模型非常有帮助。

N_COMPONENTS = 4

pca_model = PCA(n_components = N_COMPONENTS )

pc_matrix = pca_model.fit_transform(ohe_data)

evr = pca_model.explained_variance_ratio_
cumsum_evr = np.cumsum(evr)

plt.figure(figsize=(12, 6))
ax = sns.lineplot(x=np.arange(0,len(cumsum_evr)),y=cumsum_evr,label='Explained Variance Ratio')
ax.lines[0].set_linestyle('-.')
ax.set_title('Explained Variance Ratio Using {} Components'.format(N_COMPONENTS))
ax.plot(np.arange(0,len(cumsum_evr)),cumsum_evr,'bo')
ax = sns.lineplot(x=np.arange(0,len(cumsum_evr)),y=evr,label='Explained Variance Of Component X')
ax.plot(np.arange(0,len(evr)),evr,'ro')
ax.lines[1].set_linestyle('-.')
ax.set_xticks([i for i in range(0,len(cumsum_evr))])
ax.set_xlabel('Component number #')
ax.set_ylabel('Explained Variance')
plt.show()

上面展示的 Explained Variance Ratio 表示降维后的各主成分的方差值占方差总和的比例，保留的维度越多，这个比例自然越大。

usampled_df_with_pcs = pd.concat([usampled_df,pd.DataFrame(pc_matrix,columns=['PC-{}'.format(i) for i in range(0,N_COMPONENTS)])],axis=1)
usampled_df_with_pcs

# 再次计算相关系数
plt.figure(figsize=(18, 15))
ax = sns.heatmap(usampled_df_with_pcs.corr('pearson'), annot=True)
bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)

4模型选择和评估

从上面的相关系数热图里挑出几个与目标列之间的相关系数较大的列作为最终的特征。

X_features = ['Total_Trans_Ct','PC-3','PC-1','PC-0','PC-2','Total_Ct_Chng_Q4_Q1','Total_Relationship_Count']

X = usampled_df_with_pcs[X_features]
y = usampled_df_with_pcs['Churn']

X.shape

# 划分数据集
train_x,test_x,train_y,test_y = train_test_split(X, y, random_state=10)

.4.1交叉验证

rf_pipe = Pipeline(steps =[ ('scale',StandardScaler()), ("RF",RandomForestClassifier(random_state=10)) ])
ada_pipe = Pipeline(steps =[ ('scale',StandardScaler()), ("RF",AdaBoostClassifier(random_state=10,learning_rate=0.7)) ])
svm_pipe = Pipeline(steps =[ ('scale',StandardScaler()), ("RF",SVC(random_state=10,kernel='rbf')) ])


f1_cross_val_scores = cross_val_score(rf_pipe,train_x,train_y,cv=5,scoring='f1')
ada_f1_cross_val_scores = cross_val_score(ada_pipe,train_x,train_y,cv=5,scoring='f1')
svm_f1_cross_val_scores = cross_val_score(svm_pipe,train_x,train_y,cv=5,scoring='f1')

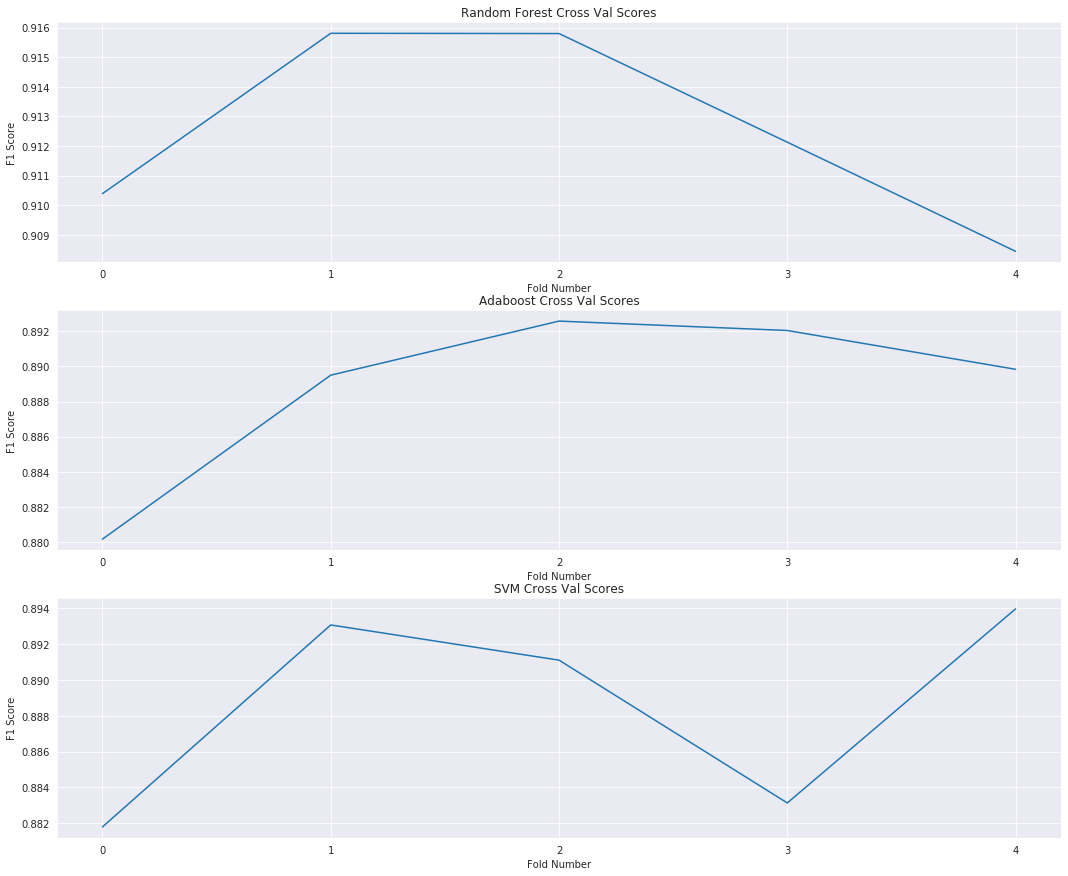
plt.figure(figsize=(18, 15))
plt.subplot(3,1,1)
ax = sns.lineplot(x=range(0,len(f1_cross_val_scores)),y=f1_cross_val_scores)
ax.set_title('Random Forest Cross Val Scores')
ax.set_xticks([i for i in range(0,len(f1_cross_val_scores))])
ax.set_xlabel('Fold Number')
ax.set_ylabel('F1 Score')

plt.subplot(3,1,2)
ax = sns.lineplot(x=range(0,len(ada_f1_cross_val_scores)),y=ada_f1_cross_val_scores)
ax.set_title('Adaboost Cross Val Scores')
ax.set_xticks([i for i in range(0,len(ada_f1_cross_val_scores))])
ax.set_xlabel('Fold Number')
ax.set_ylabel('F1 Score')

plt.subplot(3,1,3)
ax = sns.lineplot(x=range(0,len(svm_f1_cross_val_scores)),y=svm_f1_cross_val_scores)
ax.set_title('SVM Cross Val Scores')
ax.set_xticks([i for i in range(0,len(svm_f1_cross_val_scores))])
ax.set_xlabel('Fold Number')
ax.set_ylabel('F1 Score')
plt.show()

.4.2模型评估

rf_pipe.fit(train_x,train_y)
rf_prediction = rf_pipe.predict(test_x)

ada_pipe.fit(train_x,train_y)
ada_prediction = ada_pipe.predict(test_x)

svm_pipe.fit(train_x,train_y)
svm_prediction = svm_pipe.predict(test_x)

print('F1 Score of Random Forest Model On Test Set - {}'.format(f1(rf_prediction,test_y)))
print('F1 Score of AdaBoost Model On Test Set - {}'.format(f1(ada_prediction,test_y)))
print('F1 Score of SVM Model On Test Set - {}'.format(f1(svm_prediction,test_y)))

F1 Score of RF Model - 0.910253374378404
F1 Score of AdaBoost - 0.882673619341076
F1 Score of SVM Model - 0.8902119552274351

.4.3原始数据上的模型评估

ohe_data =c_data[c_data.columns[16:]].copy()
pc_matrix = pca_model.fit_transform(ohe_data)
original_df_with_pcs = pd.concat([c_data,pd.DataFrame(pc_matrix,columns=['PC-{}'.format(i) for i in range(0,N_COMPONENTS)])],axis=1)

unsampled_data_prediction_RF = rf_pipe.predict(original_df_with_pcs[X_features])
unsampled_data_prediction_ADA = ada_pipe.predict(original_df_with_pcs[X_features])
unsampled_data_prediction_SVM = svm_pipe.predict(original_df_with_pcs[X_features])

print('F1 Score of Random Forest Model On Original Data (Before Upsampling) - {}'.format(f1(unsampled_data_prediction_RF,original_df_with_pcs['Attrition_Flag'])))
print('F1 Score of AdaBoost Model On Original Data (Before Upsampling) - {}'.format(f1(unsampled_data_prediction_ADA,original_df_with_pcs['Attrition_Flag'])))
print('F1 Score of SVM Model On Original Data (Before Upsampling) - {}'.format(f1(unsampled_data_prediction_SVM,original_df_with_pcs['Attrition_Flag'])))

F1 Score of RF On Original Data - 0.6452347083926031
F1 Score of AdaBoost On Original Data - 0.553411131059246
F1 Score of SVM On Original Data - 0.5519779208831647

5结果

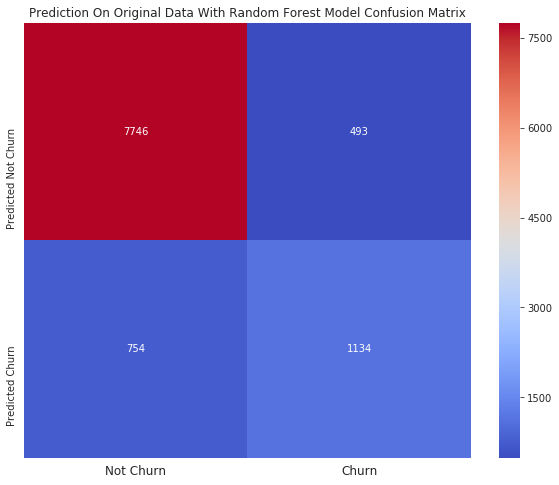
下马查看使用上面 7 个特征训练出来的随机森林模型在原始数据上的预测结果。

plt.figure(figsize=(10, 8))
ax = sns.heatmap(confusion_matrix(unsampled_data_prediction_RF,original_df_with_pcs['Attrition_Flag']),annot=True,cmap='coolwarm',fmt='d')
ax.set_title('Prediction On Original Data With Random Forest Model Confusion Matrix')
ax.set_xticklabels(['Not Churn','Churn'],fontsize=12)
ax.set_yticklabels(['Predicted Not Churn','Predicted Churn'],fontsize=10)

bottom, top = ax.get_ylim()
ax.set_ylim(bottom + 0.5, top - 0.5)

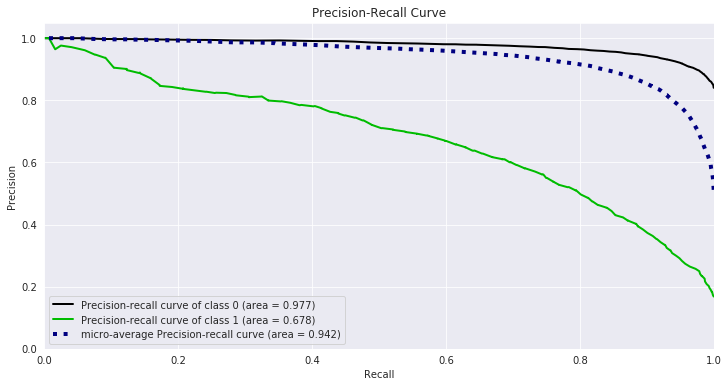
最后绘制 PR 曲线（查准-查全曲线）。

plt.figure(figsize=(16, 8))
unsampled_data_prediction_RF = rf_pipe.predict_proba(original_df_with_pcs[X_features])
skplt.metrics.plot_precision_recall(original_df_with_pcs['Attrition_Flag'], unsampled_data_prediction_RF, figsize=(12,6));