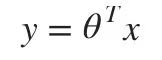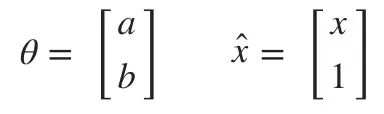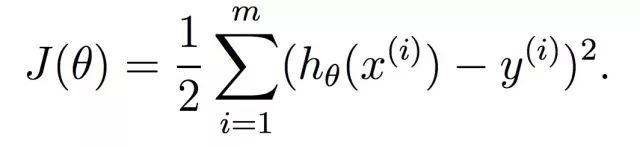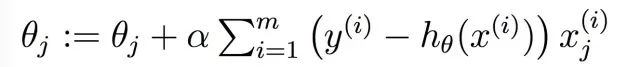干货|简单理解梯度下降及线性回归

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

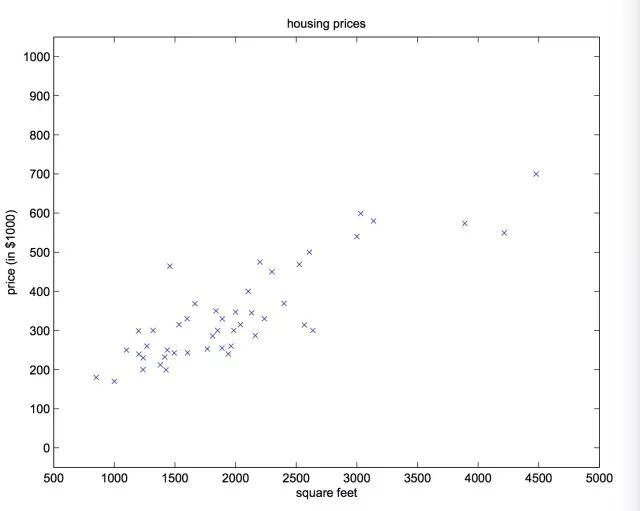
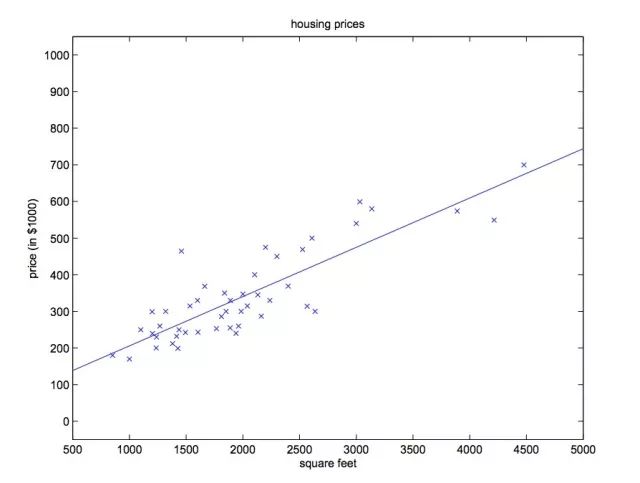
在回归分析中，一个自变量和一个因变量的关系可用一条直线近似表示，称为一元线性回归分析。当自变量大于一个的时候，称为多元线性回归。以房价-住宅面积为例。

我们希望模型拟合出一条直线 y=ax+b，以此表示住宅面积和房价之间的关系。当二维坐标系上分布的点离直线的距离之和越小（大多数点离直线很近），拟合的效果越好。此时你输入X（住宅面积），模型就会输出一个与真实值相近的预测值（房价）。更一般直线方程表示为：

用向量的内积表示方程会带来很多便利（以后会知道的）。

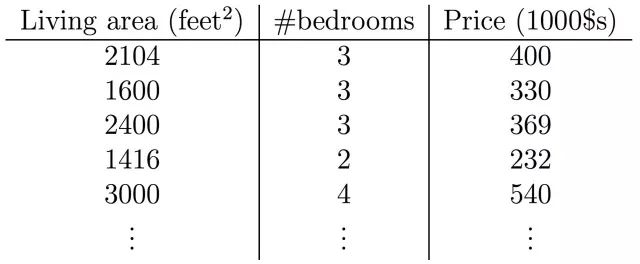
但如果房价不仅与住宅面积有关，还和卧室的数量有关。直线方程仍然可以同样的式子（向量的内积）表示。

显然，这时的点分布在一个三维空间，我们要用一个平面去拟合房价与住宅面积以及卧室之间的关系，如果三维空间上的点离平面的距离之和最小（大多数点离平面很近），我们认为此时的模型是最好的。

这样我们把在二维的线性回归推广到三维。在n维空间中，n-1个自变量与1个因变量的关系可以表示为n-1维的超平面。

上面我们将坐标系中上所有点到超平面(超过3维则无法画出图像)的距离之和作为模型好坏的判别标准。距离之和越小，则可认为模型越好。则我们的损失函数定义为：

损失函数的值 等于 对每个样本点的预测值与实际值差的平方和求和。之所以对平方和求和，是为了避免正负误差相互抵消 。（使用预测值与实际值差与使用上面的距离是等价的，而且计算量更小）1/2 是为了之后求偏导的时候可以让式子的系数等于1而存在。（1/2有没有都没关系，系数只要非0，对结果都不会有影响，因为在比较两个不同模型的优劣的时候，实际是比较他们损失函数的值，两个数值乘以同一个非0因子，他们的大小关系不会改变。）

得出损失函数之后，我们就得到了一个求解最佳模型的策略——求解使损失函数达到最小的参数𝜃。这里给大家介绍一种求解最优解的一个办法梯度下降。

学过高等数学的pong友肯定知道，顺着梯度方向，函数值增加最快，逆着梯度函数值下降越快。所以在求解一个无约束求最值的问题，梯度下降是一个非常常用的方法。（求最大和求最小是等价的，例如上面的损失函数加一个负号，学习的过程就变成一个求解损失函数取最大值时的模型参数过程）

梯度下降的过程可以概括为一个递推表达式：

更新后的参数 = 当前参数 - 学习速度*当前梯度

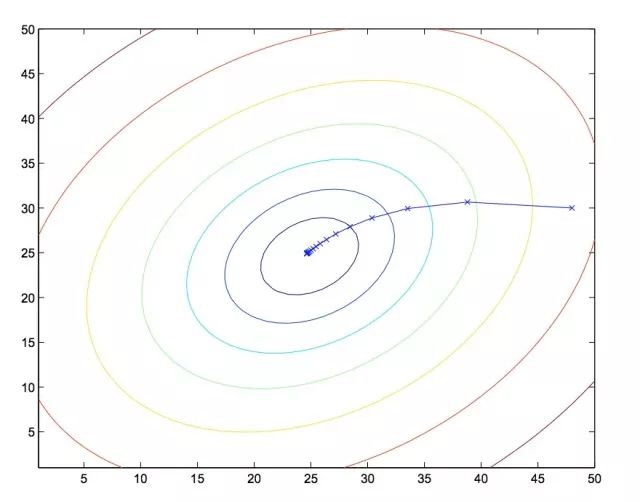
上式中，学习速度又称步长，用来控制每次迭代参数的改变量。所以梯度下降的关键在于不断计算当前的梯度，按照一定的学习速度，更新模型参数，直到收敛到极值。

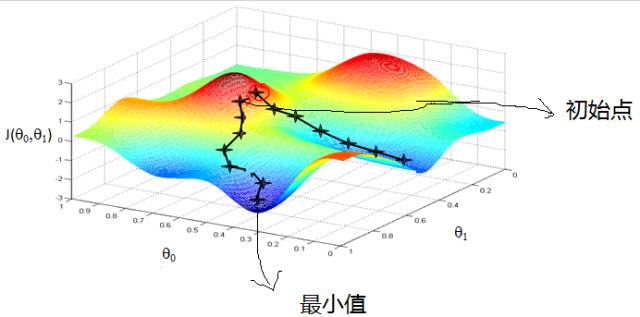
关于能否达到全局最优值。如果该函数是凸函数，则必定能收敛大最小值；否则能否达到全局最优不仅取决于初值，学习速度也会影响。如上图所示，初值选取不一样，梯度下降所指向的极小值也不一样。如果说学习速度过大，梯度下降有可能会进入到另一局部最优解中。

梯度下降算法也有很多种，最常见的有批量梯度下降算法、随机梯度下降算法，他们各有有优缺点。

批量梯度下降： 求梯度的时候利用了所有的样本

随机梯度下降：求梯度的时候随机使用一个样本

• 批量梯度可以保证每次更新参数可以使得模型被优化，因为批量梯度下降算出的梯度是正确的（使用了所有的样本）；而随机梯度下降由于每次更新只选择使用一个样本来求梯度，所求出的梯度往往没有那么准确。但是批量梯度下降每次迭代的开销很大（数据量很大时，计算梯度非常耗时间）。

• 随机梯度计算的梯度虽然不是很准确，但是它迭代的速度很快，每次接近最小值一点点，也还是能达到极值。在接近极值的时候，随机梯度会在极值附近震荡，不容易踩到极小值。所以在数据量很大，对精度要求并没特别严苛的时候使用随机梯度下降是一个不错的选择。

• 也有一个小批量梯度下降算法，每次只用少量的数据计算梯度，提高了梯度的准确率，也不需要很大迭代的开销。但是并不能说明这种方法比随机梯度和批量梯度好。

此外，在梯度下降中，要适当控制学习速度，特别是在接近最优值附近的时候，过大的学习速率会越过最优值，在最优值附近震荡。还有在开始学习的时候，如果学习速率很小，则需要更多次迭代才能达到局部最优。

回到线性回归，用批量梯度下降来求解线性回归模型的最佳参数。（用随机梯度也是可以，这里不过是举例）那么我们首先要求解梯度

上式为J(𝜃)对𝜃求偏导，1/2其实只是为了抵消求导产生的那个2的因子。更新一次的过程如下所示。

训练的过程就是不断的求偏导，更新模型参数，直到损失函数收敛，训练过程就结束了。

训练完的线性回归模型接受你的输入，然后输出一个预测值。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~