梯度下降算法综述！-技术圈

转自：狗熊会作者：亓颢博

今天要和大家分享的是梯度下降算法的综述，我们将结合2016年的一篇梯度下降算法的综述文章An overview of gradient descent optimization algorithms进行介绍并在此基础上进行一定的分析和补充。

背景介绍

梯度下降算法最经典的优化算法之一，在最优化领域占据十分重要的地位。它最早被柯西[Cauchy, 1847]首先提出，是最基础的一阶优化算法。假设我们的目标寻找光滑目标函数的极小值点，其中是模型的参数。梯度下降算法的更新公式为

其中，表示算法在第次迭代中得到的数值解，表示目标函数关于参数的一阶导数(即梯度)，超参数称为步长(step size)或学习率(learning rate)。所谓梯度下降，就是沿着目标函数的负梯度方向(当前点目标函数值下降趋势最大的方向)前进搜索极小值点，走多远由学习率参数决定，见图1。由于在极小值点处梯度为0，因此直觉上梯度下降算法最终会停在梯度为0的点，而这个点在一定假设条件下就是极小值点。由此，产生了一系列和梯度下降算法相关的理论问题，如收敛速率(convergence rate)、学习率的选取以及如何加速算法的收敛等[Curry, 1944, Nemirovski et al., 2009, Rakhlin et al., 2012, Chen et al., 2016, Toulis and Airoldi, 2017, Gitman et al., 2019]。

图1：梯度下降算法示意图

随着近年来深度学习领域的蓬勃兴起，梯度类算法成为了优化神经网络的最重要的方法。各种深度学习的框架(如Caffe, Keras, TensorFlow and PyTorch)中，均支持各种各样的梯度类优化器。梯度类方法在深度学习中如此重要的主要原因是深度神经网络中数以百万、千万级别的待优化参数使得诸如牛顿法和拟牛顿法等高阶优化方法不再可行，而梯度类方法借助GPU计算资源的支持可以进行高效的运算。然而天下没有免费的午餐，当我们使用一阶优化算法获取其计算可行性上的好处时，付出的代价便是一阶算法较慢的收敛速率。尤其是当目标函数接近病态系统时，梯度类算法的收敛速度会变得更加缓慢。除此之外，由于深度神经网络的损失函数极其复杂且非凸，梯度类算法优化得到的模型参数的性质未知，依赖于算法的参数选取和初值的选取。因此，目前深度学习中的梯度类算法实际上是某种意义上的黑箱算法，其可解释性仍然面临着巨大挑战。

梯度下降算法的变体

在第一部分的背景介绍中，我们将称为目标函数，这里的是一个确定的函数形式，例如. 在实际的机器学习问题中，我们往往考虑随机优化问题。具体来说，假设服从某一分布，给定损失,其中是我们感兴趣的参数。参数的真值满足如下的等式:

由于分布是未知的，上述优化问题无法直接被计算。假设我们获取了一组观测样本(往往假设独立同分布)，那么我们转而考虑风险极小化问题：

此时通常被称为损失函数，例如平方损失、交叉熵损失等等。本身是的一个估计量，而我们的通过算法寻找的其实是。相比较于确定性目标函数，这里的损失函数引入了一个新的超参数，即样本量。而计算梯度时使用的样本量不同，带来了不同的梯度下降算法。

批量梯度下降

批量梯度下降(Batch gradient descent, BGD)，某些文献中也称为(Full gradient, FG)，其本质就是使用全样本数据计算梯度。假设参数，全样本为，则BGD算法单次迭代的复杂度约为。BGD算法的优缺点十分鲜明。其主要优点在于理论性质良好，保证能够找到极小值点。如果损失函数是凸(强凸)函数，BGD算法能以次线性(线性)的收敛速率找到全局极小值点。缺点则是，当样本量很大时计算效率很低。例如计算机视觉中的ImageNet[Deng et al., 2009] 数据集，训练样本量超过一百万，即使忽略的影响也是非常巨大的计算成本。此外，BGD算法由于要使用全样本数据，也不适用于在线学习(Online learning)的情形。

随机梯度下降

随机梯度下降(Stochastic gradient descent, SGD)与BGD不同，SGD每次更新时仅仅是用一个样本来计算梯度，因此SGD算法单次迭代的复杂度约为，与BGD相比计算效率大大提升，而且SGD适用于在线学习的情形，来一个样本就可以通过SGD更新一次。SGD付出的代价在于它在梯度中引入了额外的方差。尽管在给定全样本的条件下，单个样本计算的梯度是全样本的无偏估计，但是单个样本梯度方向很难和全样本方向一致，因此SGD的更新是极其波动的。在常数学习率下，SGD算法即使在损失函数为凸(强凸)函数的条件下也不能准确找到极小值点，最终的解和极小值点之间的距离受到学习率和梯度方差上界的影响。

小批量梯度下降

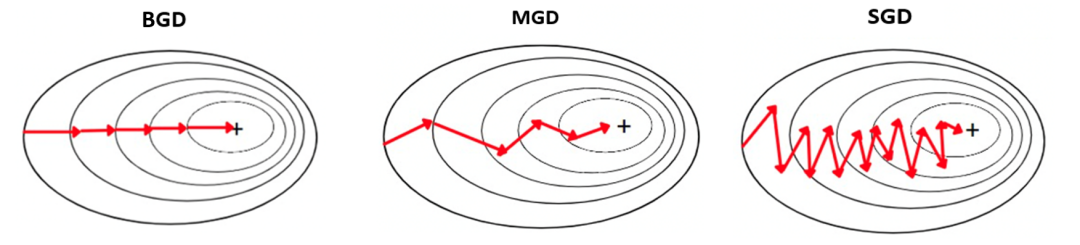小批量梯度下降(Mini-batch gradient descent, MGD)可以看做是BGD和SGD的一种折中的选择，它也是目前在深度学习中实际上使用最为广泛的梯度下降算法，许多文章中所指的SGD实际上为MGD算法。每次更新时使用样本量为batch size, 的样本来计算梯度，因此MGD算法单次迭代的复杂度约为，与BGD相比计算效率有所提升，同时引入的梯度噪声方差小于SGD，稳定性更好。当然MGD算法也有自己的问题，它引入了新的超参数。在实际深度学习任务中，学者发现的选取不仅影响算法的收敛效率，同样影响最终的外样本精度。一般而言的取值范围在之间。最后，我们给出三种使用不同样本量的梯度下降算法的对比示意图。

图2：三种梯度下降算法的对比示意图

梯度下降算法的改进算法

如前所说，梯度下降算法作为一阶算法有其固有的局限性，仅仅使用损失函数的一阶信息进行更新是比较“短视”的做法，在病态系统下收敛速度极为缓慢。学者们也提出了一系列方法来加速梯度下降算法，主要的思路是对梯度下降法的两个主要组成部分进行修改，即更新方向和学习率。我们接下来主要介绍其中几种十分重要的算法。请注意，以下算法原始版本均是在非随机优化或BGD的条件下讨论的，但是在实际深度学习的应用中往往是使用了MGD的版本，我们在下文的介绍中并不区分这些细节。

动量梯度下降

动量梯度下降(Gradient Descent with Momentum)法 [Polyak, 1964, Ning, 1999]，也被称为重球(Heavy Ball, HB)方法，是对梯度下降算法的经典改进算法，其更新公式如下：

其中被称为动量参数，文献中的推荐值为0.9。它的核心思想是对梯度下降的更新方向进行调整，考虑使用历史梯度信息的指数加权平均作为参数更新的方向。动量梯度下降算法主要带来了两个方面的改进：(1) 加速梯度下降算法。动量一词源于物理学，我们可以很形象的理解为物体沿山坡下滑的过程中的任意时刻的速度可以分解为当前位置的坡度下降的方向(当前梯度方向)和物体的惯性(历史速度方向)的矢量和。因此当我们考虑历史梯度信息后，梯度下降算法会下降得更快；(2) 抑制震荡。梯度下降算法会受到损失函数海森矩阵的条件数(海森矩阵的最大特征根与最小特征根的比值)的影响 [Sutton, 1986]，条件数越大海森矩阵的病态程度越高，此时梯度方向对参数空间的某些方向极度敏感，我们能够观察到参数的更新路径震荡剧烈。动量梯度下降法能够累计在正确前进方向的梯度，并且抵消部分敏感方向的震荡幅度。在理论研究方面，可以证明动量梯度下降法主要是修正了海森矩阵条件数的影响，即将最优收缩系数中的变为了，从而加速收敛。

Nesterov动量梯度

Nesterov动量梯度(Nesterov accelerated gradient, NAG)方法 [Nesterov, 1983]，是动量梯度下降法的改进版本，其更新公式如下：

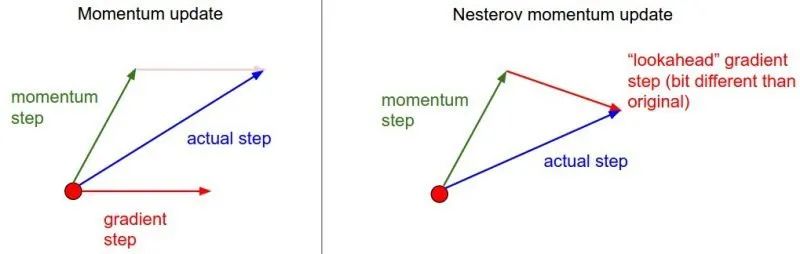其中动量参数的推荐值仍为0.9。NAG考虑的是一个更加“聪明”的小球，它并不是短视地考虑当前时刻的梯度，而是超前考虑未来时刻的梯度，即按照动量方向前进至处的梯度。当梯度方向发生变化时，动量梯度的纠正机制往往需要累积几步，而NAG能够更早的进行纠正。这种超前的思路使得NAG能够进一步抑制震荡，从而加速收敛。当损失函数为凸函数时，可以证明NAG算法的收敛速率由提升为。

图3：动量梯度下降与NAG的对比示意图

AdaGrad

AdaGrad[Duchi et al., 2011]从学习率的角度考虑加速梯度下降算法，传统的梯度下降算法之所以受制于病态系统的影响，归根结底是因为所有的参数共享了相同的学习率。为保证算法收敛，学习率受制于海森矩阵特征值较大的参数方向而变得很小，导致其他方向更新步长过小优化缓慢。如果我们能够给每个参数赋予不同的学习率，那么就有可能极大地加速梯度下降算法的收敛。同时，AdaGrad能够在迭代过程中自动调整参数的学习率，这被称为自适应学习率(Adaptive learning rate)方法。其更新公式如下：

这里表示对应元素相乘，根号也是作用在向量的每一个元素上，是为了保证除法的数值稳定性添加的小量。可以看到AdaGrad记录了历史梯度的逐元素累积平方和，并使用该累积和的平方根的逆作为学习率权重。AdaGrad的主要贡献在于可以进行学习率的自适应调整，同时对梯度下降法略有加速。但是它也有很明显的缺点，更新公式的分母是所有历史信息的求和，因此会随着迭代变得越来越大，从而使得学习率衰减过快。AdaGrad算法在实际操作中往往会出现算法找到极小值点之前提前停止的情况。

AdaDelta

AdaDelta[Zeiler, 2012]是AdaGrad的延伸和改进版本，它主要是为了解决Adagrad中历史梯度累积平方和单调递增的问题。AdaDelta不再使用全部历史信息，而是提出使用某个固定窗宽内的历史梯度信息计算累计平方和。由于计算固定窗宽内的梯度累积平方和需要存储个历史梯度平方的信息，AdaDelta转而使用指数加权的方式累积历史信息：

其中指数加权参数的推荐值为0.9。进而有迭代公式：

作者在文章中指出，之前的梯度类算法(包括原始梯度下降、动量梯度下降和AdaGrad)更新公式中参数的单位并没有一致。这里具体是指，和各自有自己的单位和尺度，在之前的算法里并没有考虑这个问题。作者考虑修正这个问题，因此AdaDelta最终的更新公式变为：

可以看到，分子使用保证了单位的一致性，同时代替了学习率的作用。因此，AdaDelta算法不再需要设定学习率。

RMSprop

RMSprop[Tieleman and Hinton, 2012]和AdaDelta的思路十分相似，两个算法同年分别被Hinton和Zeiler提出，有趣的是Hinton正是Zeiler的导师。RMSprop最早出现在Hinton在Coursera的课程中，这一算法成果并未发表。其更新公式与第一阶段的AdaDelta一致：

其中指数加权参数的推荐值为0.9，学习率的推荐值为0.001。

Adam

自适应矩估计算法(Adaptive Moment Estimation, Adam)[Kingma and Ba, 2015]是将搜索方向和学习率结合在一起考虑的改进算法，其原论文引用量为ICLR官方引用最高的文章。Adam的思路非常清晰：搜索方向上，借鉴动量梯度下降法使用梯度的指数加权；学习率上，借鉴RMSprop使用自适应学习率调整。所谓矩估计，则是修正采用指数加权带来的偏差。其更新公式具体如下：

作者推荐参数的取值为，以及小量。在实际应用中，Adam的收敛速度通常优于其他梯度类优化算法，这也是Adam十分受欢迎的一大原因。相比于之前的算法，Adam需要记录两个历史信息和，这使得Adam和AdaDelta一样，需要多储存一个长度为的向量。

AdaMax 与 Nadam

我们在这一小节简要介绍一下Adam的两个重要变体：AdaMax与Nadam。AdaMax是Adam作者在原论文后面自行提出的拓展。其主要思路就是保持搜索方向保持不变，调整自适应学习率的权重，从逐元素2范数推广到逐元素范数，甚至是无穷范数：

对于无穷范数的情形，作者建议不再对进行纠偏。

Nadam[Dozat, 2016]则是将Adam中关于搜索方向的部分改为使用Nesterov动量。在引入其更新公式之前，我们首先给出NAG的等价更新形式。

可以看到，NAG得到等价形式与动量梯度下降法的区别仅仅在最后一步，动量梯度下降法参数的更新量为，而NAG中则是。回顾Adam的更新公式(忽略的部分)：

仿照NAG的等价形式，我们将上述等式中的替换为即可得到Nadam的更新公式：

一些可视化结果

我们展示两幅图片来对比不同的优化算法的表现，如图4所示。

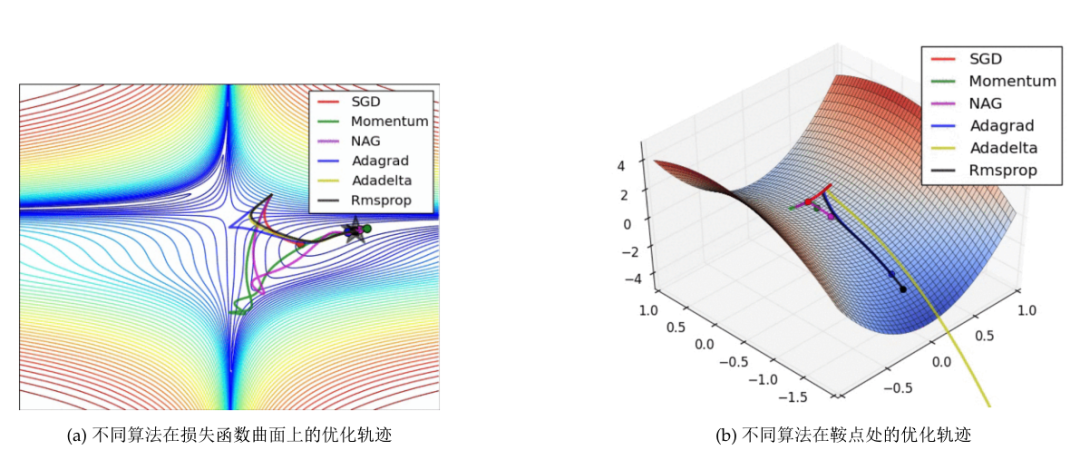图4：梯度下降算法的可视化结果

图4-(a)展示的是六种梯度下降改进算法在Beale函数的函数曲面的优化路径。等高线由红变蓝的过程表示函数值由大到小，最小值点在图中由五角星标出。所有的算法均从同一点出发，可以看到自适应学习率类的算法(AdaGrad, AdaDelta和RMSprop)的优化路径直接走向了右边的极小值点，但是动量梯度法(绿色曲线)和NAG(紫色曲线)均是先走到了另一处狭长的区域，再转向极小值点，且NAG的纠正速度快于动量梯度法。

图4-(b)展示的是六种梯度下降改进算法在鞍点附近的优化路径。所谓鞍点就是，满足一阶条件等于0但是海森矩阵的特征值有正有负的点。由于梯度下降算法仅仅考虑一阶条件，理论上会受到鞍点的困扰。可以看到，SGD(红色曲线)在鞍点处停止，动量梯度法(绿色曲线)和NAG(紫色曲线)在鞍点处停留一会后逐渐脱离鞍点，而三种自适应学习率算法则能够快速摆脱鞍点。

梯度类算法相关研究

并行SGD和分布式SGD

在当今无处不在的大数据时代，数据的分布方式和使用方式都不再像原来一样单一。与之对应的，当数据仍然保存在本地，学者们开始研究如何在单机上实现并行SGD[Niu et al., 2011]来进行加速；当数据分散地保存在不同的节点，如何实现分布式SGD[Jeffrey Dean and Ng., 2012, Mcmahan and Streeter, 2014, Sixin Zhang and LeCun, 2015]；更进一步地，对于数据节点十分庞大而又需要保护用户隐私的时代，联邦学习(Federated Learning)版本的SGD[H. Brendan McMahan and y Arcas, 2016]同样也是学者们关注的问题。由于篇幅原因，我们不在这里进行展开。

梯度类算法的训练策略

除了算法层面的改进，与算法相配套的训练策略或者其他技术同样对训练模型有很大的影响。例如：

数据打乱和课程式学习. 有学者指出避免让数据以固定单一的方式进入模型训练能够提升模型的泛化能力，因此在深度学习模型的训练中人们在每一次遍历全样本后都会进行数据打乱(Shuffling)。另一方面，有学者指出让数据以某种有意义的顺序参与模型训练能够使模型更快收敛且表现不错，这样的方法被称为课程式学习(Curriculum Learning)[Yoshua Bengio and Weston, 2009].
批量归一化. 批量归一化(Batch normalization)[Ioffe and Szegedy, 2015]是卷积神经网络中经常使用的技术，它能够对每个小批量的数据在模型的某些节点进行归一化。大量实验表明，这种技术能够加速梯度类算法的收敛、让梯度类算法使用更大的初始学习率以及减少参数初始化的影响。
早停. 通过监控验证集的精度指标来决定是否要提前终止算法训练。
梯度噪声. [Neelakantan et al., 2015]提出在梯度上增加独立的高斯噪声，来帮助梯度类算法增加稳健性。他们猜测，增加的梯度噪声能够帮助算法跳过局部鞍点和次优的极小值点。

梯度类算法仍然面临的挑战

尽管我们已经介绍了非常多的梯度类算法的改进算法，但是梯度类算法仍然面临着许多挑战。

选择合适的学习率是非常困难的事情。尽管在传统的优化领域和我们之前提到的自适应学习率算法提供了很多解决这个问题的方法。在深度模型的训练中，这些已有的方法仍然会遇到问题，因此这仍是一个需要小心考虑和诸多尝试的问题。
尽管梯度下降算法在理论上有许多性质和结论，但实际得到神经网络往往不满足已有结论的前提假设。在我们优化超高维非凸的损失函数时，如何保证算法不被鞍点 [Zeiler, 2014]、平坦区域所困扰，依然是十分挑战的问题。
对于超高维得到损失函数，梯度类算法表现地像黑箱优化器，目前上没有特别好的方法对这种超高维优化进行可视化分析。

参考文献

Augustin-Louis Cauchy. Mode grale pour la rlution des systs d’ations simultan. Comptes rendus des sces de l’ Acade des sciences de Paris, pages 536–538, 10 1847.

Xi Chen, Jason D Lee, Xin T Tong, and Yichen Zhang. Statistical inference for model parameters in stochastic gradient descent. arXiv preprint arXiv:1610.08637, 2016.

Haskell B. Curry. The method of steepest descent for non-linear minimization problems. Quarterly of Applied Mathematics, pages 258–261, 2 1944.

Jia Deng, Wei Dong, Richard Socher, Li Jia Li, and Fei Fei Li. Imagenet: A large-scale hierarchical image database. In IEEE Conference on Computer Vision and Pattern Recognition, 2009.

Timothy Dozat. Incorporating nesterov momentum into adam. ICLR Workshop, 2016.

John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(7):257–269, 2011.

Igor Gitman, Hunter Lang, Pengchuan Zhang, and Lin Xiao. Understanding the role of momentum in stochastic gradient methods. In Proceedings of 33rd Conference and Workshop on Neural Information Processing Systems, 2019.

Daniel Ramage Seth Hampson H. Brendan McMahan, Eider Moore and Blaise Aguera y Arcas. Communication-efficient learning of deep networks from decentralized data. In International Conference on Machine Learning (ICML), 2016.

Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd annual international conference on machine learning, 2015.

Rajat Monga Kai Chen Matthieu Devin Quoc V. Le Mark Z. Mao Marc Aurelio Ranzato Andrew Senior Paul Tucker Ke Yang Jeffrey Dean, Greg S. Corrado and Andrew Y. Ng. Large scale distributed deep networks. In Neural Information Processing Systems Conference (NIPS 2012), pages 1–11, 2012.

Diederik P. Kingma and Jimmy Lei Ba. Adam: A method for stochastic optimization. In International Conference on Learning Representations, pages 1–13, 2015.

H. Brendan Mcmahan and Matthew Streeter. Delay-tolerant algorithms for asynchronous distributed online learning. In Neural Information Processing Systems Conference (NIPS 2014), pages 1–9, 2014.

A. Neelakantan, L. Vilnis, Q. V. Le, I. Sutskever, and J. Martens. Adding gradient noise improves learning for very deep networks. arXiv preprint arXiv:1511.06807., 2015.

Arkadii S. Nemirovski, Anatoli Juditsky, Guanghui Lan, Shapiro, and A. Robust stochastic approximation approach to stochastic programming. SIAM Journal on Optimization, 19(4):1574–1609, 2009.

Y. E. Nesterov. A method for solving the convex programming problem with convergence rate o(1/ ). Dok- l.akad.nauk Sssr, 269, 1983.

Q. Ning. On the momentum term in gradient descent learning algorithms. Neural Netw, 12(1):145–151, 1999.

F. Niu, B. Recht, C. Re, and S. J. Wright. Hogwild!: A lock-free approach to parallelizing stochastic gradient descent. In Neural Information Processing Systems Conference (NIPS 2011), pages 1–22, 2011.

B. T. Polyak. Some methods of speeding up the convergence of iteration methods. Ussr Computational Mathe- matics Mathematical Physics, 4(5):1–17, 1964.

A. Rakhlin, O. Shamir, and K. Sridharan. Making gradient descent optimal for strongly convex stochastic optimization. In International Conference on Machine Learning, 2012.

Anna Choromanska Sixin Zhang and Yann LeCun. Deep learning with elastic averaging sgd. In Neural Information Processing Systems Conference (NIPS 2015), pages 1–9, 2015.

R.S. Sutton. Twoproblemswith backpropagationand other steepest-descent learning proceduresfor networks. proc cognitive sci soc, 1986.

T. Tieleman and G. Hinton. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning, pages 26–31, 2012.

Panos Toulis and Edoardo M. Airoldi. Asymptotic and finite-sample properties of estimators based on stochastic gradients. Eprint Arxiv, 45(4):1694–1727, 2017.

Ronan Collobert Yoshua Bengio, Jme Louradour and Jason Weston. Curriculum learning. In Proceedings of the 26th annual international conference on machine learning, pages 41–48, 2009.

Matthew D. Zeiler. Adadelta: An adaptive learning rate method. arXiv preprint arXiv:1212.5701, 2012.

Matthew D. Zeiler. Identifying and attacking the saddle point problem in high-dimensional nonconvex optimization. arXiv preprint arXiv:1406.2572, 2014.

- END -