【深度学习】PyTorch 中的线性回归和梯度下降
我们正在使用 Jupyter notebook 来运行我们的代码。我们建议在Google Colaboratory上遵循本教程。你可以查看此链接以获取有关其用法的更多信息。
https://www.analyticsvidhya.com/blog/2020/03/google-colab-machine-learning-deep-learning/
为了完成本教程,假设你已具备 PyTorch 和 Python 编程的先验知识。不需要机器学习的先决知识。你可以查看我们之前关于 PyTorch 的博客以熟悉它。
https://www.analyticsvidhya.com/blog/2021/04/a-gentle-introduction-to-pytorch-library/
线性回归简介
反向传播是深度学习中一种强大的技术,用于更新权重和偏差,从而使模型能够学习。为了更好地说明反向传播,让我们看一下线性回归模型在 PyTorch 中的实现
线性回归是机器学习中的基本算法之一。线性回归在输入特征 (X) 和输出标签 (y) 之间建立线性关系。
在线性回归中,每个输出标签都表示为使用权重和偏差的输入特征的线性函数。这些权重和偏差是随机初始化的模型参数,然后通过数据集的每个训练/学习周期进行更新。在经过一次训练数据迭代后训练模型和更新参数被称为一个时期。
所以现在我们应该训练模型几个时期,以便权重和偏差可以学习输入特征和输出标签之间的线性关系。
因此,在本教程中,让我们创建一个假设数据模型,该模型由芒果和橙子的作物产量组成,并给出了特定地点的平均温度、年降雨量和湿度。训练数据如下:
| 地区 | 温度(华氏度) | 降雨量(毫米) | 湿度 (%) | 芒果(吨) | 橙子(吨) |
|---|---|---|---|---|---|
| A | 73 | 67 | 43 | 56 | 70 |
| B | 91 | 88 | 64 | 81 | 101 |
| C | 87 | 134 | 58 | 119 | 133 |
| D | 102 | 43 | 37 | 22 | 37 |
| E | 69 | 96 | 70 | 103 | 119 |
| F | 74 | 66 | 43 | 57 | 69 |
| G | 91 | 87 | 65 | 80 | 102 |
| H | 88 | 134 | 59 | 118 | 132 |
| I | 101 | 44 | 37 | 21 | 38 |
| J | 68 | 96 | 71 | 104 | 118 |
| 钾 | 73 | 66 | 44 | 57 | 69 |
| 升 | 92 | 87 | 64 | 82 | 100 |
| 米 | 87 | 135 | 57 | 118 | 134 |
| N | 103 | 43 | 36 | 20 | 38 |
| 哦 | 68 | 97 | 70 | 102 | 120 |
在线性回归中,每个目标标签都表示为输入变量的加权总和以及偏差,即
芒果 = w11 * 温度 + w 12 * 降雨量 + w 13 * 湿度 + b 1
橙子 = w 21 * 温度 + w 22 * 降雨量 + w 23 * 湿度 + b 2
最初,权重和偏差是随机初始化的,然后在训练过程中进行相应的更新,以便这些权重和偏差能够预测任何地区的芒果和橙子产量,前提是温度、降雨量和湿度达到一定的准确度。
简而言之,这就是机器学习。
所以现在让我们开始使用 Pytorch 实现
进口
导入所需的库
import torch
import numpy as np
加载数据
上表中给出的训练数据可以使用 NumPy 表示为矩阵。所以让我们分别定义输入和目标,
inputs = np.array([[73, 67, 43],
[91, 88, 64],
[87, 134, 58],
[102, 43, 37],
[69, 96, 70],
[74, 66, 43],
[91, 87, 65],
[88, 134, 59],
[101, 44, 37],
[68, 96, 71],
[73, 66, 44],
[92, 87, 64],
[87, 135, 57],
[103, 43, 36],
[68, 97, 70]],
dtype='float32')
targets = np.array([[56, 70],
[81, 101],
[119, 133],
[22, 37],
[103, 119],
[57, 69],
[80, 102],
[118, 132],
[21, 38],
[104, 118],
[57, 69],
[82, 100],
[118, 134],
[20, 38],
[102, 120]],
dtype='float32')
输入矩阵和目标矩阵都作为 NumPy 数组加载。
这应该使用torch.from_numpy()方法转换为torch张量 ,
inputs = torch.from_numpy(inputs)
targets = torch.from_numpy(targets)
我们可以检查两个张量,
print(inputs)
输出:
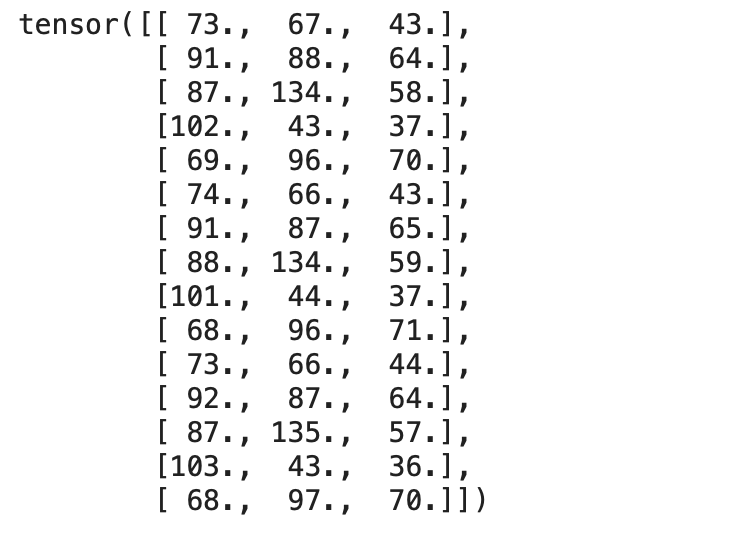
print(targets)
输出:
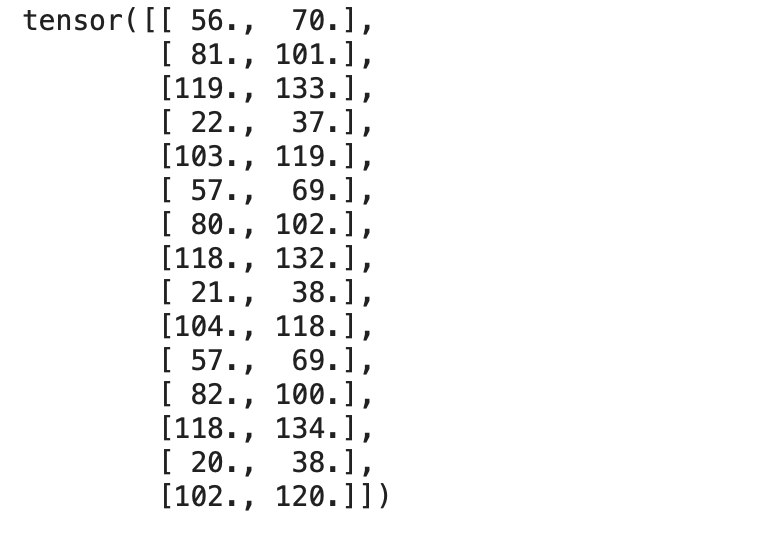
现在让我们创建一个TensorDataset,它将输入和目标张量包装到一个数据集中。让我们从torch.utils.data导入TensorDataset方法。
我们可以以元组的形式访问数据集中的行。
from torch.utils.data import TensorDataset
dataset = TensorDataset(inputs, targets)
我们可以使用 Python 中的索引从定义的数据集中访问输入行和相应的目标。
dataset[:3]

现在让我们将数据集转换为数据加载器,它可以在训练期间将数据拆分为预定义批量大小的批次。
使用 Pytorch 的DataLoader类,我们可以将数据集转换为预定义批量大小的批次,并通过从数据集中随机挑选样本来创建批次。
from torch.utils.data import DataLoader
batch_size = 3
train_loader = DataLoader(dataset, batch_size=batch_size, shuffle=True)
我们可以使用 for 循环将DataLoader 中的数据作为包含输入和相应目标的元组对访问,这使我们能够将批次直接加载到训练循环中。
# A Batch Sample
for inp,target in train_loader:
print(inp)
print(target)
break
输出:

现在我们的数据已准备好进行训练,让我们定义线性回归算法。
线性回归——从头开始
在统计建模中,回归分析是一组统计过程,用于估计因变量与一个或多个自变量之间的关系。-维基百科
让我们从头开始实现一个线性回归模型。我们应该找到上述方程中指定的最佳权重和偏差,以便它定义输入和输出之间的理想线性关系。
因此,我们定义了一组权重,如上述等式,以建立与输入特征和目标的线性关系。在这里,我们还将超参数(即权重和偏差)的requires_grad属性设置 为True。
w = torch.randn(2, 3, requires_grad=True)
b = torch.randn(2, requires_grad=True)
print(w)
print(b)
输出:

torch.randn从均值 0 和标准差 1 的均匀分布中随机生成张量。
线性回归方程为 y = w * X + b,其中
y是输出或因变量
X是输入或自变量
w & b分别是权重和偏差
因此,现在让我们定义我们的线性回归模型,
def model(X):
return X @ w.t() + b
该模型只是一个建立权重和输出之间线性关系的数学方程。
使用输入批次和权重的转置执行矩阵乘法(@ 表示矩阵乘法)。
现在让我们为一批数据预测模型的输出,
for x,y in train_loader:
preds = model(x)
print("Prediction is :n",preds)
print("nActual targets is :n",y)
break
输出:
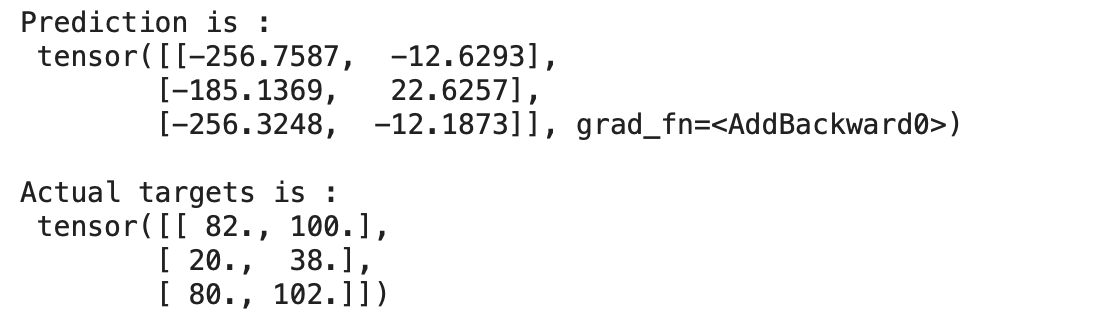
我们可以在上面看到我们的模型预测的值与实际目标相差很大,因为我们的模型是用随机权重和偏差初始化的。
显然,我们不能指望我们随机初始化的模型表现良好。
损失函数
损失函数是衡量模型表现如何的指标。损失函数在更新超参数方面起着重要作用,因此产生的损失会更少。
回归最广泛使用的损失函数之一是均方误差或L2 损失。
MSE 定义了实际值和预测值之间差异的平方平均值。MSE如下:
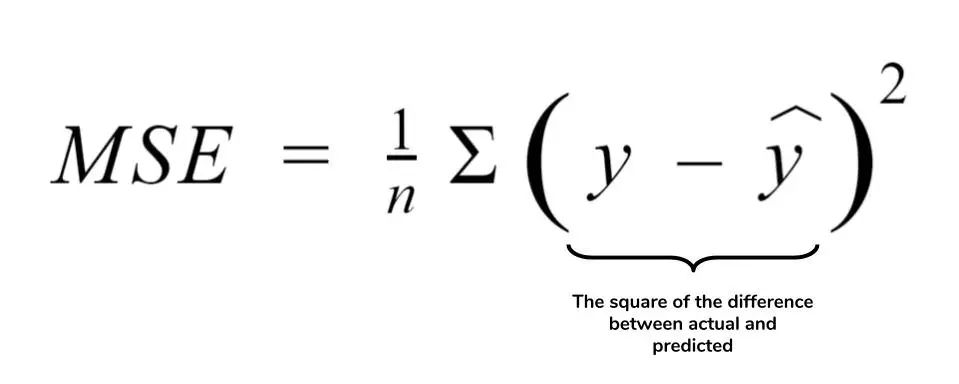
def mse_loss(predictions, targets):
difference = predictions - targets
return torch.sum(difference * difference)/ difference.numel()
.numel()方法返回张量中的元素数。
现在让我们进行预测并计算未经训练的模型的损失,
for x,y in train_loader:
preds = model(x)
print("Prediction is :n",preds)
print("nActual targets is :n",y)
print("nLoss is: ",mse_loss(preds, y))
break
输出:
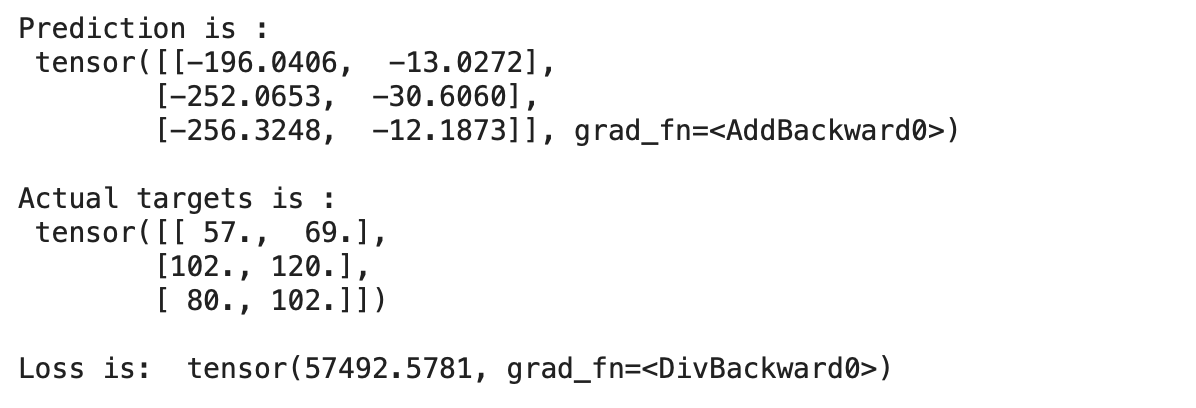
我们可以看到我们的预测与实际目标相差很大,这表明模型的损失很大。
因此,我们应该更新权重和偏差,以减少损失。这可以通过使用称为梯度下降的优化算法来完成。
梯度下降
梯度下降是一种一阶迭代优化算法,用于寻找可微函数的局部最小值。这个想法是在当前点的函数梯度(或近似梯度)的相反方向上重复步骤,因为这是最陡下降的方向。– 维基百科
梯度下降是一种优化算法,它计算损失函数的导数/梯度以更新权重并相应地减少损失或找到损失函数的最小值。
在 PyTorch 中实现梯度下降的步骤,
首先,计算损失函数
求关于自变量的损失梯度
更新权重和 bais
重复以上步骤
现在让我们开始编码并实现 50 个 时期的梯度下降,
epochs = 50
for i in range(epochs):
# Iterate through training dataloader
for x,y in train_loader:
# Generate Prediction
preds = model(x)
# Get the loss and perform backpropagation
loss = mse_loss(preds, y)
loss.backward()
# Let's update the weights
with torch.no_grad():
w -= w.grad *1e-6
b -= b.grad * 1e-6
# Set the gradients to zero
w.grad.zero_()
b.grad.zero_()
print(f"Epoch {i}/{epochs}: Loss: {loss}")
输出:
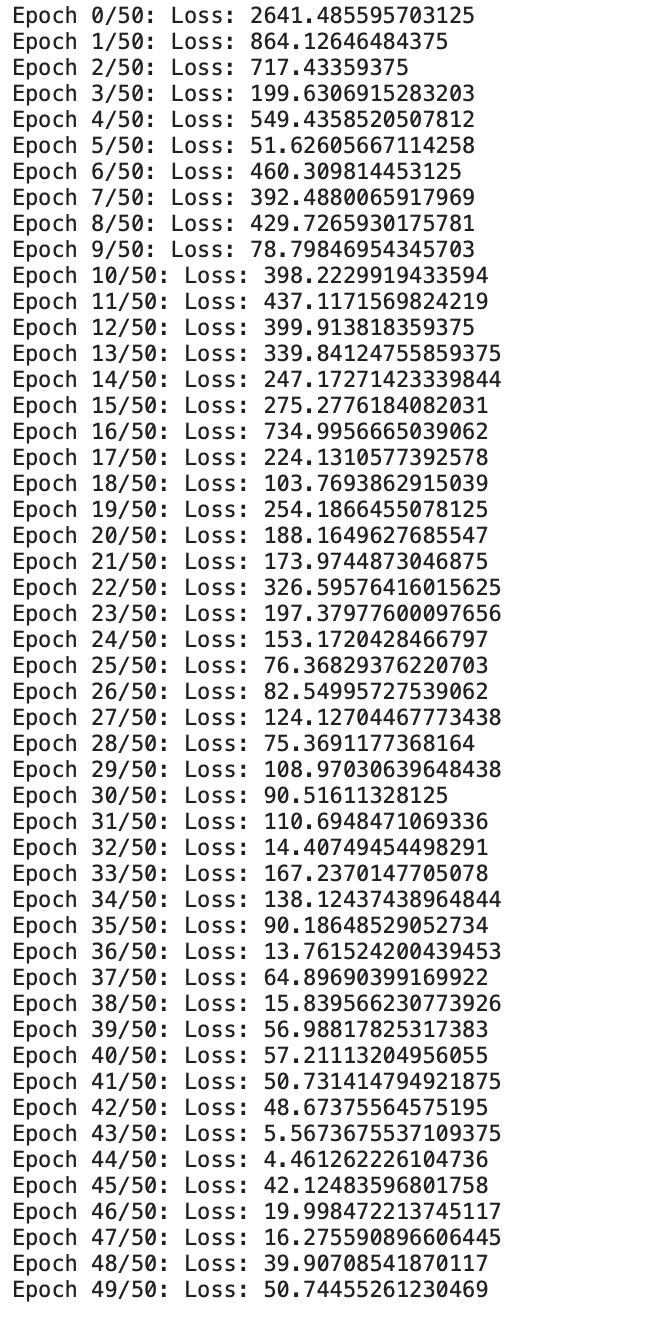
现在我们可以看到我们从头开始定制的线性回归模型正在训练给定的数据。
我们可以看到损失一直在逐渐减少。现在让我们检查一下输出,
for x,y in train_loader:
preds = model(x)
print("Prediction is :n",preds)
print("nActual targets is :n",y)
break
输出:
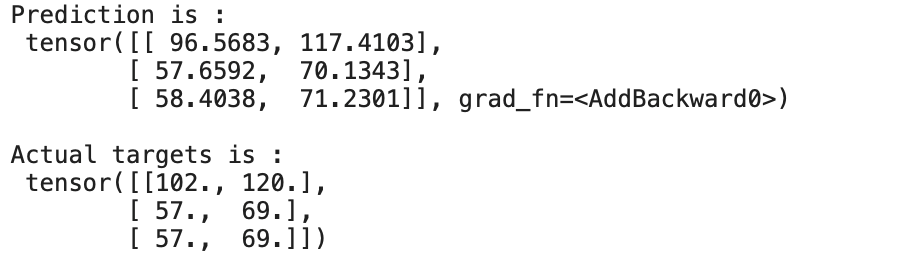
我们可以看到预测几乎接近实际目标。我们能够通过训练/更新线性回归模型的权重和偏差来预测 50 个时期。
结论
这种在数据集每次迭代后通过我们基于损失的模型使用梯度下降更新权重/参数的过程定义了深度学习的基础,它可以解决包括视觉、图像、文本等在内的大量任务
往期精彩回顾
适合初学者入门人工智能的路线及资料下载 (图文+视频)机器学习入门系列下载 中国大学慕课《机器学习》(黄海广主讲) 机器学习及深度学习笔记等资料打印 《统计学习方法》的代码复现专辑 AI基础下载 机器学习交流qq群955171419,加入微信群请扫码:
