从零开始深度学习Pytorch笔记(7)—— 使用Pytorch实现线性回归

前文传送门:
从零开始深度学习Pytorch笔记(1)——安装Pytorch
从零开始深度学习Pytorch笔记(2)——张量的创建(上)
从零开始深度学习Pytorch笔记(3)——张量的创建(下)
从零开始深度学习Pytorch笔记(4)——张量的拼接与切分
从零开始深度学习Pytorch笔记(5)——张量的索引与变换
在该系列的上一篇,我们介绍了Pytorch中的张量的数学运算,本文教会大家使用Pytorch搭建一个线性回归模型。
说到线性回归,从某种程度上可以算是最简单的机器学习模型了。具体的理论推导我这里就不多说了,网上随手一搜就有。
我们着重讲讲使用Pytorch搭建模型的过程。
首先贴出可实现的代码:
import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)#随机数种子
lr = 0.1 #学习率
#创建训练数据
x = torch.rand(20,1)*10 #shape(20,1)
y = 2*x + (5 + torch.randn(20,1)) #shape(20,1)
#构建线性回归参数
w = torch.randn((1),requires_grad=True)#随机初始化w,要用到自动梯度求导
b = torch.zeros((1),requires_grad=True)#使用0初始化b,要用到自动梯度求导
for iteration in range(1000):
#前向传播
wx = torch.mul(w,x) # w*x
y_pred = torch.add(wx,b) # y = w*x + b
#计算 MSE loss
loss = (0.5*(y-y_pred)**2).mean()
#反向传播
loss.backward()
#更新参数
b.data.sub_(lr*b.grad) # b = b - lr*b.grad
w.data.sub_(lr*w.grad) # w = w - lr*w.grad
#绘图
if iteration % 20 == 0:
plt.scatter(x.data.numpy(),y.data.numpy())
plt.plot(x.data.numpy(),y_pred.data.numpy(),'r-',lw=5)
plt.text(2,20,'Loss=%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'red'})
plt.xlim(1.5,10)
plt.ylim(8,28)
plt.title("Iteration:{}\nw:{},b:{}".format(iteration,w.data.numpy(),b.data.numpy()))
plt.pause(0.5)
if loss.data.numpy() < 1:#停止条件
break
我们来分步骤讲讲上面的代码具体的内容。
首先导入相关的库,设定学习率和随机数种子,然后创建随机数作为使用的数据。
初始化参数 w、b,由于之后需要在模型训练中不断调整 w、b 的参数值,并且会用到相关求导,所以设置 requires_grad=True,代表需要用到该张量的求导。
之后写了一个循环,每次循环先进行前向传播,计算 y 的预测值,计算 loss 损失值,然后反向传播损失,去更新参数 w、b。
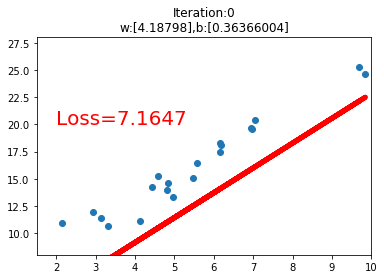
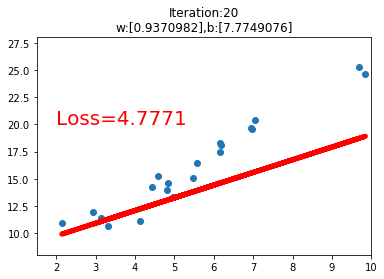
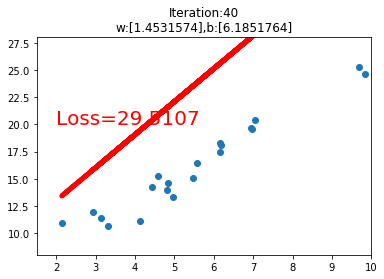
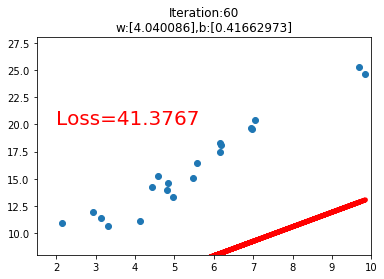
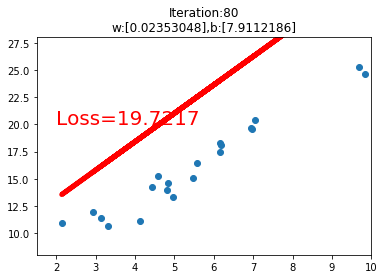
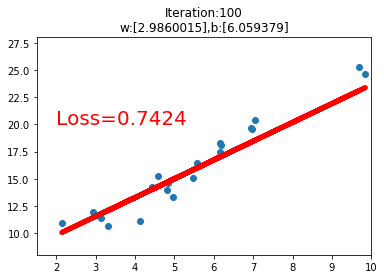
之后是一个绘图操作,绘制数据的散点图和在训练过程中的线性回归直线。
运行代码后,我们可以看到如下的几个训练过程中的可视化图,当loss损失值小于1时,停止可视化。
欢迎关注公众号学习之后的深度学习连载部分~
 喜欢记得点在看哦,证明你来看过~
喜欢记得点在看哦,证明你来看过~