搜索

基于梯度下降算法求解线性回归

小白学视觉

共 5833字，需浏览 12分钟

 ·

2021-08-05 23:37

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达


01. 线性回归(Linear Regression)

梯度下降算法在机器学习方法分类中属于监督学习。利用它可以求解线性回归问题，计算一组二维数据之间的线性关系，假设有一组数据如下下图所示

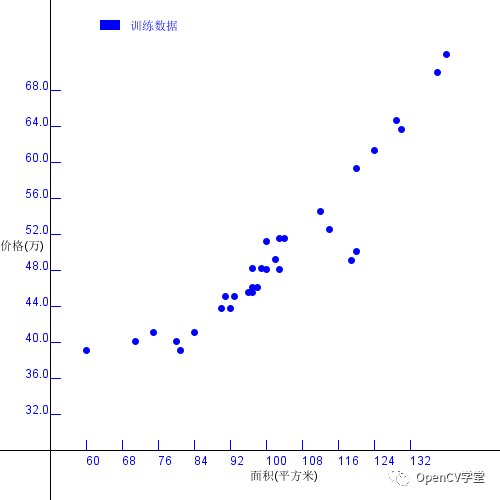
其中X轴方向表示房屋面积、Y轴表示房屋价格。我们希望根据上述的数据点，拟合出一条直线，能跟对任意给定的房屋面积实现价格预言，这样求解得到直线方程过程就叫线性回归，得到的直线为回归直线，数学公式表示如下:

02. 梯度下降


 


03. 代码实现各步

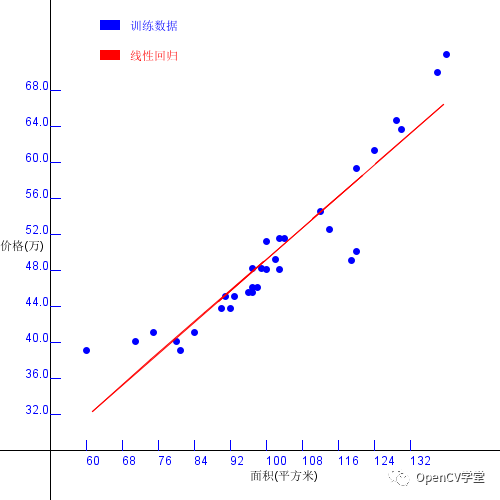
训练数据读入

  1. List<DataItem> items = new ArrayList<DataItem>();
  2. File f = new File(fileName);
  3. try {
  4.     if (f.exists()) {
  5.         BufferedReader br = new BufferedReader(new FileReader(f));
  6.         String line = null;
  7.         while((line = br.readLine()) != null) {
  8.             String[] data = line.split(",");
  9.             if(data != null && data.length == 2) {
  10.                 DataItem item = new DataItem();
  11.                 item.x = Integer.parseInt(data[0]);
  12.                 item.y = Integer.parseInt(data[1]);
  13.                 items.add(item);
  14.             }
  15.         }
  16.         br.close();
  17.     }
  18. } catch (IOException ioe) {
  19.     System.err.println(ioe);
  20. }
  21. return items;

归一化处理

  1. float min = 100000;
  2. float max = 0;
  3. for(DataItem item : items) {
  4.     min = Math.min(min, item.x);
  5.     max = Math.max(max, item.x);
  6. }
  7. float delta = max - min;
  8. for(DataItem item : items) {
  9.     item.x = (item.x - min) / delta;
  10. }

梯度下降

  1. int repetion = 1500;
  2. float learningRate = 0.1f;
  3. float[] theta = new float[2];
  4. Arrays.fill(theta, 0);
  5. float[] hmatrix = new float[items.size()];
  6. Arrays.fill(hmatrix, 0);
  7. int k=0;
  8. float s1 = 1.0f / items.size();
  9. float sum1=0, sum2=0;
  10. for(int i=0; i<repetion; i++) {
  11.     for(k=0; k<items.size(); k++ ) {
  12.         hmatrix[k] = ((theta[0] + theta[1]*items.get(k).x) - items.get(k).y);
  13.     }
  15.     for(k=0; k<items.size(); k++ ) {
  16.         sum1 += hmatrix[k];
  17.         sum2 += hmatrix[k]*items.get(k).x;
  18.     }
  20.     sum1 = learningRate*s1*sum1;
  21.     sum2 = learningRate*s1*sum2;
  23.     // 更新 参数theta
  24.     theta[0] = theta[0] - sum1;
  25.     theta[1] = theta[1] - sum2;
  26. }
  28. return theta;

价格预言 - theta表示参数矩阵

  1. float result = theta[0] + theta[1]*input;
  2. return result;

线性回归Plot绘制

  1. int w = 500;
  2. int h = 500;
  3. BufferedImage plot = new BufferedImage(w, h, BufferedImage.TYPE_INT_ARGB);
  4. Graphics2D g2d = plot.createGraphics();
  5. g2d.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);
  6. g2d.setPaint(Color.WHITE);
  7. g2d.fillRect(0, 0, w, h);
  8. g2d.setPaint(Color.BLACK);
  9. int margin = 50;
  10. g2d.drawLine(margin, 0, margin, h);
  11. g2d.drawLine(0, h-margin, w, h-margin);
  12. float minx=Float.MAX_VALUE, maxx=Float.MIN_VALUE;
  13. float miny=Float.MAX_VALUE, maxy=Float.MIN_VALUE;
  14. for(DataItem item : series1) {
  15.     minx = Math.min(item.x, minx);
  16.     maxx = Math.max(maxx, item.x);
  17.     miny = Math.min(item.y, miny);
  18.     maxy = Math.max(item.y, maxy);
  19. }
  20. for(DataItem item : series2) {
  21.     minx = Math.min(item.x, minx);
  22.     maxx = Math.max(maxx, item.x);
  23.     miny = Math.min(item.y, miny);
  24.     maxy = Math.max(item.y, maxy);
  25. }
  26. // draw X, Y Title and Aixes
  27. g2d.setPaint(Color.BLACK);
  28. g2d.drawString("价格(万)", 0, h/2);
  29. g2d.drawString("面积(平方米)", w/2, h-20);
  31. // draw labels and legend
  32. g2d.setPaint(Color.BLUE);
  33. float xdelta = maxx - minx;
  34. float ydelta = maxy - miny;
  35. float xstep = xdelta / 10.0f;
  36. float ystep = ydelta / 10.0f;
  37. int dx = (w - 2*margin) / 11;
  38. int dy = (h - 2*margin) / 11;
  40. // draw labels
  41. for(int i=1; i<11; i++) {
  42.     g2d.drawLine(margin+i*dx, h-margin, margin+i*dx, h-margin-10);
  43.     g2d.drawLine(margin, h-margin-dy*i, margin+10, h-margin-dy*i);
  44.     int xv = (int)(minx + (i-1)*xstep);
  45.     float yv = (int)((miny + (i-1)*ystep)/10000.0f);
  46.     g2d.drawString(""+xv, margin+i*dx, h-margin+15);
  47.     g2d.drawString(""+yv, margin-25, h-margin-dy*i);
  48. }
  50. // draw point
  51. g2d.setPaint(Color.BLUE);
  52. for(DataItem item : series1) {
  53.     float xs = (item.x - minx) / xstep + 1;
  54.     float ys = (item.y - miny) / ystep + 1;
  55.     g2d.fillOval((int)(xs*dx+margin-3), (int)(h-margin-ys*dy-3), 7,7);
  56. }
  57. g2d.fillRect(100, 20, 20, 10);
  58. g2d.drawString("训练数据", 130, 30);
  60. // draw regression line
  61. g2d.setPaint(Color.RED);
  62. for(int i=0; i<series2.size()-1; i++) {
  63.     float x1 = (series2.get(i).x - minx) / xstep + 1;
  64.     float y1 = (series2.get(i).y - miny) / ystep + 1;
  65.     float x2 = (series2.get(i+1).x - minx) / xstep + 1;
  66.     float y2 = (series2.get(i+1).y - miny) / ystep + 1;
  67.     g2d.drawLine((int)(x1*dx+margin-3), (int)(h-margin-y1*dy-3), (int)(x2*dx+margin-3), (int)(h-margin-y2*dy-3));
  68. }
  69. g2d.fillRect(100, 50, 20, 10);
  70. g2d.drawString("线性回归", 130, 60);
  73. g2d.dispose();
  74. saveImage(plot);


04. 总结

本文通过最简单的示例，演示了利用梯度下降算法实现线性回归分析，使用更新收敛的算法常被称为LMS(Least Mean Square)又叫Widrow-Hoff学习规则，此外梯度下降算法还可以进一步区分为增量梯度下降算法与批量梯度下降算法，这两种梯度下降方法在基于神经网络的机器学习中经常会被提及，对此感兴趣的可以自己进一步探索与研究。

下载1：OpenCV-Contrib扩展模块中文版教程
在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群


欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~


浏览 30
点赞
评论
收藏
分享

手机扫一扫分享

分享
举报
评论
图片
表情
推荐
梯度下降算法综述！
机器学习实验室
0
【深度学习】PyTorch 中的线性回归和梯度下降
机器学习初学者
0
如何理解梯度下降算法
AI入门学习
0
【机器学习基础】线性回归和梯度下降的初学者教程
机器学习初学者
0
梯度下降算法的工作原理
极市平台
0
各种 Optimizer 梯度下降优化算法总结
Datawhale
0
【机器学习基础】(二)：理解线性回归与梯度下降并做简单预测
机器学习初学者
0
各种梯度下降优化算法回顾和总结
Python学习与数据挖掘
0
简单聊聊梯度下降与反向传播算法
机器学习算法与Python实战
0
总结 | 各种Optimizer梯度下降优化算法回顾
目标检测与深度学习
0
点赞
评论
收藏
分享

手机扫一扫分享

分享
举报