常见的距离算法和相似度计算方法
点击下方卡片,关注“新机器视觉”公众号
重磅干货,第一时间送达
本文整理了常见的距离算法和相似度(系数)算法,并比较了欧氏距离和余弦距离间的不同之处。
1、常见的距离算法
>>> pdist = nn.PairwiseDistance(p=2)>>> input1 = torch.randn(100, 128)>>> input2 = torch.randn(100, 128)>>> output = pdist(input1, input2)
C代码包:emd.h, emd.c, emd.iOpenCV:实现了EMD api,pip install --upgrade setuptoolspip install numpy Matplotlibpip install opencv-pythonimport numpy as npimport cv#p、q是两个矩阵,第一列表示权值,后面三列表示直方图或数量p=np.asarray([[0.4,100,40,22],[0.3,211,20,2],[0.2,32,190,150],[0.1,2,100,100]],np.float32)q=np.array([[0.5,0,0,0],[0.3,50,100,80],[0.2,255,255,255]],np.float32)pp=cv.fromarray(p)qq=cv.fromarray(q)emd=cv.CalcEMD2(pp,qq,cv.CV_DIST_L2)
import numpy as npdef mashi_distance(x,y):print xprint y#马氏距离要求样本数要大于维数,否则无法求协方差矩阵#此处进行转置,表示10个样本,每个样本2维X=np.vstack([x,y])print XXT=X.Tprint XT#方法一:根据公式求解S=np.cov(X) #两个维度之间协方差矩阵SI = np.linalg.inv(S) #协方差矩阵的逆矩阵#马氏距离计算两个样本之间的距离,此处共有4个样本,两两组合,共有6个距离。n=XT.shape[0]d1=[]for i in range(0,n):for j in range(i+1,n):delta=XT[i]-XT[j]d=np.sqrt(np.dot(np.dot(delta,SI),delta.T))print dd1.append(d)
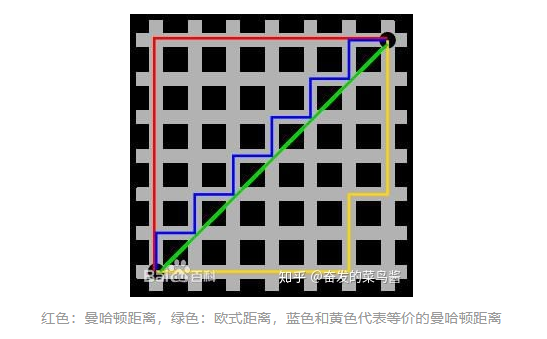
1、切比雪夫距离(Chebyshev Distance)
2、明可夫斯基距离(Minkowski Distance)
3、海明距离(Hamming distance)
4、马哈拉诺比斯距离(Mahalanobis Distance)
2、常见的相似度(系数)算法
>>> input1 = torch.randn(100, 128)>>> input2 = torch.randn(100, 128)>>> cos = nn.CosineSimilarity(dim=1, eps=1e-6)>>> output = cos(input1, input2)
import numpy as npx=np.random.random(8)y=np.random.random(8)#方法一:根据公式求解x_=x-np.mean(x)y_=y-np.mean(y)d1=np.dot(x_,y_)/(np.linalg.norm(x_)*np.linalg.norm(y_))#方法二:根据numpy库求解X=np.vstack([x,y])d2=np.corrcoef(X)[0][1]
>>> torch.nn.functional.kl_div(input, target, size_average=None, reduce=None, reduction='mean')>>> F.kl_div(q.log(),p,reduction='sum')#函数中的 p q 位置相反(也就是想要计算D(p||q),要写成kl_div(q.log(),p)的形式),而且q要先取 log#reduction 是选择对各部分结果做什么操作,
import numpy as npfrom scipy.spatial.distance import pdistx=np.random.random(8)>0.5y=np.random.random(8)>0.5x=np.asarray(x,np.int32)y=np.asarray(y,np.int32)#方法一:根据公式求解up=np.double(np.bitwise_and((x != y),np.bitwise_or(x != 0, y != 0)).sum())down=np.double(np.bitwise_or(x != 0, y != 0).sum())d1=(up/down)#方法二:根据scipy库求解X=np.vstack([x,y])d2=pdist(X,'jaccard')
import numpy as npdef tanimoto_coefficient(p_vec, q_vec):"""This method implements the cosine tanimoto coefficient metric:param p_vec: vector one:param q_vec: vector two:return: the tanimoto coefficient between vector one and two"""pq = np.dot(p_vec, q_vec)p_square = np.linalg.norm(p_vec)q_square = np.linalg.norm(q_vec)return pq / (p_square + q_square - pq)
#标准化互信息from sklearn import metricsif __name__ == '__main__':A = [1, 1, 1, 2, 3, 3]B = [1, 2, 3, 1, 2, 3]result_NMI=metrics.normalized_mutual_info_score(A, B)print("result_NMI:",result_NMI)
1、对数似然相似度/对数似然相似率
2、互信息/信息增益,相对熵/KL散度
3、信息检索——词频-逆文档频率(TF-IDF)
4、词对相似度——点间互信息
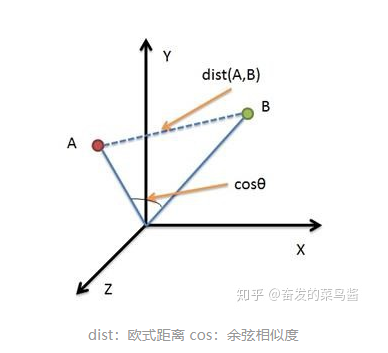
3、欧式距离vs余弦相似度
本文仅做学术分享,如有侵权,请联系删文。
评论
