一、 余弦相似概述

二、 余弦相似应用场景

原创文章检测：通过文本相似，可以检测公众号文章、论文等是否存在抄袭

垃圾邮件识别：如“诚聘淘宝兼职”、“诚聘打字员”、“文章代写”、“增值税发票”等这样的小广告满天飞，作为网站或者APP的风控，不可能简单的加几个关键字就能进行屏蔽的，一般常用的方法就是标注一部分典型的广告文本，与它相似度高的就进行屏蔽。

内容推荐系统：在腾讯新闻、微博、头条、知乎等，每一篇文章、帖子的下面都有一个推荐阅读，那就是根据一定算法计算出来的相似文章。

冗余新闻过滤：我们每天接触过量的信息，信息之间存在大量的重复，相似度可以帮我们删除这些重复内容，比如，大量相似新闻的过滤筛选。

可用于文本相似的方法非常多，比如基于字符的杰卡德相似、编辑距离相似、最长公共子串等，基于距离的相似也很多，比如汉明距离、欧几里得距离等。本文介绍的是余弦距离相似，比较简单，可以作为风控领域文本相似的入门。

废话不多说，先看一个案例，我们用三句话作为例子，我从自己的邮箱里面扒出来的垃圾邮件，具体步骤如下。

三、 计算文本余弦相似

第一步，分词。

第二步，列出所有的词（所有词的长度作为向量长度）

有，发票，加，薇，微，45357，正规，增值税

第三步，计算词频

A句子：有 1，发票 1，加 1，薇 1，微 0，45357 1，正规 0，增值税 0

B句子：有 1，发票 1，加 1，薇 0，微 1，45357 1，正规 0，增值税 0

C句子：有 0，发票 1，加 0，薇 0，微 0，45357 0，正规 1，增值税 1

第四步，写出词频向量。

A句子：[1, 1, 1, 1, 0, 1, 0 ,0]

B句子：[1, 1, 1, 0, 1, 1, 0 ,0]

C句子：[0, 1, 0, 0, 0, 0, 1 ,1]

到这里，问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段，都是从原点（0, 0, ...）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

以二维空间为例，上图的a和b是两个向量，我们要计算它们的夹角θ。根据初中知识，余弦定理告诉我们，可以用下面的公式求得：

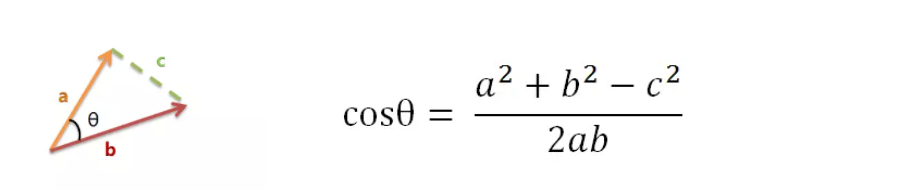
假定a向量是[x1, y1]，b向量是[x2, y2]，那么可以将余弦定理改写成下面的形式：

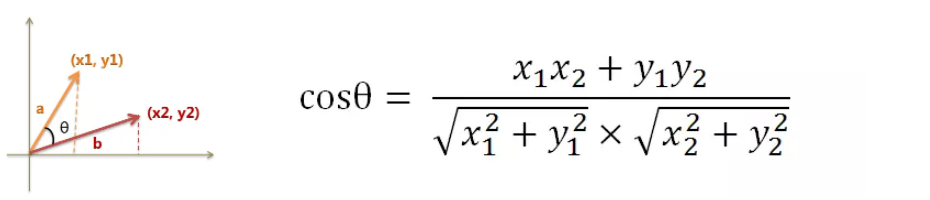
数学家已经证明，余弦的这种计算方法对n维向量也成立，假定A和B是两个n维向量，A是 [A1, A2, ..., An] ，B是 [B1, B2, ..., Bn] ，则A与B的夹角θ的余弦等于：

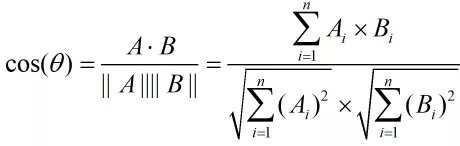
使用这个公式，我们就可以得到，句子A与句子B的夹角的余弦。

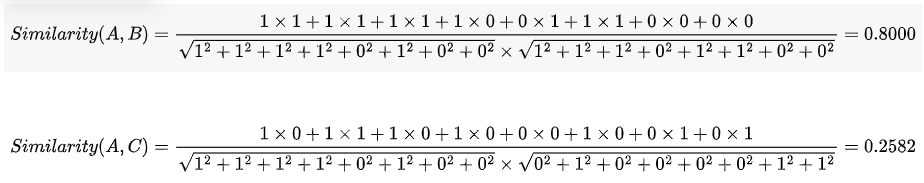
下面我们用Python代码计算看看

import numpy as npA = np.array([1, 1, 1, 1, 0, 1, 0 ,0])B = np.array([1, 1, 1, 0, 1, 1, 0 ,0])C = np.array([0, 1, 0, 0, 0, 0, 1 ,1])#定义相似计算函数def cos_simi(x,y):   num = x.dot(y.T)   denom = np.linalg.norm(x) * np.linalg.norm(y)   return num / denomcos_simi(A,B)0.7999999999999998cos_simi(A,C)0.2581988897471611cos_simi(B,C)0.2581988897471611

 ···  END  ···

↓长按关注本号、加我交流↓