【机器学习基础】机器学习距离与相似度计算
写在前面
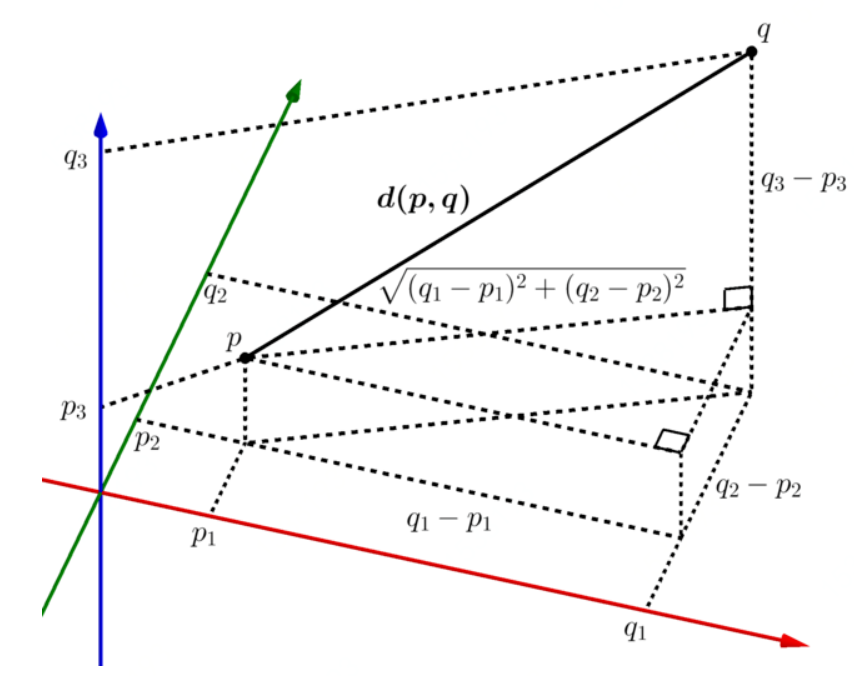
欧几里得距离
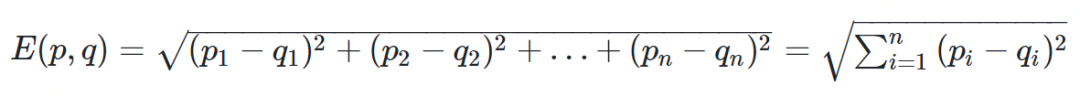

from math import *def euclidean_distance(x, y):return sqrt(sum(pow(a - b, 2) for a, b in zip(x, y)))print(euclidean_distance([0, 3, 4, 5], [7, 6, 3, -1]))
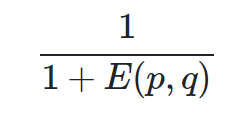
标准化欧式距离
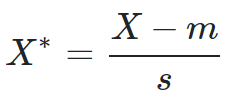
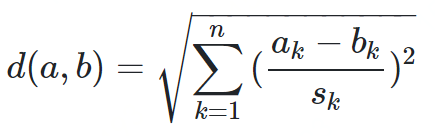
def normalized_euclidean(a, b):sumnum = 0for i in range(len(a)):avg = (a[i] - b[i]) / 2si = ((a[i] - avg) ** 2 + (b[i] - avg) ** 2) ** 0.5sumnum += ((a[i] - b[i]) / si) ** 2return sumnum ** 0.5
曼哈顿距离
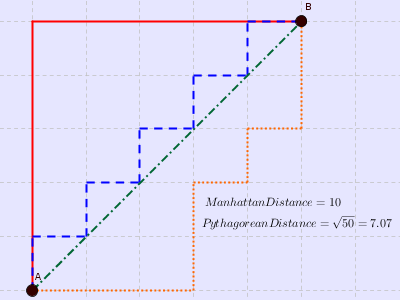

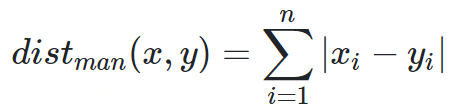
from math import *def manhattan_distance(x,y):return sum(abs(a-b) for a,b in zip(x,y))print(manhattan_distance([10,20,10],[10,20,20]))
汉明距离
“karolin” 和 “kathrin” 的汉明距离为(字符2 3 4替换) “karolin” 和 “kerstin” 的汉明距离为(字符1 3 4替换) 1011101 和 1001001 的汉明距离为(字符2 4替换) 2173896 和 2233796 的汉明距离为(字符1 2 4替换)
def hamming_distance(s1, s2):"""Return the Hamming distance between equal-length sequences"""if len(s1) != len(s2):raise ValueError("Undefined for sequences of unequal length")return sum(el1 != el2 for el1, el2 in zip(s1, s2))
赛切比雪夫距离

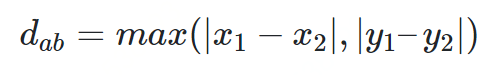
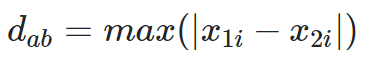
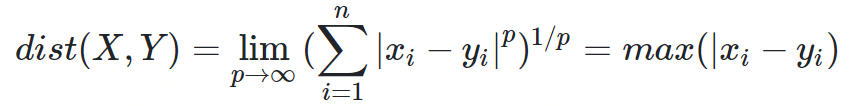
def chebyshev_distance(p, q):assert len(p) == len(q)return max([abs(x - y) for x, y in zip(p, q)])def chebyshev_distance_procedural(p, q):assert len(p) == len(q)d = 0for x, y in zip(p, q):d = max(d, abs(x - y))return d
马氏距离
方差:方差是标准差的平方,而标准差的意义是数据集中各个点到均值点距离的平均值。反应的是数据的离散程度。 协方差:标准差与方差是描述一维数据,当存在多维数据时,我们通常需要知道每个维数的变量中间是否存在关联。协方差就是衡量多维数据集中,变量之间相关性的统计量。如果两个变量之间的协方差为正值,则这两个变量之间存在正相关,若为负值,则为负相关。
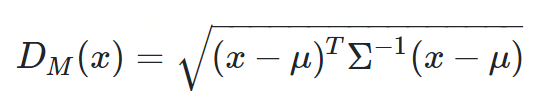
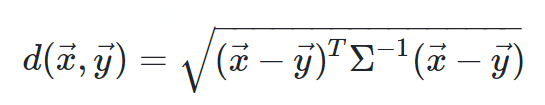
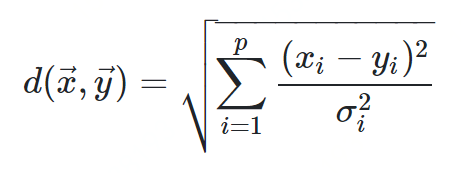
import pandas as pdimport scipy as spfrom scipy.spatial.distance import mahalanobisdatadict = {'country': ['Argentina', 'Bolivia', 'Brazil', 'Chile', 'Ecuador', 'Colombia', 'Paraguay', 'Peru', 'Venezuela'],'d1': [0.34, -0.19, 0.37, 1.17, -0.31, -0.3, -0.48, -0.15, -0.61],'d2': [-0.57, -0.69, -0.28, 0.68, -2.19, -0.83, -0.53, -1, -1.39],'d3': [-0.02, -0.55, 0.07, 1.2, -0.14, -0.85, -0.9, -0.47, -1.02],'d4': [-0.69, -0.18, 0.05, 1.43, -0.02, -0.7, -0.72, 0.23, -1.08],'d5': [-0.83, -0.69, -0.39, 1.31, -0.7, -0.75, -1.04, -0.52, -1.22],'d6': [-0.45, -0.77, 0.05, 1.37, -0.1, -0.67, -1.4, -0.35, -0.89]}pairsdict = {'country1': ['Argentina', 'Chile', 'Ecuador', 'Peru'],'country2': ['Bolivia', 'Venezuela', 'Colombia', 'Peru']}#DataFrame that contains the data for each countrydf = pd.DataFrame(datadict)#DataFrame that contains the pairs for which we calculate the Mahalanobis distancepairs = pd.DataFrame(pairsdict)#Add data to the country pairspairs = pairs.merge(df, how='left', left_on=['country1'], right_on=['country'])pairs = pairs.merge(df, how='left', left_on=['country2'], right_on=['country'])#Convert data columns to list in a single cellpairs['vector1'] = pairs[['d1_x','d2_x','d3_x','d4_x','d5_x','d6_x']].values.tolist()pairs['vector2'] = pairs[['d1_y','d2_y','d3_y','d4_y','d5_y','d6_y']].values.tolist()mahala = pairs[['country1', 'country2', 'vector1', 'vector2']]#Calculate covariance matrixcovmx = df.cov()invcovmx = sp.linalg.inv(covmx)#Calculate Mahalanobis distancemahala['mahala_dist'] = mahala.apply(lambda x: (mahalanobis(x['vector1'], x['vector2'], invcovmx)), axis=1)mahala = mahala[['country1', 'country2', 'mahala_dist']]
两点之间的马氏距离与原始数据的测量单位无关(不受量纲的影响) 标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同 可以排除变量之间的相关性的干扰 满足距离的四个基本公理:非负性、自反性、对称性和三角不等式 缺点是夸大了变化微小的变量的作用
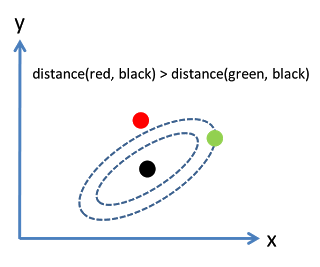
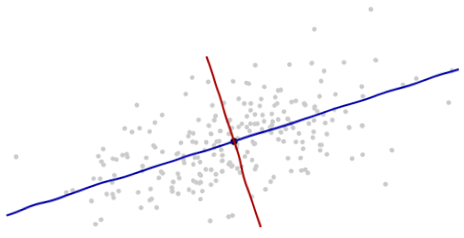
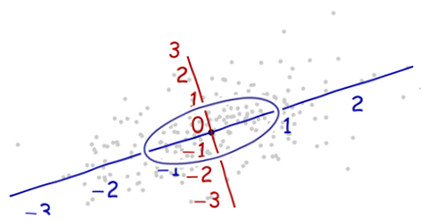
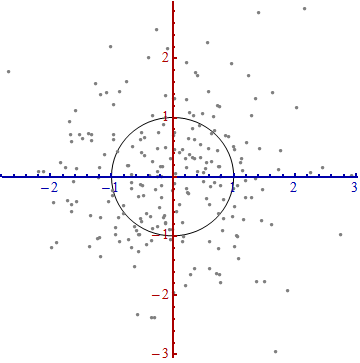
沿着新坐标轴的单位向量是协方差矩阵的特征向量。注意到没有变形的椭圆,变成圆形后沿着特征向量用标准差(协方差的平方根)将距离长度分割。 坐标轴扩展的量是协方差矩阵的逆的特征值(平方根),同理的,坐标轴缩小的量是协方差矩阵的特征值。所以,点越分散,需要的将椭圆转成圆的缩小量就越多。 尽管上述的操作可以用到任何数据上,但是对于多元正态分布的数据表现更好。在其他情况下,点的平均值或许不能很好的表示数据的中心,或者数据的“脊椎”(数据的大致趋势方向)不能用变量作为概率分布测度来准确的确定。 原始坐标系的平移、旋转,以及坐标轴的伸缩一起形成了仿射变换(affine transformation)。除了最开始的平移之外,其余的变换都是基底变换,从原始的一个变为新的一个。 在新的坐标系中,多元正态分布像是标准正太分布,当将变量投影到任何一条穿过原点的坐标轴上。特别是,在每一个新的坐标轴上,它就是标准正态分布。从这点出发来看,多元正态分布彼此之实质性的差异就在于它们的维度。
兰氏距离
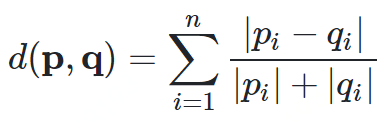
def canberra_distance(p, q):n = len(p)distance = 0for i in n:if p[i] == 0 and q[i] == 0:distance += 0else:distance += abs(p[i] - q[i]) / (abs(p[i]) + abs(q[i]))return distance
闵科夫斯基距离
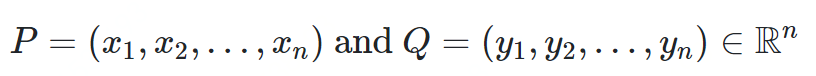
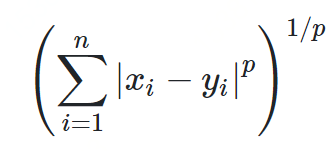


将各个分量的量纲(scale),也就是“单位”当作相同看待了 没有考虑各个分量的分布(期望,方差等)可能是不同的
def minkowski_distance(p, q, n):assert len(p) == len(q)return sum([abs(x - y) ^ n for x, y in zip(p, q)]) ^ 1 / ndef minkowski_distance_procedural(p, q, n):assert len(p) == len(q)s = 0for x, y in zip(p, q):s += abs(x - y) ^ nreturn s ^ (1 / n)
编辑距离
sitten (k→s) sittin (e→i) sitting (→g)
import Levenshteintexta = 'Coggle'textb = 'Google'print Levenshtein.distance(texta,textb)
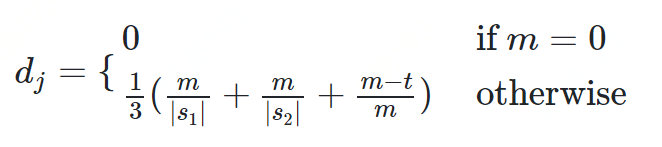
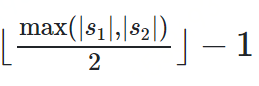
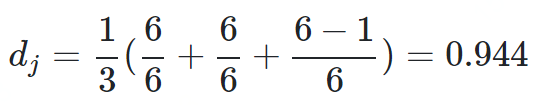
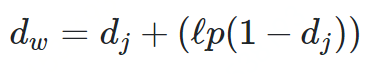
dj是两个字符串的Jaro Distance ι是前缀的相同的长度,但是规定最大为4 p则是调整分数的常数,规定不能超过25,不然可能出现dw大于1的情况,Winkler将这个常数定义为0.1
dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961去除停用词(主要是标点符号的影响) 针对中文进行分析,按照词比较是不是要比按照字比较效果更好?
余弦相似度
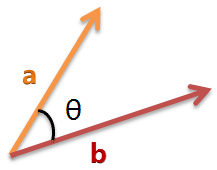
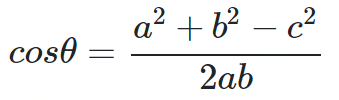
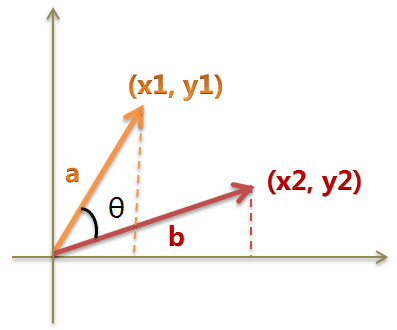
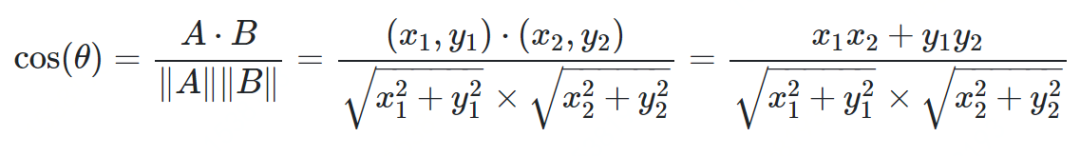
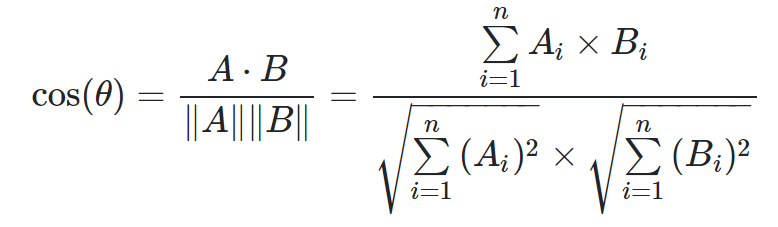
from math import *def square_rooted(x):return round(sqrt(sum([a*a for a in x])),3)def cosine_similarity(x,y):numerator = sum(a*b for a,b in zip(x,y))denominator = square_rooted(x)*square_rooted(y)return round(numerator/float(denominator),3)print(cosine_similarity([3, 45, 7, 2], [2, 54, 13, 15]))
杰卡德相似度
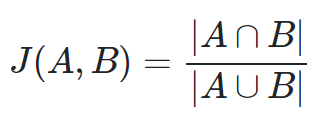
def jaccard_sim(a, b):unions = len(set(a).union(set(b)))intersections = len(set(a).intersection(set(b)))return intersections / unionsa = ['x', 'y']b = ['x', 'z', 'v']print(jaccard_sim(a, b))
杰卡德距离
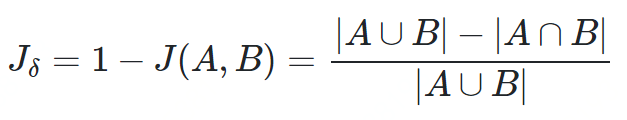
def jaccard_similarity(x,y):intersection_cardinality = len(set.intersection(*[set(x), set(y)]))union_cardinality = len(set.union(*[set(x), set(y)]))return intersection_cardinality/float(union_cardinality)print(jaccard_similarity([0,1,2,5,6],[0,2,3,5,7,9]))
Dice系数
Dice距离用于度量两个集合的相似性,因为可以把字符串理解为一种集合,因此Dice距离也会用于度量字符串的相似性。此外,Dice系数的一个非常著名的使用即实验性能评测的F1值。Dice系数定义如下:
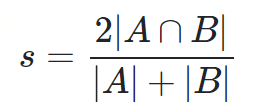
其中分子是A与B的交集数量的两倍,分母为X和Y的长度之和,所以他的范围也在0到1之间。从公式看,Dice系数和Jaccard非常的类似。Jaccard是在分子和分母上都减去了|A∩B|。
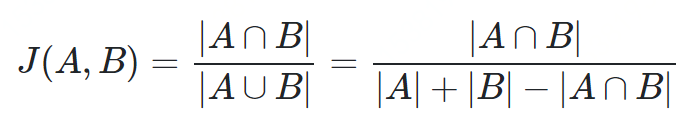
与Jaccard不同的是,相应的差异函数
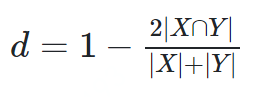
不是一个合适的距离度量措施,因为它没有三角形不等性的性质。例如给定 {a}, {b}, 和 {a,b}, 前两个集合的距离为1, 而第三个集合和其他任意两个集合的距离为三分之一。
与Jaccard类似, 集合操作可以用两个向量A和B的操作来表示:
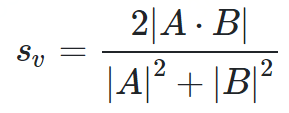
def dice_coefficient(a, b):"""dice coefficient 2nt/na + nb."""a_bigrams = set(a)b_bigrams = set(b)overlap = len(a_bigrams & b_bigrams)return overlap * 2.0/(len(a_bigrams) + len(b_bigrams))
往期精彩回顾
获取本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/y7uvZF6
本站qq群704220115。
加入微信群请扫码:
评论