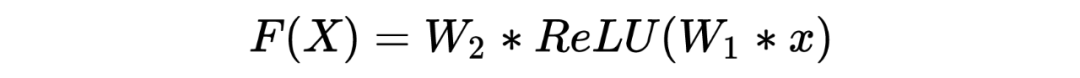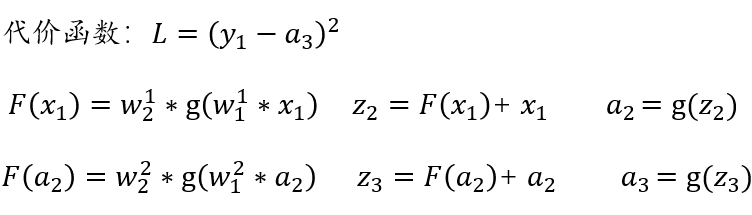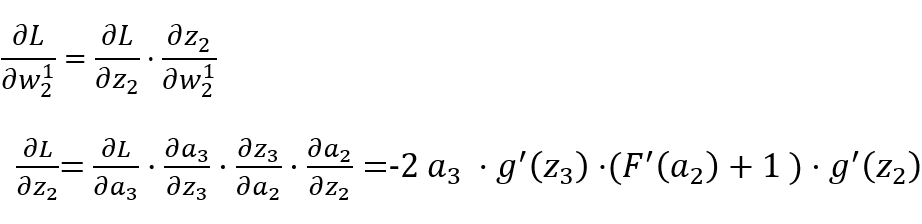可逆神经网络(Invertible Neural Networks)详细解析:让神经网络更加轻量化

来源:PaperWeekly 本文约3600字,建议阅读7分钟
本文以可逆残差网络(The Reversible Residual Network: Backpropagation Without Storing Activations)作为基础进行分析。
因为编码和解码使用相同的参数,所以 model 是轻量级的。可逆的降噪网络 InvDN 只有 DANet 网络参数量的 4.2%,但是 InvDN 的降噪性能更好。 由于可逆网络是信息无损的,所以它能保留输入数据的细节信息。 无论网络的深度如何,可逆网络都使用恒定的内存来计算梯度。
import torch
from torchvision import models
from torchsummary import summary
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
vgg = models.vgg16().to(device)
summary(vgg, (3, 224, 224))
结果:
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 64, 224, 224] 1,792
ReLU-2 [-1, 64, 224, 224] 0
Conv2d-3 [-1, 64, 224, 224] 36,928
ReLU-4 [-1, 64, 224, 224] 0
MaxPool2d-5 [-1, 64, 112, 112] 0
Conv2d-6 [-1, 128, 112, 112] 73,856
ReLU-7 [-1, 128, 112, 112] 0
Conv2d-8 [-1, 128, 112, 112] 147,584
ReLU-9 [-1, 128, 112, 112] 0
MaxPool2d-10 [-1, 128, 56, 56] 0
Conv2d-11 [-1, 256, 56, 56] 295,168
ReLU-12 [-1, 256, 56, 56] 0
Conv2d-13 [-1, 256, 56, 56] 590,080
ReLU-14 [-1, 256, 56, 56] 0
Conv2d-15 [-1, 256, 56, 56] 590,080
ReLU-16 [-1, 256, 56, 56] 0
MaxPool2d-17 [-1, 256, 28, 28] 0
Conv2d-18 [-1, 512, 28, 28] 1,180,160
ReLU-19 [-1, 512, 28, 28] 0
Conv2d-20 [-1, 512, 28, 28] 2,359,808
ReLU-21 [-1, 512, 28, 28] 0
Conv2d-22 [-1, 512, 28, 28] 2,359,808
ReLU-23 [-1, 512, 28, 28] 0
MaxPool2d-24 [-1, 512, 14, 14] 0
Conv2d-25 [-1, 512, 14, 14] 2,359,808
ReLU-26 [-1, 512, 14, 14] 0
Conv2d-27 [-1, 512, 14, 14] 2,359,808
ReLU-28 [-1, 512, 14, 14] 0
Conv2d-29 [-1, 512, 14, 14] 2,359,808
ReLU-30 [-1, 512, 14, 14] 0
MaxPool2d-31 [-1, 512, 7, 7] 0
Linear-32 [-1, 4096] 102,764,544
ReLU-33 [-1, 4096] 0
Dropout-34 [-1, 4096] 0
Linear-35 [-1, 4096] 16,781,312
ReLU-36 [-1, 4096] 0
Dropout-37 [-1, 4096] 0
Linear-38 [-1, 1000] 4,097,000
================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.57
Forward/backward pass size (MB): 218.59
Params size (MB): 527.79
Estimated Total Size (MB): 746.96
----------------------------------------------------------------
接下来我将先从可逆神经网络讲起,然后是神经网络的反向传播,最后是标准残差网络。对反向传播算法和标准残差网络比较熟悉的小伙伴,可以只看第一节:可逆神经网络。如果各位小伙伴不熟悉反向传播算法和标准残差网络,建议先看第二节:反向传播(BP)算法和第三节:残差网络(Residual Network)。本文1.2和1.3.4摘录自 @阿亮。
可逆神经网络
可逆网络具有的性质:
网络的输入、输出的大小必须一致。 网络的雅可比行列式不为 0。
1.1 什么是雅可比行列式?



1.2 雅可比行列式与神经网络的关系
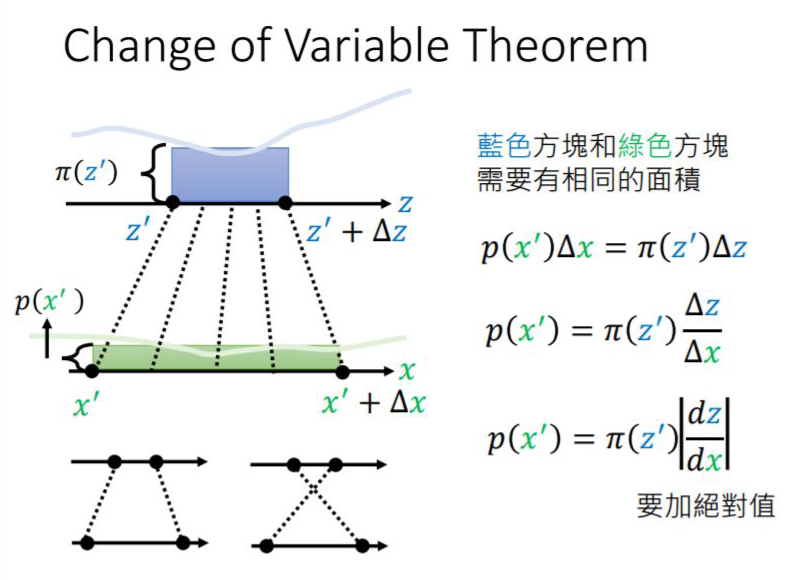
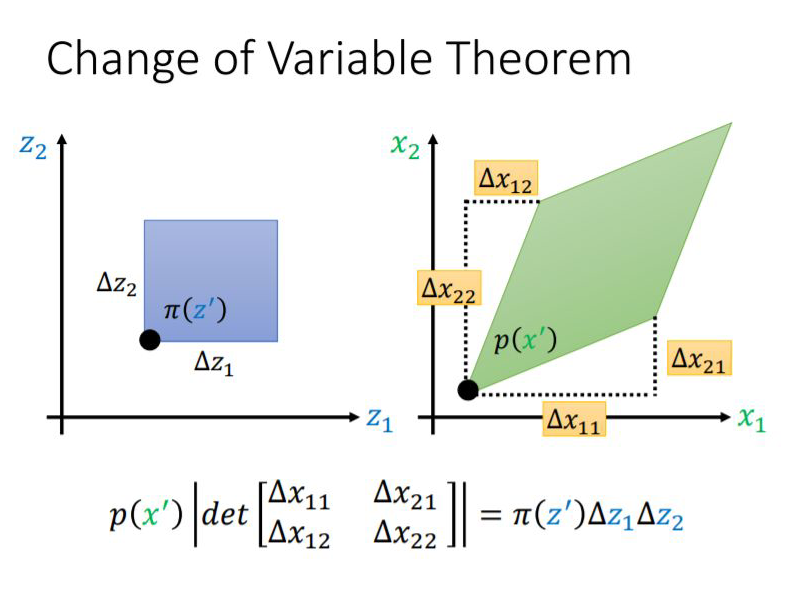
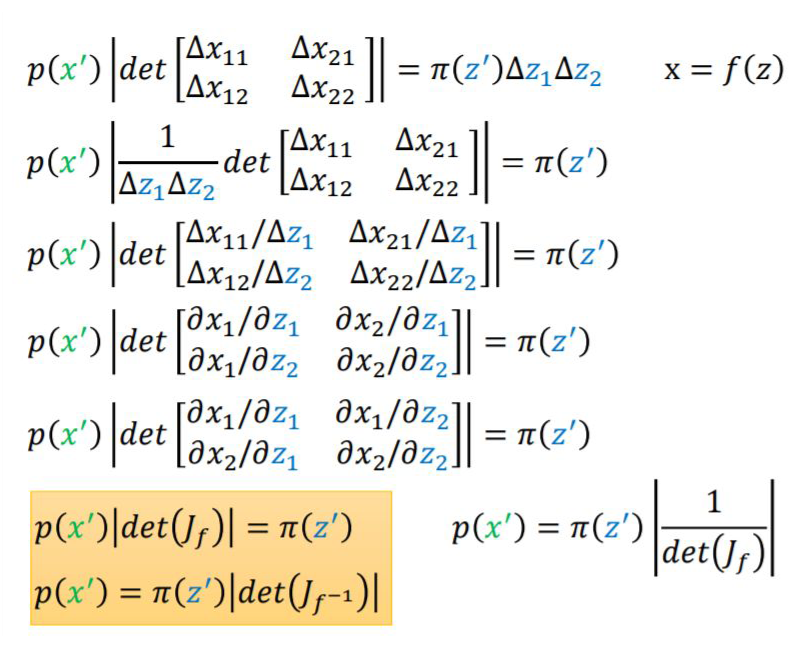
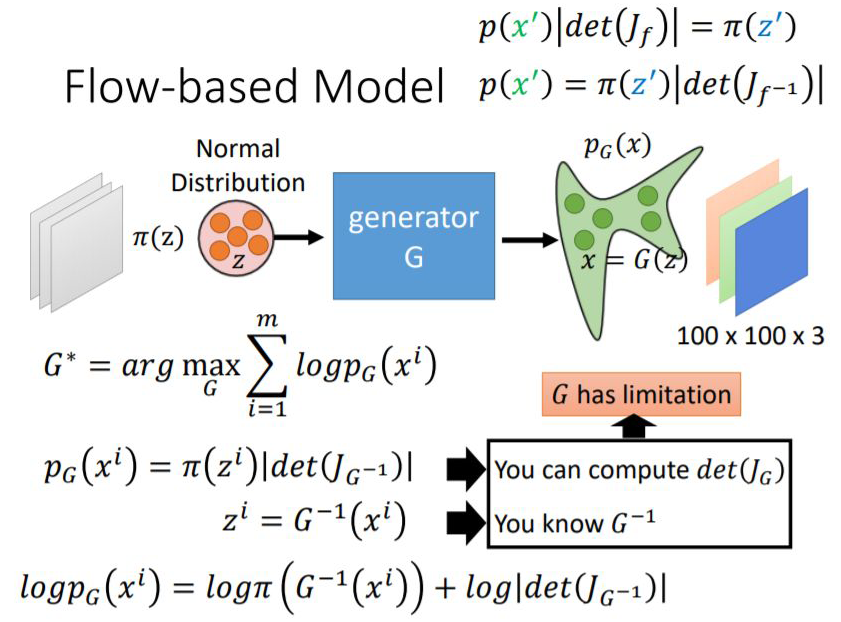
其实这里跟矩阵运算很像,矩阵可逆的条件也是矩阵的雅可比行列式不为 0,雅可比矩阵可以理解为矩阵的一阶导数。
假设可逆网络的表达式为:
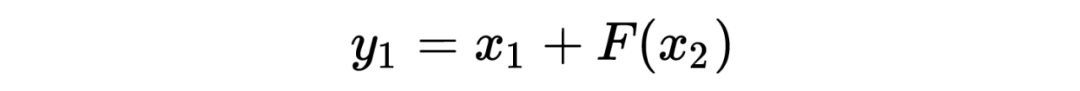
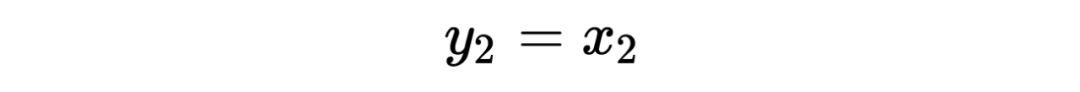
它的雅可比矩阵为:
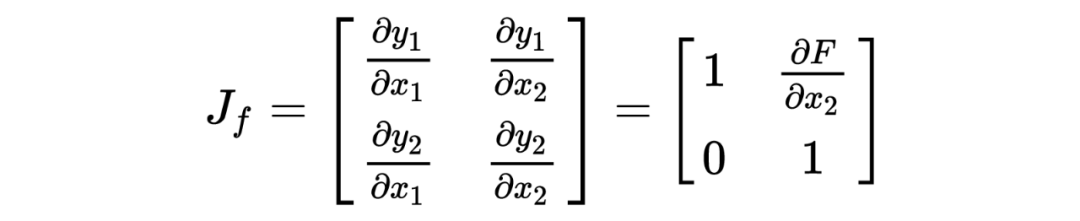
1.3 可逆残差网络(Reversible Residual Network)

论文标题:
The Reversible Residual Network: Backpropagation Without Storing Activations
论文链接:
https://arxiv.org/abs/1707.04585
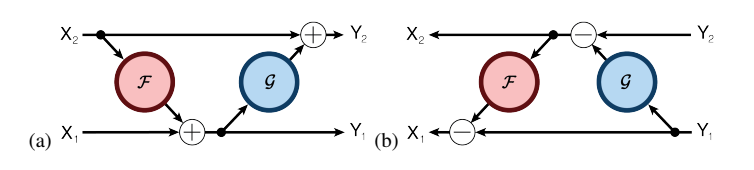
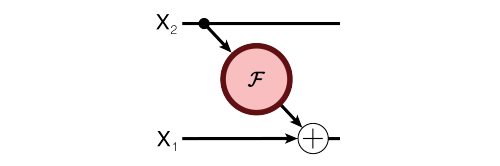
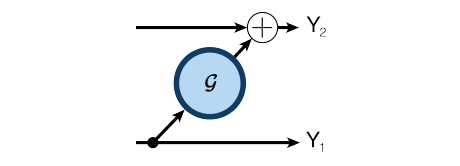
多伦多大学的 Aidan N.Gomez 和 Mengye Ren 提出了可逆残差神经网络,当前层的激活结果可由下一层的结果计算得出,也就是如果我们知道网络层最后的结果,就可以反推前面每一层的中间结果。这样我们只需要存储网络的参数和最后一层的结果即可,激活结果的存储与网络的深度无关了,将大幅减少显存占用。令人惊讶的是,实验结果显示,可逆残差网络的表现并没有显著下降,与之前的标准残差网络实验结果基本旗鼓相当。
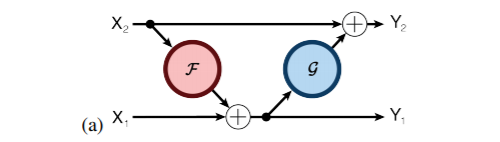
公式表示:
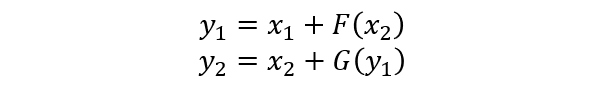
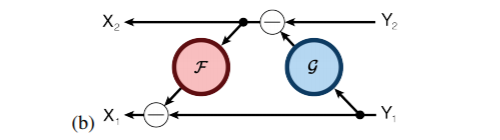
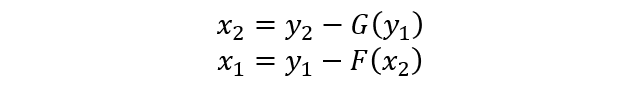
1.3.2 不用存储激活结果的反向传播
为了更好地计算反向传播的步骤,我们修改一下上述正向计算和逆向计算的公式:
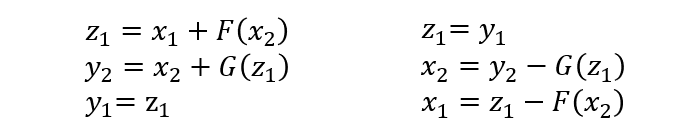

1.3.3 计算开销
一个 N 个连接的神经网络,正向计算的理论加乘开销为 N,反向传播求导的理论加乘开销为 2N(反向求导包含复合函数求导连乘),而可逆网络多一步需要反向计算输入值的操作,所以理论计算开销为 4N,比普通网络开销约多出 33% 左右。但是在实际操作中,正向和反向的计算开销在 GPU 上差不多,可以都理解为 N。那么这样的话,普通网络的整体计算开销为 2N,可逆网络的整体开销为 3N,也就是多出了约 50%。
1.3.4 雅可比行列式的计算
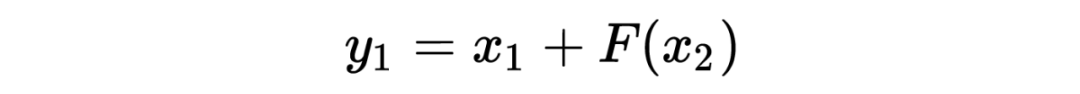
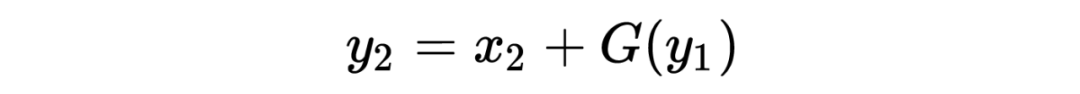
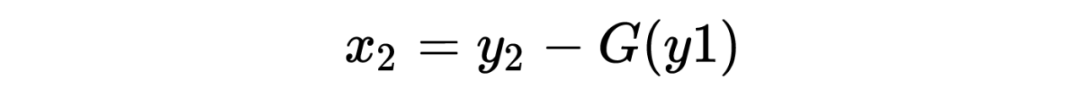

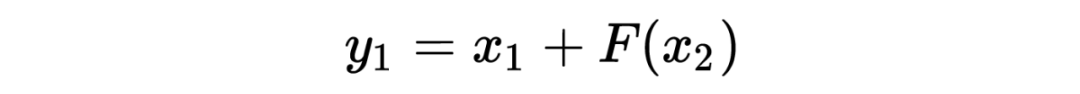
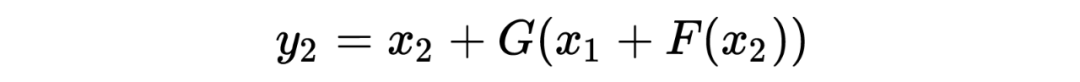

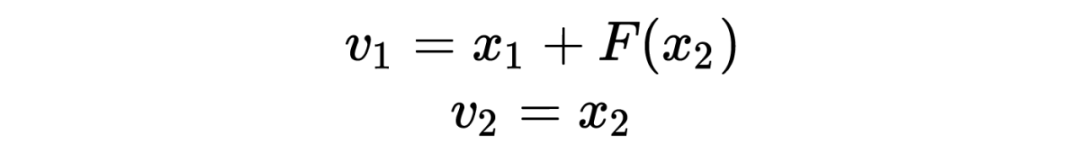
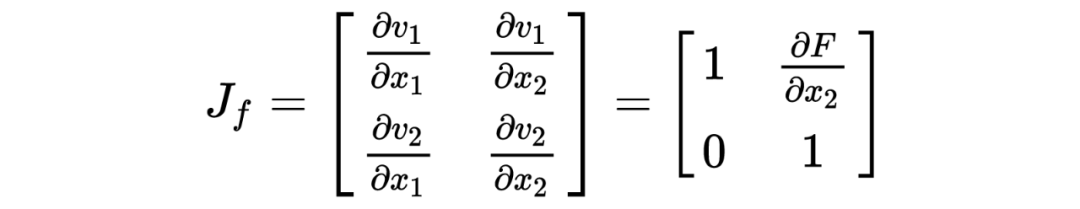
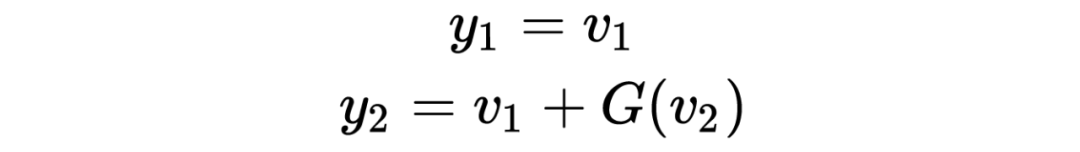
因为是对偶的形式,所以这里的行列式也为 1.
反向传播(BP)算法

x1,x2,x3:表示 3 个输入层节点。 :表示从 t-1 层到 t 层的权重参数,j 表示 t 层的第 j 个节点,i 表示 t-1 层的第 i 个节点。 :表示 t 层的第 i 个激活后输出结果。 g(x):表示激活函数。
隐藏层(网络的第二层)

输出层(网络的最后一层)
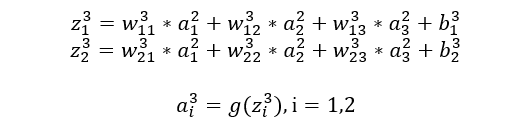
以平方误差来计算反向传播的过程,代价函数表示如下:
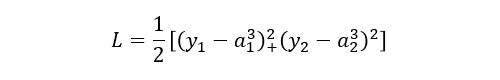
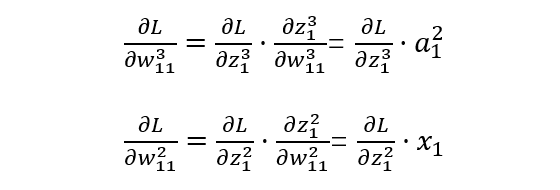
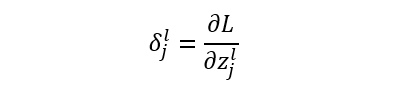
l=2,3 表示第几层,j 表示某一层的第几个节点。替换表示后如下:
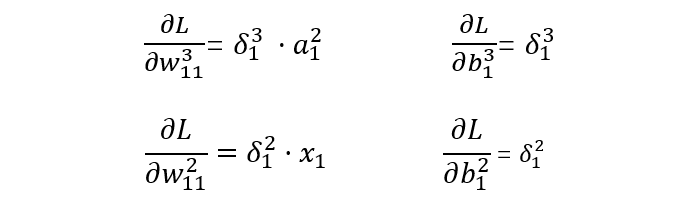
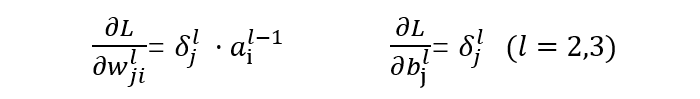
从上述公式可以看出,如果神经单元误差 δ 可以求出来,那么总误差对每一层的权重 w 和偏置 b 的偏导数就可以求出来,接下来就可以利用梯度下降法来优化参数了。
求解每一层的 δ:
输出层
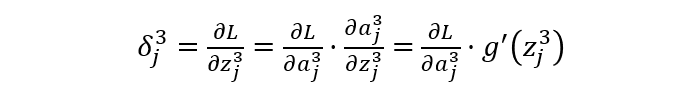
隐藏层
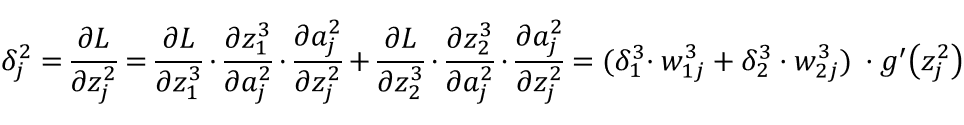

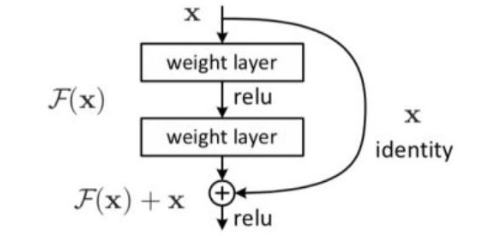
残差网络(Residual Network)
残差网络主要可以解决两个问题(其结构如下图):
1)梯度消失问题;
2)网络退化问题。