图神经网络概述：Graph Neural Networks-技术圈

本文参照以下两篇blog，这两篇应该是目前介绍GNN和GCN最好的blog了。

https://distill.pub/2021/gnn-intro/

https://distill.pub/2021/understanding-gnns/

讲图神经网络(GNN)之前，先介绍一下什么是graph，为什么需要graph，以及graph有什么问题，然后介绍一下如何用GNN处理graph问题，最后从GNN推广到GCN。

Graph

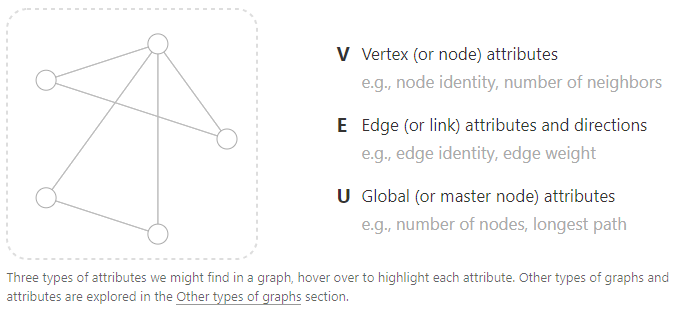
图由Vertex(V)、Edge(E)和Global(U)三部分构成。V可以表示为node identity或者number of neighbors，E可以表示为edge identity或者edge weight，U可以表示为number of nodes或者longest path。

为了进一步描述每一个node、edge和entire graph，可以把信息存储在graph的每个部分中。其实就是把信息以embedding的方式存储。

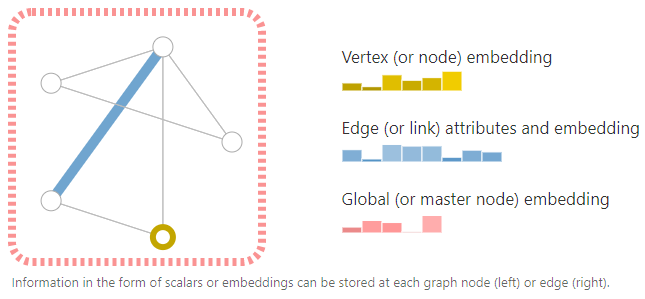
还可以通过edge的方向性(有向的、无向的)来构建特殊的图。

Graphs and where to find them

graph data在生活中无处不在，比如最常见的image和text都可以认为是graph data的一种特例，还有其他一些场景也可以用graph data表达。

Images as graphs

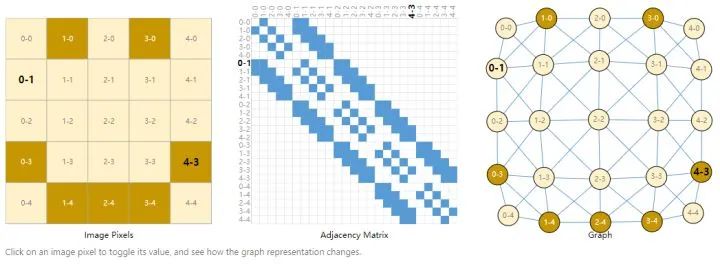
图片的位置可以表示成(列数-行数)的形式，将图片构建成adjacency matrix，蓝色块表示pixel和pixel之间相临，无方向性，画成graph就是右边图片的形式。

Text as graphs

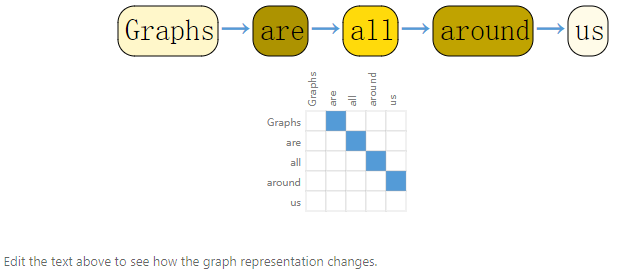
文本也可以构建成adjacency matrix，跟图片不一样的是，文本是一个有向图，每个词只跟前一个词相连接，并且有方向性。

其他还有比如分子、社交网络、学术引用网络等等都可以构建成graph。

What types of problems have graph structured data?

graph可以处理graph-level、node-level和edge-level三种层面的问题。

Graph-level task

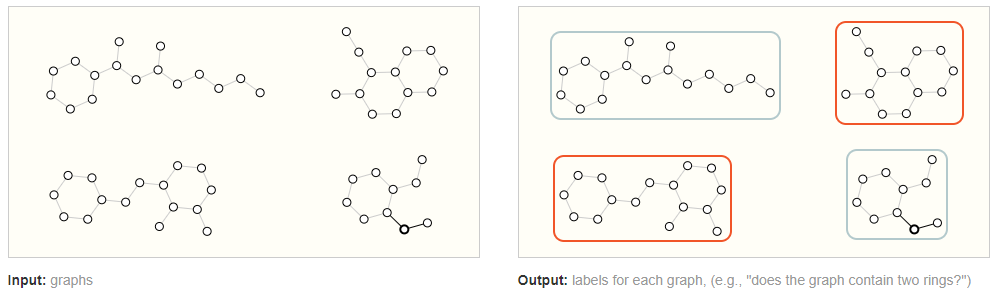
输入graph，输出整个graph的类别。在图像中，和图像分类任务类似；在文本中，和句子情感分析类似。

Node-level task

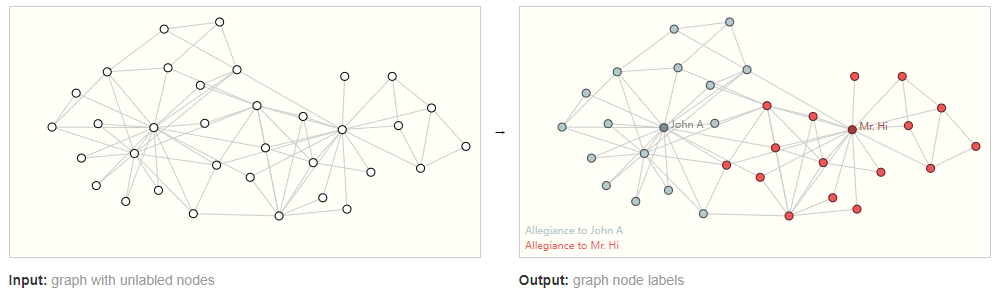
输入node不带类别的graph，输出每个node的类别。在图像中，和语义分割类似；在文本中，和词性分类类似。

Edge-level task

edge-level任务用来预测node之间的相互关系。如下图所示，先将不同部分分割出来，然后判断不同部分的相互关系。构建成graph就是对edge进行类别预测。

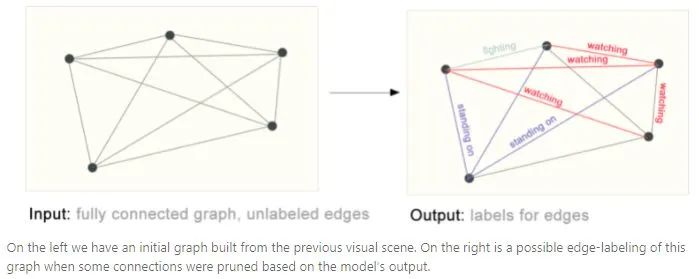
The challenges of using graphs in machine learning

如何用神经网络处理graph任务呢？

第一步是考虑如何表示和神经网络相兼容的图。graph最多有4种想要预测的信息：node、edge、global-context和connectivity。前3个相对容易，比如可以用一个 $Node_i$ 表示存储了第i个node的特征矩阵N。然而connectivity的表示要复杂的多，最直接的方式是构建邻接矩阵，但是空间效率很低，可能会产生非常稀疏的邻接矩阵。

还有一个问题是，许多邻接矩阵可以编码相同的连通性，但是不能保证这些不同的矩阵在神经网络中会产生相同的结果(也就是说，它们不是置换不变的)。

一种优雅而高效表示稀疏矩阵的方法是用邻接表。edge $e_k$ 表示节点 $n_i$ 和 $n_j$ 之间的连通性，在邻接表的第k项中表示为一个元组(i,j)。

以一个graph的邻接表为例，如下图所示:

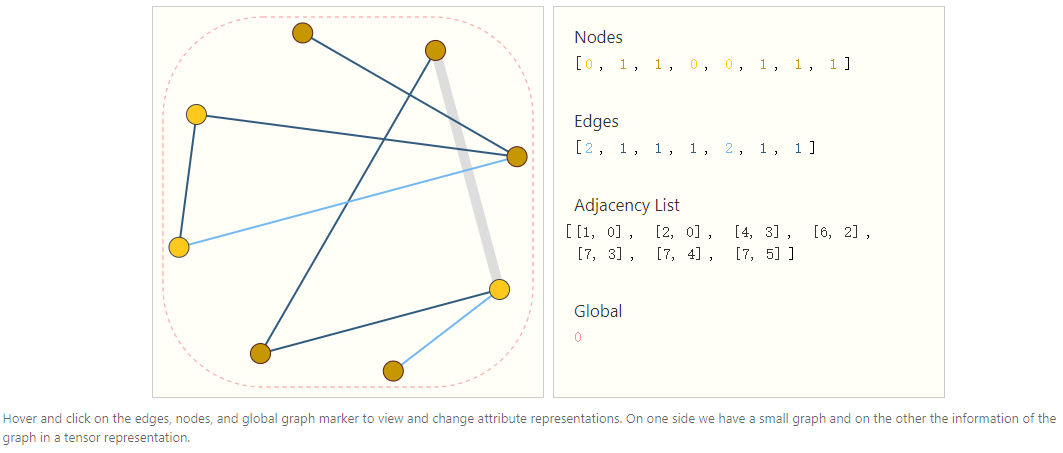
Graph Neural Networks

通过上面的描述，graph可以通过置换不变的邻接表表示，那么可以设计一个graph neural networks(GNN)来解决graph的预测任务。

The simplest GNN

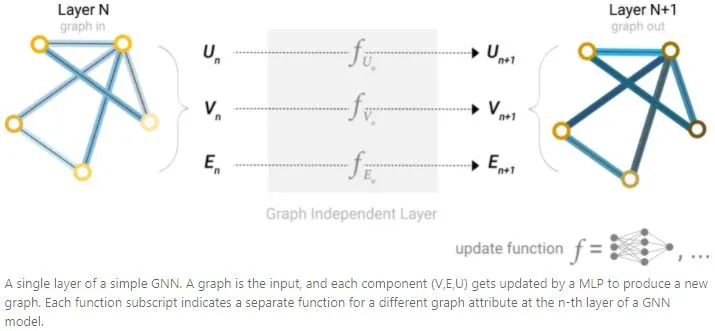
从最简单的GNN开始，更新所有graph的属性(nodes(V)，edges(E)，global(U))作为新的embedding，但是不使用graph的connectivity。

GNN对graph的每个组件分开使用MLP，称为GNN layer。对于每个node vetor，使用MLP后返回一个learned node-vector，同理edge会返回一个learned edge embedding，global会返回一个global embedding。

和CNN类似，GNN layer可以堆叠起来组成GNN。由于GNN layer不更新输入graph的connectivity，所有输出graph的邻接表跟输入图相同。但是通过GNN layer，node、edge和global-context的embedding已经更新。

GNN Predictions by Pooling Information

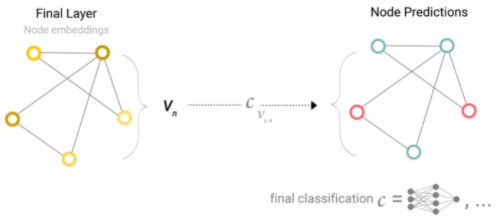
如果想用GNN做二分类任务，那么可以用一个linear classifier对graph进行分类。

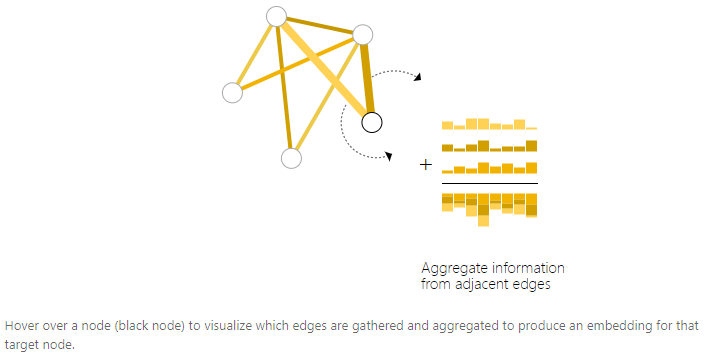
然而，有时候信息只储存在edge中，那么就需要从edge收集信息转移到node用于预测，这个过程称之为pooling。

Pooling过程有两个步骤：

1.对于要pooling的每一项(上图一行中的一列)，收集它们的embedding并且concat到一个矩阵中（上图中的一行）。

2.收集的embedding通过求和操作进行聚合。

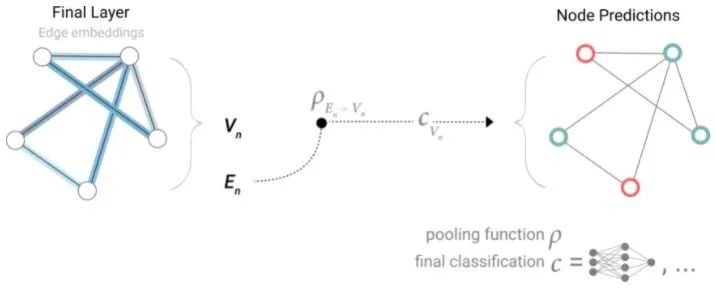
因此，如果只有edge-level的特征，可以通过pooling传递信息来预测node(上图虚线表示pooling传递信息给node，然后进行二分类)。

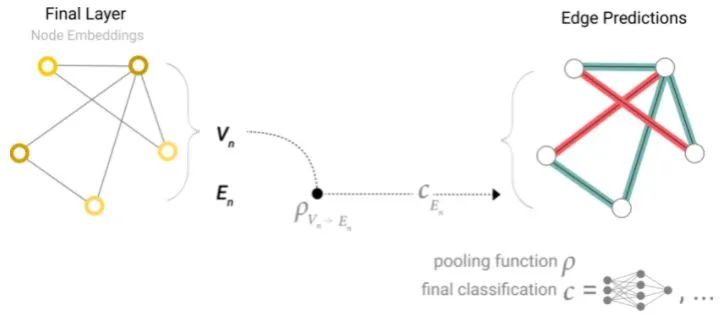
同理，如果只有node-level的特征，可以通过pooling传递信息来预测edge。类似CV中的global average pooling。

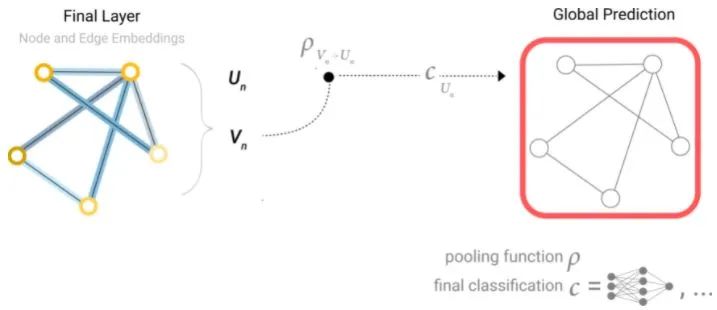
同理，可以通过node-level的特征预测global。

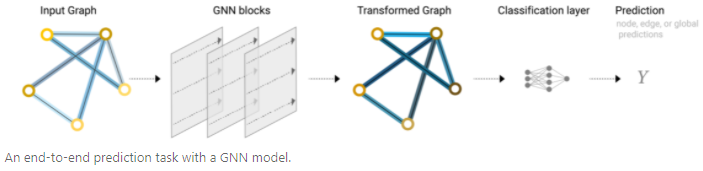
和CNN类似，通过GNN blocks可以构建出一个end-to-end的GNN。

需要注意的是，在这个最简单的GNN中，没有在GNN layer使用graph的connectivity。每个node、每个edge以及global-context都是独立处理的，只在聚合信息进行预测的时候使用了connectivity。

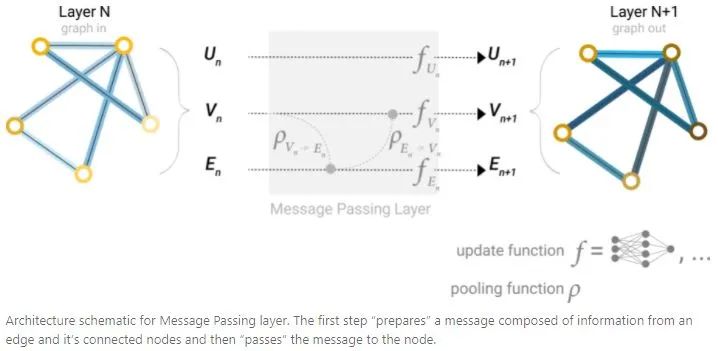
Passing messages between parts of the graph

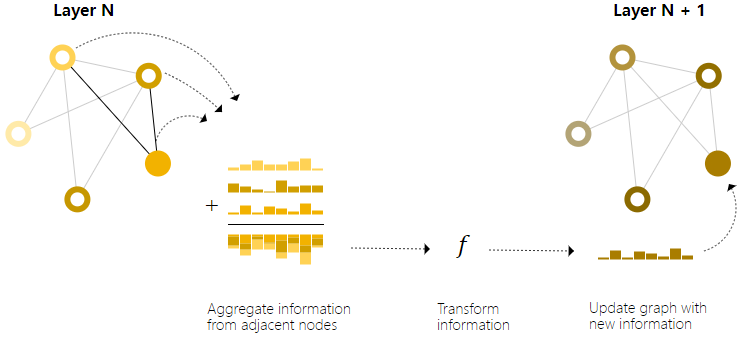
为了使learned embedding感知到graph的connectivity，可以在GNN layer使用pooling构建出更加复杂的GNN(和convlution类似)。可以使用message passing实现，相邻node或者edge可以交换信息，并且影响彼此的embedding更新。

Message passing过程有三个步骤：

1.对于graph的每个node，收集所有相邻node的embedding。

2.通过相加操作聚合所有message。

3.所有聚合的message都通过一个update function传递(通常使用一个可学习的神经网络)。

这些步骤是利用graph的connectivity的关键。在GNN layer中构建更精细的message passing变体，可以获得表达和能力更强的GNN模型。

通过堆叠的message passing GNN layer，一个node可以引入整个graph的信息：在三层GNN layer之后，一个node可以获得3步远的node信息。

对最简单的GNN范式进行更新，增加一个message passing操作:

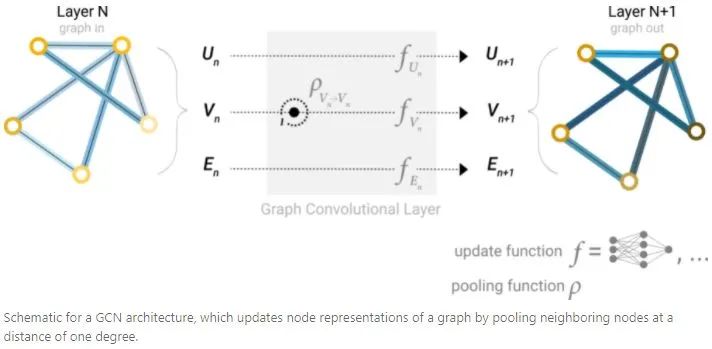
Learning edge representations

通过meassage passing，可以在GNN layer的node和edge之间共享信息。可以像之前使用相邻node信息一样，先将edge信息pooling，然后用update function转化并且存储，从而聚合来自相邻edge的信息。

然而，存储在graph中的node和edge信息不一定具有相同的大小或形状，因此不能立刻知道如何将它们组合起来。一种方法是学习从node空间到edge空间的线性映射，或者，可以在update function之前将它们concat在一起。

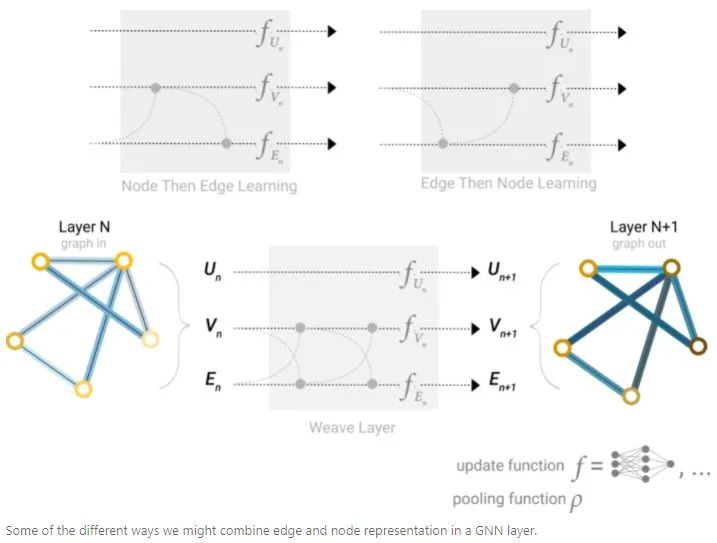
在构造GNN时，需要设计更新哪些graph属性以及更新顺序。比如可以使用weave的方式进行更新，node to node(linear)，edge to edge(linear)，node to edge(edge layer)，edge to node(node layer)。

Adding global representations

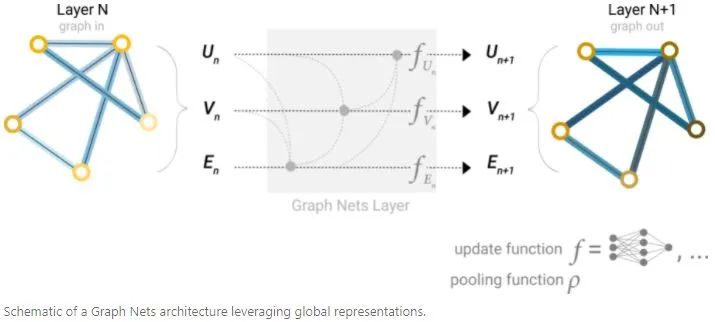
上面描述的GNN模型还有一个缺陷：在graph中，距离很远的node无法有效的传递信息，对于一个node，如果有k个layer，那么信息传递的距离最多是k步，这对于依赖相距很远的node信息的预测任务来说，是比较严重的问题。一种解决办法是让所有node可以相互传递信息，但是对于大的graph来说，计算量会非常昂贵。另一种解决办法是使用graph(U)的全局表示，称为master node或者context vector。这个全局的context vector可以连接到网络的所有node和edge，可以作为它们之间信息传递的桥梁，构建出一个graph的整体表示。

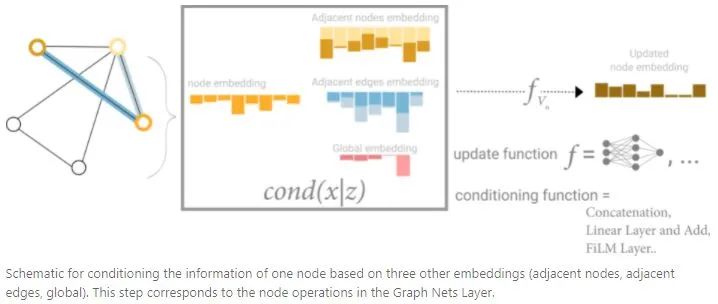
从这个角度看，所有graph属性都可以通过将感兴趣的属性和其他属性关联，然后在pooling过程中利用起来。比如对于一个node，可以同时考虑相邻的node、edge和global信息，然后通过concat将它们关联起来，最后通过线性映射将它们映射到相同特征空间中。

The Challenges of Computation on Graphs

graph在计算中有三个挑战：lack of consistent structure、node-order equivariance和scalability。

Lack of Consistent Structure

graph是极其灵活的数学模型，同时这意味着它们缺乏跨实例的一致结构。比如不同分子之间有不同的结构。用一种可以计算的格式来表示graph并不是一件简单的事情，graph的最终表示通常由实际问题决定。

Node-Order Equivariance

graph的node之间通常没有内在的顺序，相比之下，在图像中，每个像素都是由其在图像中的绝对位置唯一决定的。因此，我们希望我们的算法是节点顺序不变的:它们不应该依赖于graph中node的顺序。如果我们以某种方式对node进行排列，则由算法计算得到的node表示也应该以同样的方式进行排列。

Scalability

graph可以非常大，像Facebook和Twitter这样的社交网络，它们拥有超过10亿的用户，对这么大的数据进行操作并不容易。幸运的是，大多数自然出现的graph都是“稀疏的”:它们的边数往往与顶点数成线性关系。graph的稀疏性导致可以使用特殊的方法有效计算graph中node的表示。另外，和graph的数据量相比，这些方法的参数要少得多。

Problem Setting and Notation

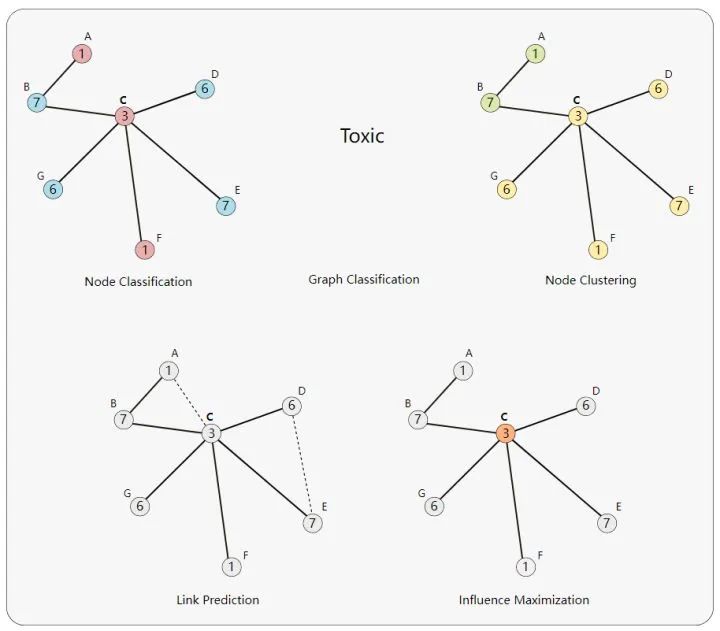
许多问题都可以用graph来表示:

Node Classification: 对单个节点进行分类。

Graph Classification: 对整个图进行分类。

Node Clustering: 根据连接性将相似的节点分组。

Link Prediction: 预测缺失的链接。

Influence Maximization: 识别有影响的节点。

Extending Convolutions to Graphs

卷积神经网络在图像中提取特征方面是非常强大的。而图像本身可以看作是一种非常规则的网格状结构的图，其中单个像素为节点，每个像素处的RGB通道值为节点特征。

因此，将卷积推广到任意的graph是一个很自然的想法。然而，普通卷积不是节点顺序不变的，因为它们依赖于像素的绝对位置。graph可以通过执行某种填充和排序，保证每个节点的邻域结构一致性，但是还有更加普遍和强大的方法来处理这个问题。

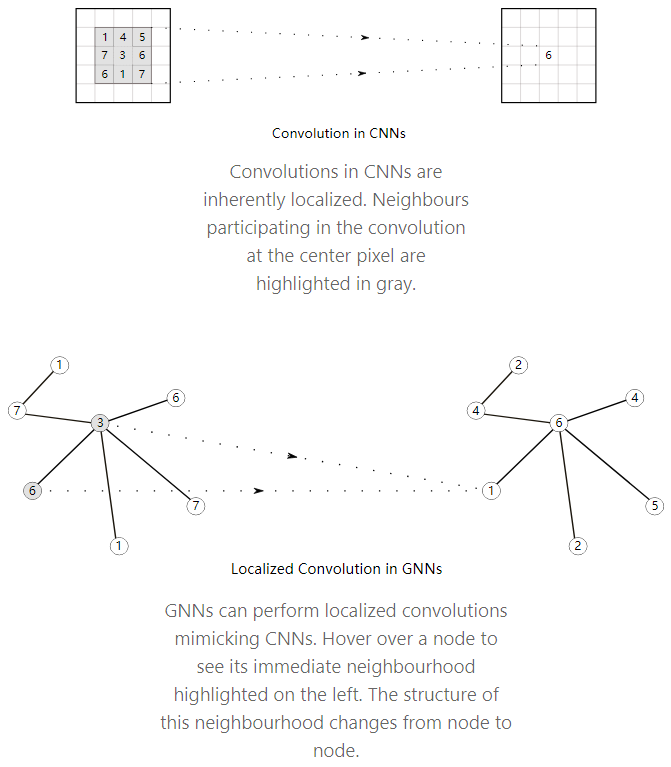
下面首先介绍一下在节点邻域上构造多项式滤波器的方法，这和CNN在相邻像素上滤波类似。然后介绍更多最新的方法如何用更强大的机制扩展这个想法。

Polynomial Filters on Graphs

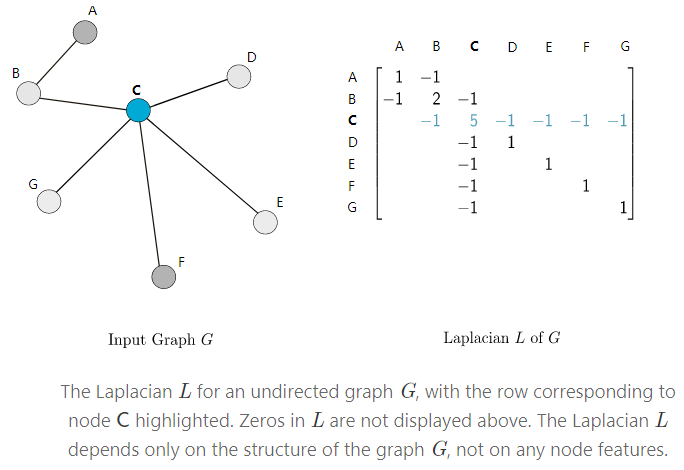
The Graph Laplacian

给定一个graph G，用A来表示数值为0或者1的邻接矩阵，用D表示对角度矩阵(矩阵对角线数值表示与行node相邻node的数量)，那么 $D _ { v } = \sum _ { u } A _ { v u }$ 。graph Laplacian矩阵L可以表示为：L=D - A。右图的对角线就是行node的度数，负数是减去的邻接矩阵(蓝色数字和graph中的C对应)。

Polynomials of the Laplacian

Laplacian的多项式可以表示为：

$p _ { w } ( L ) = w _ { 0 } I _ { n } + w _ { 1 } L + w _ { 2 } L ^ { 2 } + \ldots + w _ { d } L ^ { d } = \sum _ { i = 0 } ^ { d } w _ { i } L ^ { i }$

这些多项式可以认为和CNN中“filters”等价，而系数w是“filters”的权重。

为了方便讨论，下面考虑节点只有一维特性的情况(每个节点是一个数值)。使用前面选择的节点顺序，我们可以将所有节点特征堆在一起得到一个x向量。

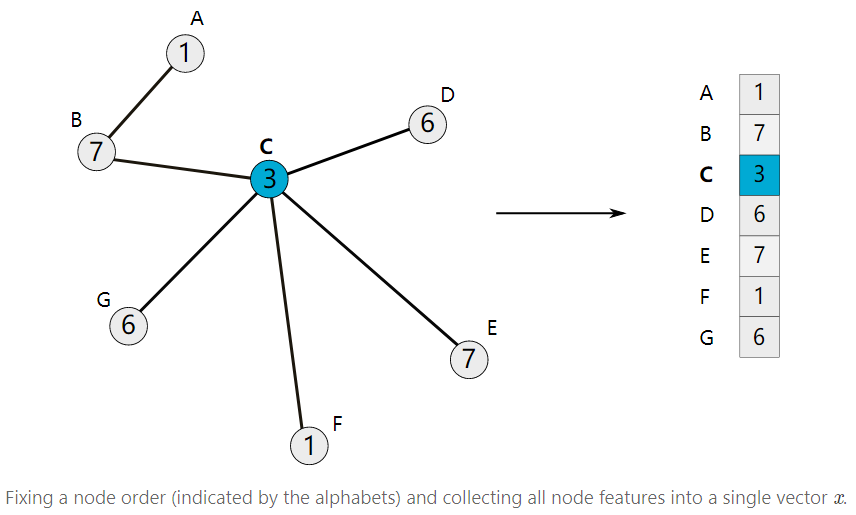
通过构造的特征向量x，可以定义它和多项式滤波器 $p _ { w }$ 的卷积公式为：

$x ^ { \prime } = p _ { w } ( L ) x$

关于Laplacian矩阵如何作用在x上的解释，参照https://distill.pub/2021/understanding-gnns/。

ChebNet

ChebNet对多项式滤波器公式进行了改进:

$p _ { w } ( L ) = \sum _ { i = 1 } ^ { d } w _ { i } T _ { i } ( \tilde { L } )$

其中 $T_{i}$ 是度数为i的第一种切比雪夫多项式， $\tilde { L }$ 是使用L最大特征值定义的归一化Laplacian矩阵。关于ChebNet细节参照https://distill.pub/2021/understanding-gnns/。

Embedding Computation

下面介绍一下如何堆叠带非线性的ChebNet(或者任何多项式过滤器) layer构建成一个GNN，就像标准的CNN一样。假设有K个不同的多项式过滤器层， $k ^ { \text {th } }$ 的可学习参数表示为 $w ^ { ( k ) }$ ，那么计算过程可以表示成：

GNN和CNN计算方式类似，将输入作为初始features，然后计算多项式过滤器，然后和输入特征进行矩阵相乘，最后用非线性函数进行非线性变换，循环迭代K次。

需要注意的是，GNN在不同的节点上过滤器权重参数共享，和CNN类似，CNN的卷积在不同位置也是参数共享的。

Modern Graph Neural Networks

ChebNet是graph中学习局部过滤器的一个突破，它激发了许多人从不同的角度思考图卷积。

多项式过滤器对x卷积可以展开为：

$\begin{aligned} ( L x ) _ { v } & = L _ { v } x \\ & = \sum _ { u \in G } L _ { v u } x _ { u } \\ & = \sum _ { u \in G } \left( D _ { v u } - A _ { v u } \right) x _ { u } \\ & = D _ { v } x _ { v } - \sum _ { u \in \mathcal { N } ( v ) } x _ { u } \end{aligned}$

这其实是一个1步局部卷积(也就是只跟直接相连的node卷积)，可以看成由两个步骤产生：

1.聚合直接相邻的特征 $x_{u}$ 。

2.结合node自身的特征 $x_{v}$ 。

通过确保聚合是node-order equivariant，来保证整个卷积是node-order equivariant。

这些卷积可以被认为是相邻节点之间的“message passing”:在每一步之后，每个节点从它的相邻节点接收信息。

通过迭代重复K次1步局部卷积，感受野为K步远的所有node。

Embedding Computation

Message-passing形成了很多GNN模型的backbone。下面介绍一些流行的GNN模型:

Graph Convolutional Networks (GCN)
Graph Attention Networks (GAT)
Graph Sample and Aggregate (GraphSAGE)
Graph Isomorphism Network (GIN)

GCN

GAT

GraphSAGE

GIN

比较一下GCN、GAT、GraphSAGE和GIN的形式，主要差别就在于如何聚合信息和如何传递信息。

Conclusion

本文只是简单介绍了一下GNN和GCN的一些变体，但图神经网络的领域是极其广阔的。下面提一下一些可能感兴趣的点：

GNNs in Practice：如何提高GNN的效率、GNN的正则化技术

Different Kinds of Graphs：Directed graphs、Temporal graphs、Heterogeneous graphs

Pooling：SortPool、DiffPool、SAGPool

往期精彩回顾




适合初学者入门人工智能的路线及资料下载
机器学习及深度学习笔记等资料打印
机器学习在线手册
深度学习笔记专辑
《统计学习方法》的代码复现专辑
AI基础下载
黄海广老师《机器学习课程》视频课
黄海广老师《机器学习课程》711页完整版课件
本站qq群554839127，加入微信群请扫码：