CNN卷积神经网络入门超详细解析-技术圈

点击下方卡片，关注“新机器视觉”公众号

视觉/图像重磅干货，第一时间送达

来源：CSDN

作者：越前浩波

一、神经网络

首先了解什么是神经网络，大家可以先看下以下两篇博客，一篇为纯理论讲解，一篇为实战加理论，在此就不过多详细介绍。

机器学习之神经网络学习及其模型（https://blog.csdn.net/weixin_44023658/article/details/105691321）
入门讲解：使用numpy实现简单的神经网络（BP算法）
（https://blog.csdn.net/weixin_44023658/article/details/105694079）

二、卷积神经网络之层级结构

要了解卷积神经网络首先要了解它的各个层级结构，如下图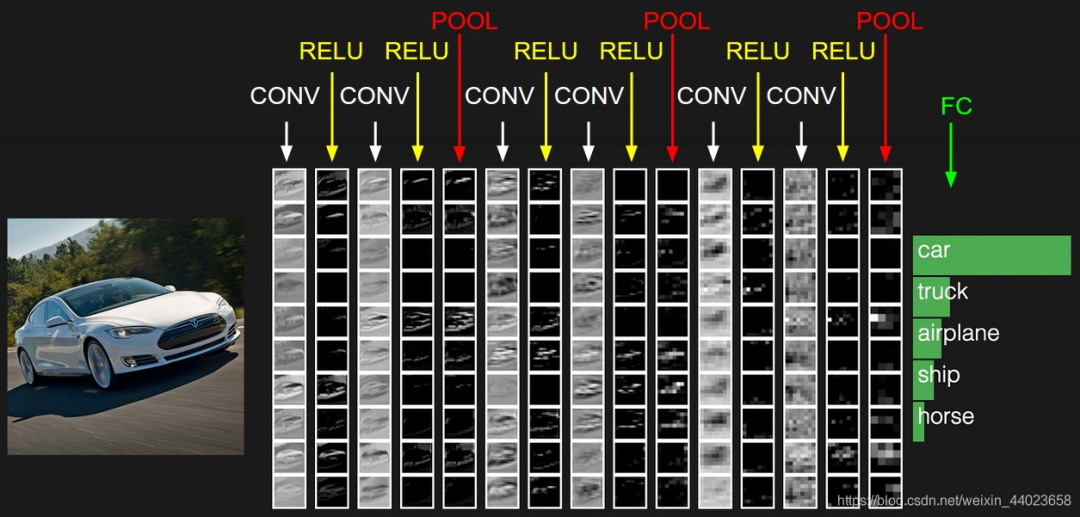
上图中CNN要做的事情是：给定一张图片，是车还是马未知，是什么车也未知，现在需要模型判断这张图片里具体是一个什么东西，总之输出一个结果：如果是车那是什么车
所以

上图从左到右依次为→

数据输入层：对数据做一些处理，比如去均值（把输入数据各个维度都中心化为0，避免数据过多偏差，影响训练效果）、归一化（把所有的数据都归一到同样的范围）、PCA/白化等等。CNN只对训练集做“去均值”这一步。
CONV：卷积计算层，线性乘积求和。
RELU：激励层，上文2.2节中有提到：ReLU是激活函数的一种
POOL：池化层，简言之，即取区域平均或最大
FC：全连接层

这几个部分中，卷积计算层是CNN的核心，下文将重点阐述此部分。

三、CNN之卷积计算层

1、 CNN如何进行识别
简言之，当我们给定一个"X"的图案，计算机如何识别这个图案就是“X”呢？一个可能的办法就是计算机存储一张标准的“X”图案，然后把需要识别的未知图案跟标准"X"图案进行比对，如果二者一致，则判定未知图案即是一个"X"图案。

这样即便未知图案可能有一些平移或稍稍变形，依然能辨别出它是一个X图案。所以，CNN是把未知图案和标准X图案一个局部一个局部的对比，如下图所示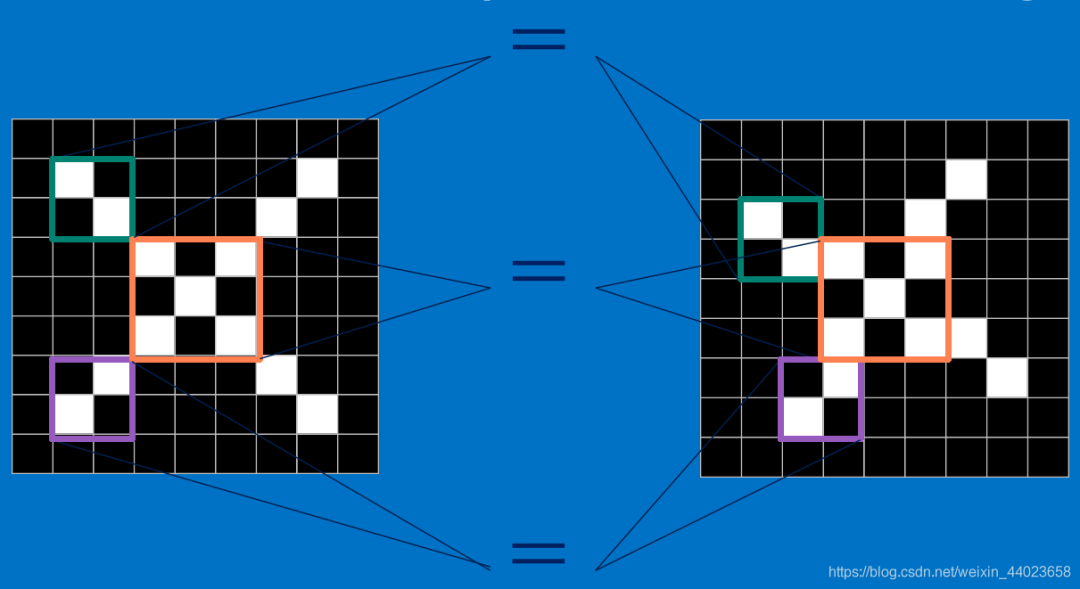
而未知图案的局部和标准X图案的局部一个一个比对时的计算过程，便是卷积操作。卷积计算结果为1表示匹配，否则不匹配。

具体来说，为了确定一幅图像是包含有"X"还是"O"，我们需要判断它是否含有"X"或者"O"，并且假设必须两者选其一，不是"X"就是"O"。
理想的情况如下图所示：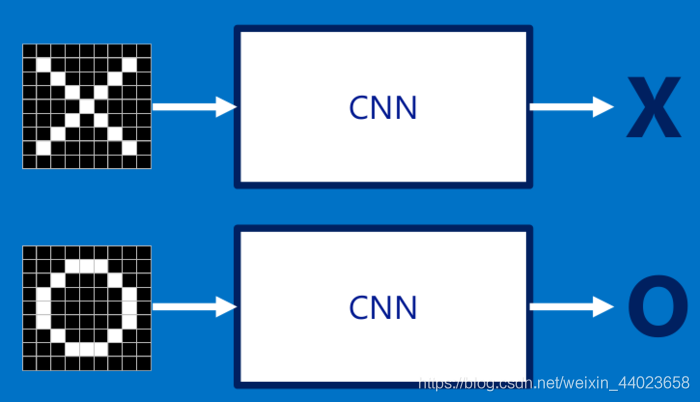
标准的"X"和"O"，字母位于图像的正中央，并且比例合适，无变形

对于计算机来说，只要图像稍稍有一点变化，不是标准的，那在识别过程中就会遇到困难：
计算机要解决上面这个问题，一个比较直接的做法就是先保存一张"X"和"O"的标准图像（就像前面给出的例子），然后将其他的新给出的图像来和这两张标准图像进行对比，看看到底和哪一张图更匹配，就判断为哪个字母。

但是这么做的话，精准度较低，因为在在计算机的“视觉”中，一幅图看起来就像是一个二维的像素数组（可以想象成一个棋盘），每一个位置对应一个数字。在我们这个例子当中，像素值"1"代表白色，像素值"-1"代表黑色。
当比较两幅图的时候，如果有任何一个像素值不匹配，那么这两幅图就不匹配，至少对于计算机来说是这样的。

所以，上述事例中，计算机认为两幅图中的白色像素除了中间的3*3的小方格里面是相同的，其他四个角上都不同：

从表面上看，计算机会判别右边那幅图不是"X"，两幅图不同，则得出结论：
但是这么做，显得太不合理，理想的状况下，我们希望对于那些仅仅只是做了一些像平移，缩放，旋转，微变形等简单变换的图像，计算机仍然能够识别出图中的"X"和"O"。

如下图所示，我们希望计算机依然能够很快并且很准的识别出图像：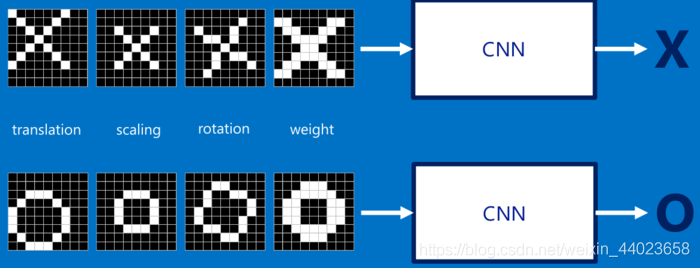
于是就有了CNN。

2、特征提取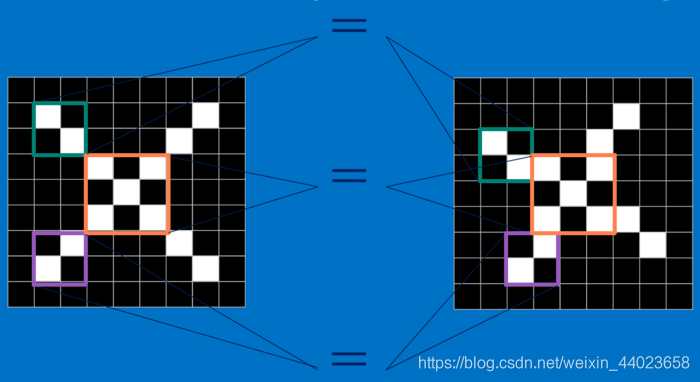不同于计算机，对于CNN来说，是通过一块一块地来进行比对，比对的这个“小块”我们称之为Features（特征）。在两幅图中大致相同的位置找到一些粗糙的特征进行匹配，相比传统的整幅图逐一比对的方法，CNN能够更好的看到两幅图的相似性。

每一个feature就像是一个小图（就是一个比较小的有值的二维数组）。不同的Feature匹配图像中不同的特征。在字母"X"的例子中，那些由对角线和交叉线组成的features基本上能够识别出大多数"X"所具有的重要特征。
这些features很有可能就是匹配任何含有字母"X"的图中字母X的四个角和它的中心。那么具体到底是怎么匹配的呢？如下所示：

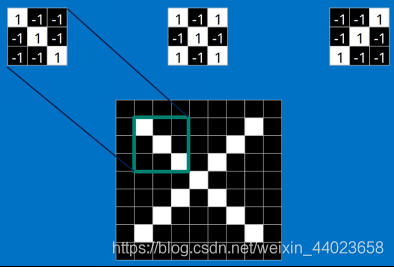
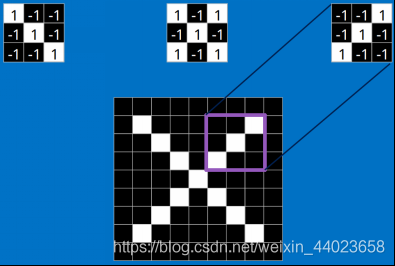
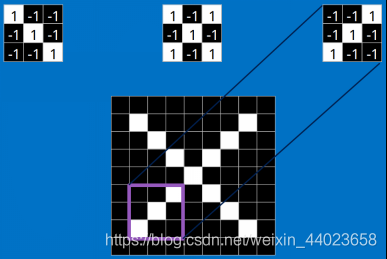
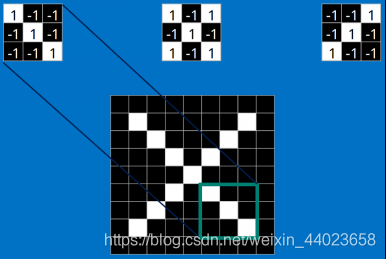
看到这里是不是已经有了一些头绪，但其实目前只是第一步，现在知道了这些Features是怎么在原图上面进行匹配的，但是还不知道如何通过Features进行数学计算，比如这个下面3*3的小块到底如何计算的。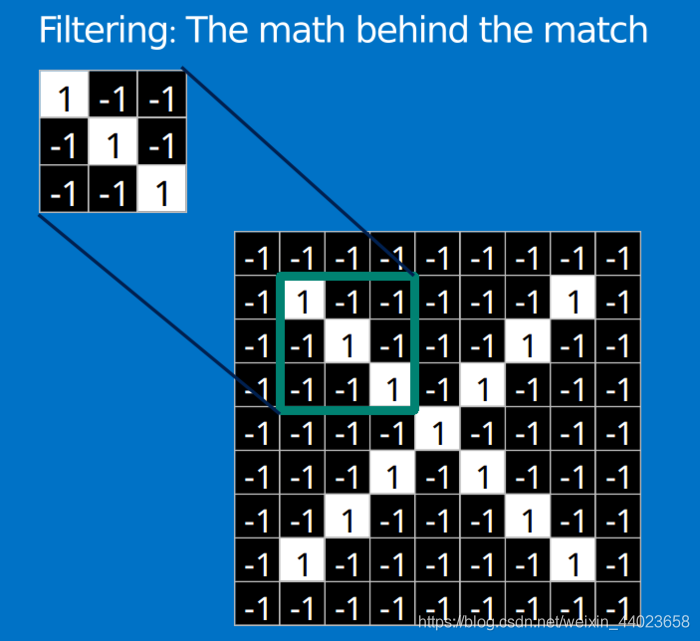这里面的数学操作，就是我们常说的“卷积”操作。

下面会介绍卷积操作的详细步骤。

2、什么是卷积
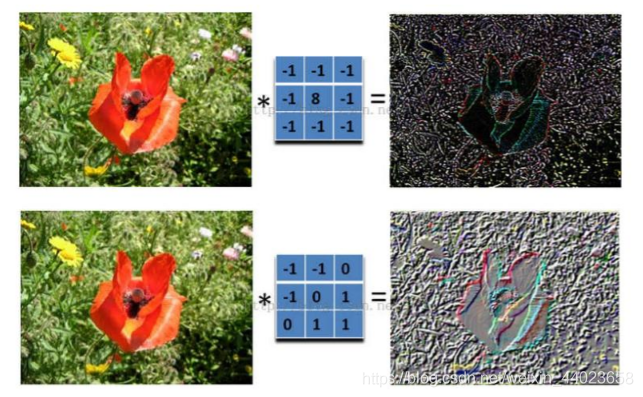
对图像（不同的数据窗口数据）和滤波矩阵（一组固定的权重：因为每个神经元的多个权重固定，所以又可以看做一个恒定的滤波器filter）做内积（逐个元素相乘再求和）的操作就是所谓的『卷积』操作，也是卷积神经网络的名字来源。

非严格意义上来讲，下图中红框框起来的部分便可以理解为一个滤波器，即带着一组固定权重的神经元。多个滤波器叠加成了卷积层。

举个具体的例子，比如下图中，图中左边部分是原始输入数据，图中中间部分是滤波器filter，图中右边是输出的新的二维数据。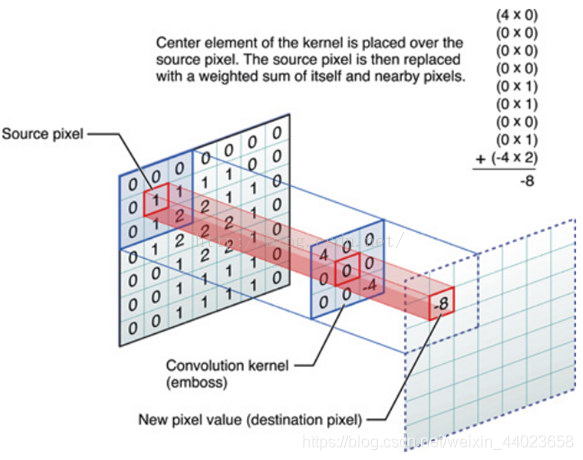
中间滤波器filter与数据窗口做内积，其具体计算过程则是：40 + 00 + 00 + 00 + 01 + 01 + 00 + 01 + -4*2 = -8

3、图像上的卷积

在下图对应的计算过程中，输入是一定区域大小(width*height)的数据，和滤波器filter（带着一组固定权重的神经元）做内积后等到新的二维数据。

左边是图像输入，中间部分就是滤波器filter（带着一组固定权重的神经元），不同的滤波器filter会得到不同的输出数据，比如颜色深浅、轮廓。相当于如果想提取图像的不同特征，则用不同的滤波器filter，提取想要的关于图像的特定信息：颜色深浅或轮廓。

如下图所示：

4、动态卷积图演示
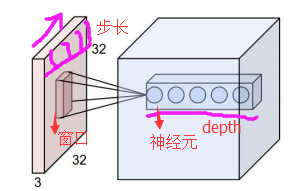
在CNN中，滤波器filter（带着一组固定权重的神经元）对局部输入数据进行卷积计算。每计算完一个数据窗口内的局部数据后，数据窗口不断平移滑动，直到计算完所有数据。这个过程中，有这么几个参数：

a. 深度depth：神经元个数，决定输出的depth厚度。同时代表滤波器个数。
b. 步长stride：决定滑动多少步可以到边缘。
c.填充值zero-padding：在外围边缘补充若干圈0，方便从初始位置以步长为单位可以刚好滑倒末尾位置，通俗地讲就是为了总长能被步长整除。

cs231n课程中有一张卷积动图，如下图所示：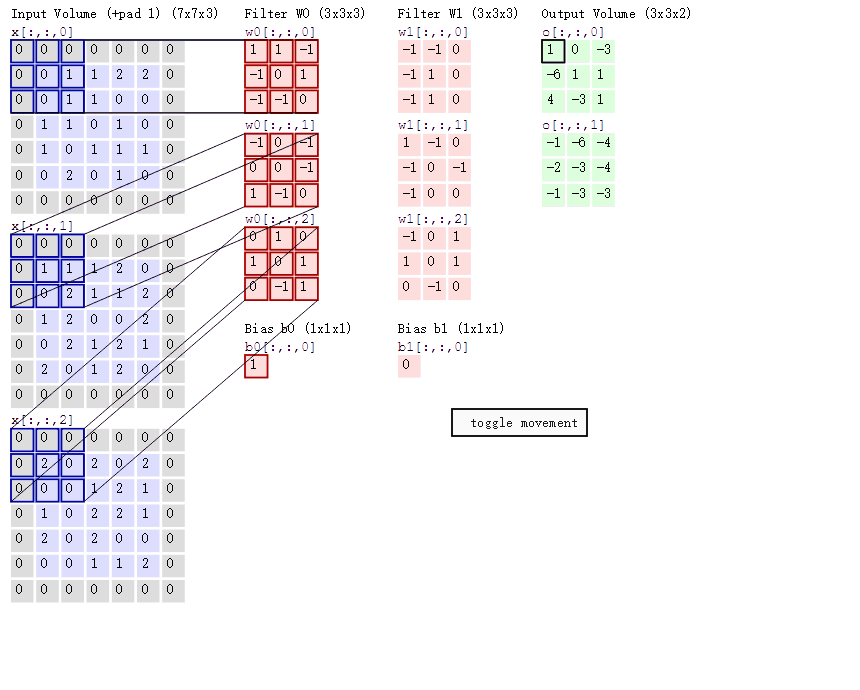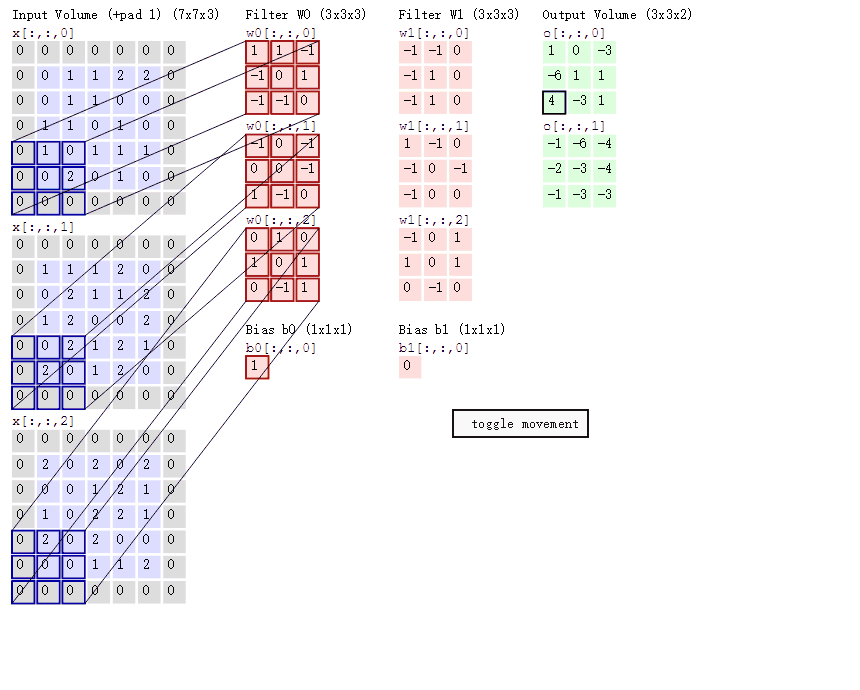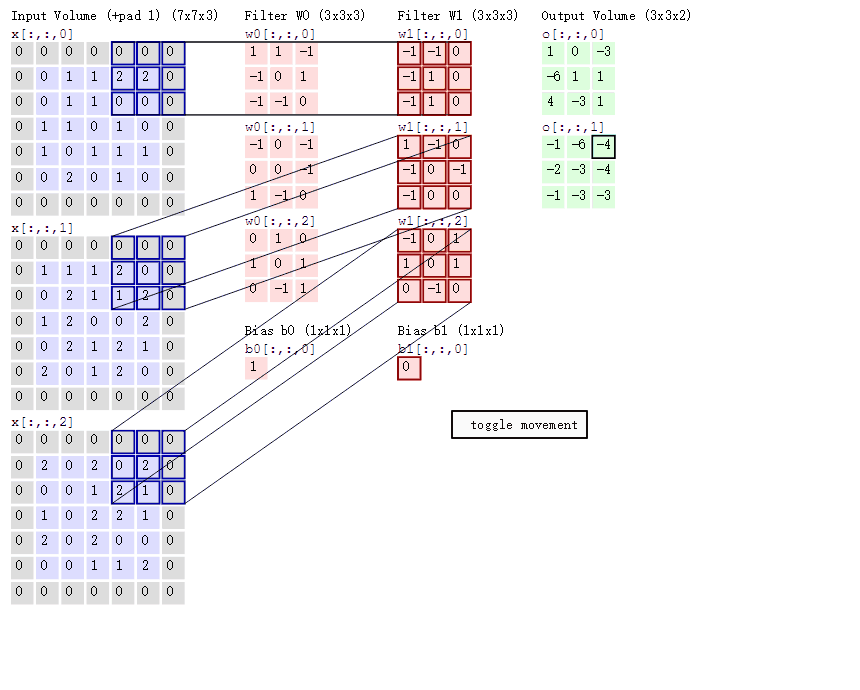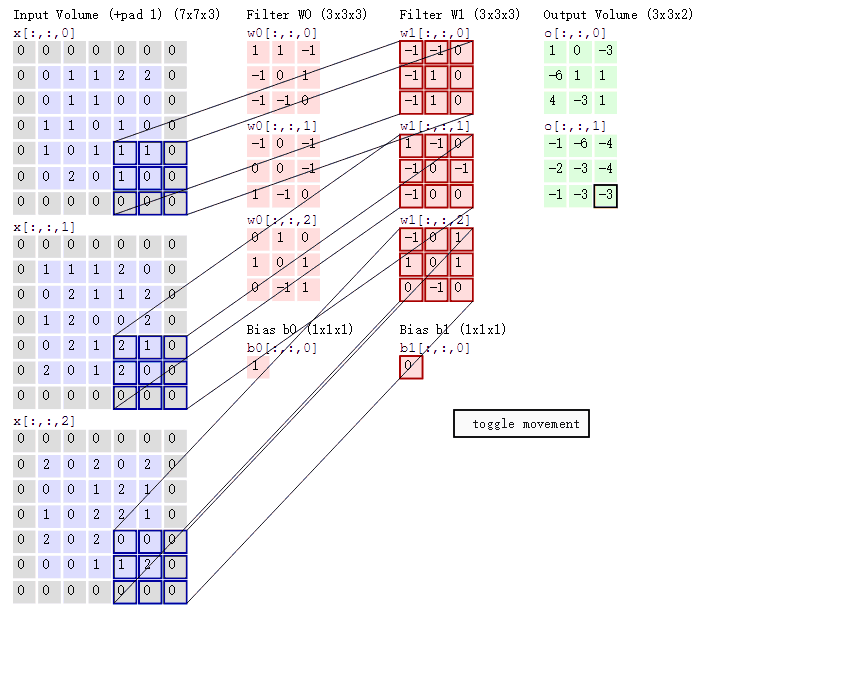
通过上图我们可以看到：

两个神经元，即depth=2，意味着有两个滤波器。数据窗口每次移动两个步长取3*3的局部数据，即stride=2；zero-padding=1，然后分别以两个滤波器filter为轴滑动数组进行卷积计算，得到两组不同的结果。

如果初看上图，可能不一定能马上理解，但结合上文的内容后，便可以更清晰的理解其含义。

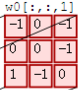
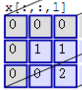
左边是输入（773中，7*7代表图像的像素/长宽，3代表R、G、B 三个颜色通道），中间部分是两个不同的滤波器Filter w0、Filter w1，最右边则是两个不同的输出。

随着左边数据窗口的平移滑动，滤波器Filter w0 / Filter w1对不同的局部数据进行卷积计算。值得一提的是，左边数据在变化，每次滤波器都是针对某一局部的数据窗口进行卷积，这就是所谓的CNN中的局部感知机制。

举个例子，滤波器就像一双眼睛，人类视角有限，一眼望去，只能看到这世界的局部。如果一下子接受全世界所有信息，大脑会接收不过来。当然，即便是看局部，针对局部里的信息人类双眼也是有偏重、偏好的，会根据自己的兴趣爱好进行输入的权重的分配。

与此同时，数据窗口滑动，导致输入在变化，但中间滤波器Filter w0的权重（即每个神经元连接数据窗口的权重）是固定不变的，这个权重不变即所谓的CNN中的参数（权重）共享机制。

再举个例子，某人环游全世界，所看到的信息在变，但采集信息的双眼不变，另外不同人的双眼看同一个局部信息
所感受到的不同，即一千个读者有一千个哈姆雷特，所以不同的滤波器就像不同的双眼，不同的人有着不同的反馈结果。

我第一次看到上面这个动态图的时候，只觉得很炫，另外就是只初步了解计算过程是“相乘后相加”，但到底具体是个怎么相乘后相加的计算过程变不得而知，后续通过学习后才有了更深入的了解。

下面我们就来详细说明下其计算步骤。

首先，我们将上述动图进行分解，如下图
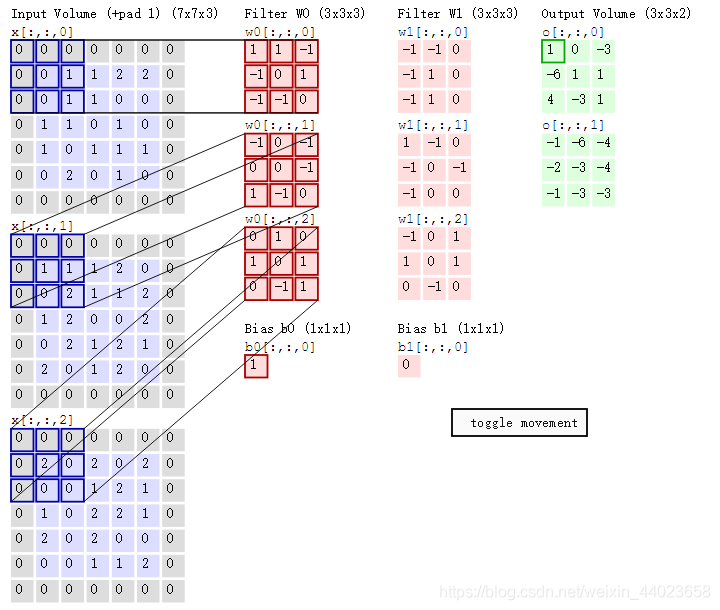
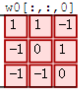
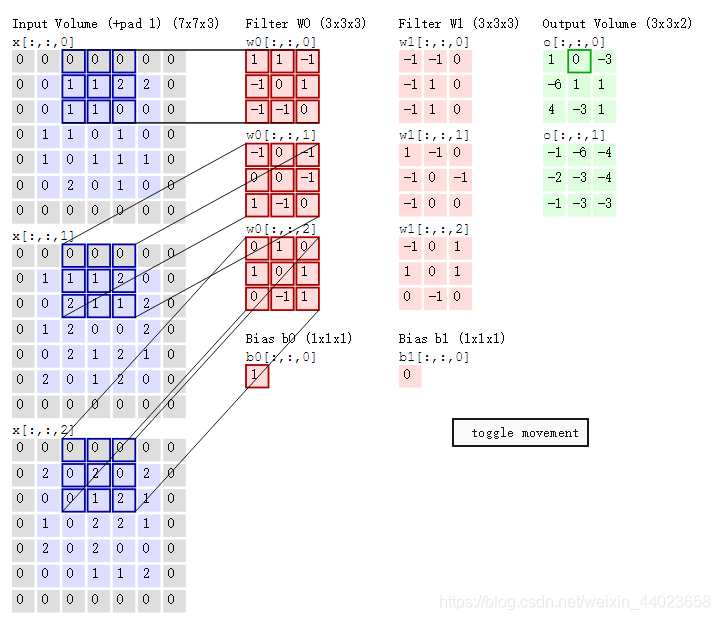
其次，我们细究下上图的具体计算过程。即上图中的输出结果1具体是怎么计算得到，其原理类似wx + b，w对应滤波器Filter w0，x对应不同的数据窗口，b对应Bias b0，相当于滤波器Filter w0与一个个数据窗口相乘再求和后，最后加上Bias b0得到输出结果1，具体过程如下过程所示：

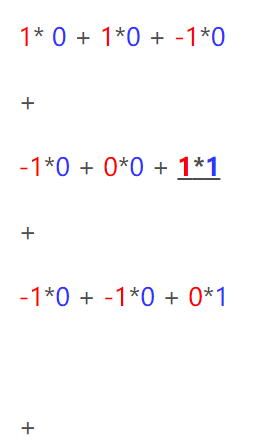
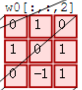
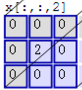
然后滤波器Filter w0固定不变，数据窗口向右移动2步，继续做内积计算，得到0的输出结果
最后，换做另外一个不同的滤波器Filter w1、不同的偏置Bias b1，再跟图中最左边的数据窗口做卷积，可得到另外一个不同的输出。

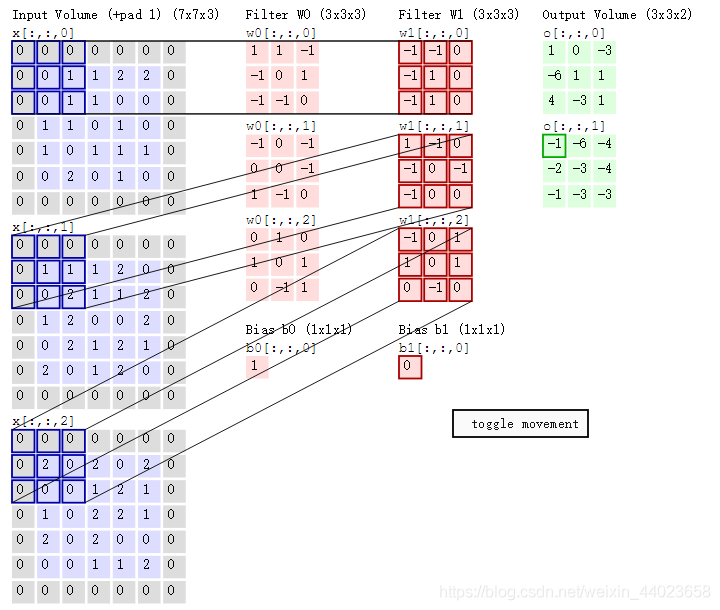
以上就是CNN在图像上进行的卷积的整个计算过程。

四、 CNN之激励层，池化层，全连接层

1、 ReLU激励层
第一节俩篇博客介绍了激活函数sigmoid，但实际梯度下降中，sigmoid容易饱和、造成终止梯度传递，且没有0中心化。咋办呢，可以尝试另外一个激活函数：ReLU，其图形表示如下图所示：

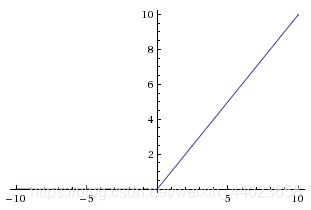
对于输入的负值，输出全为0，对于正值，原样输出。

下图演示了本文的例子中relu激活函数具体操作：

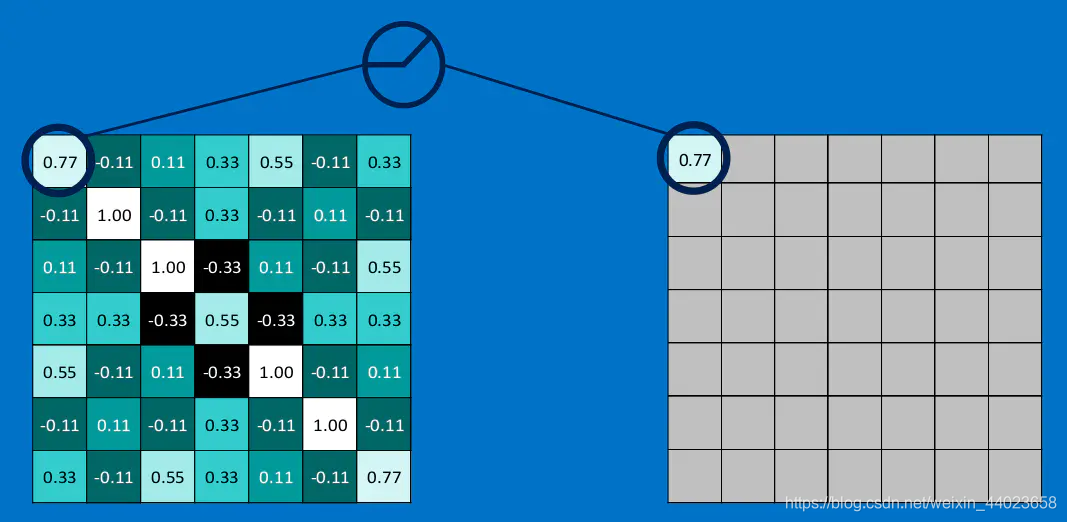
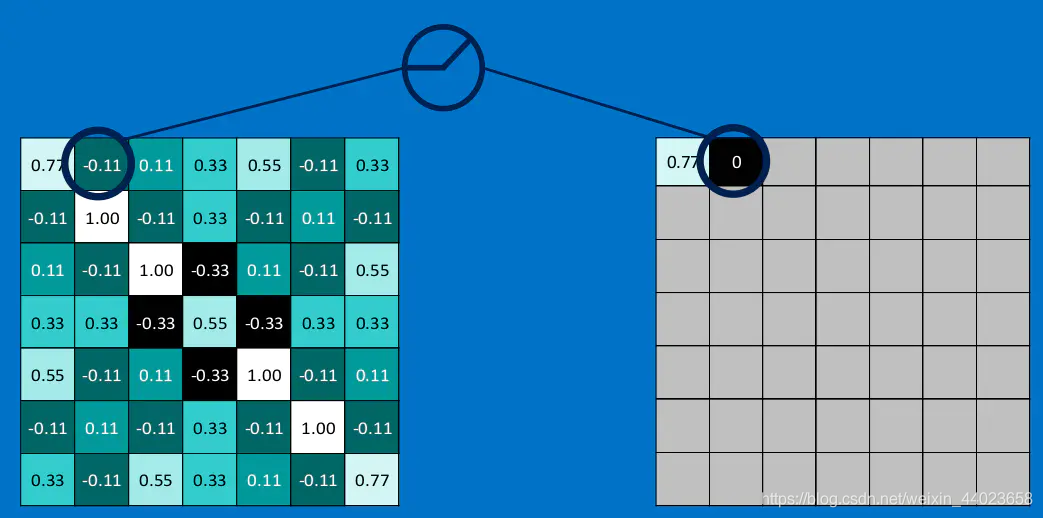
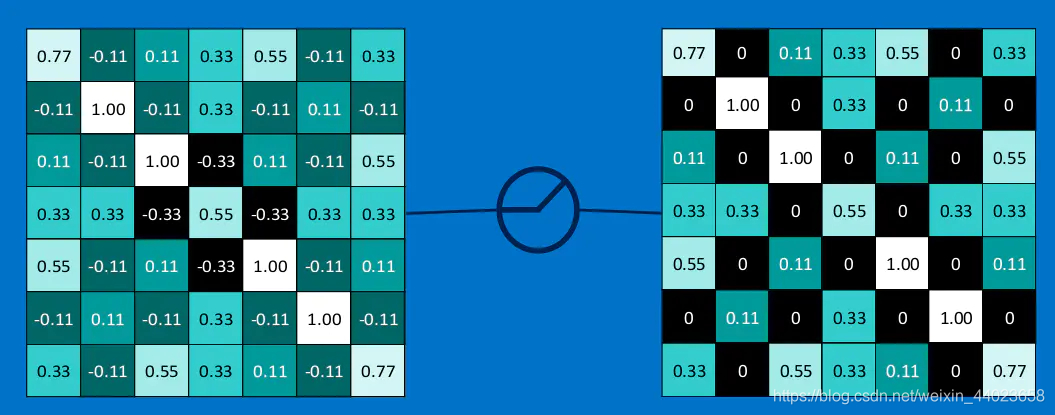
我们将上面所提到的卷积，池化，激活放在一起，于是形成下面这个样子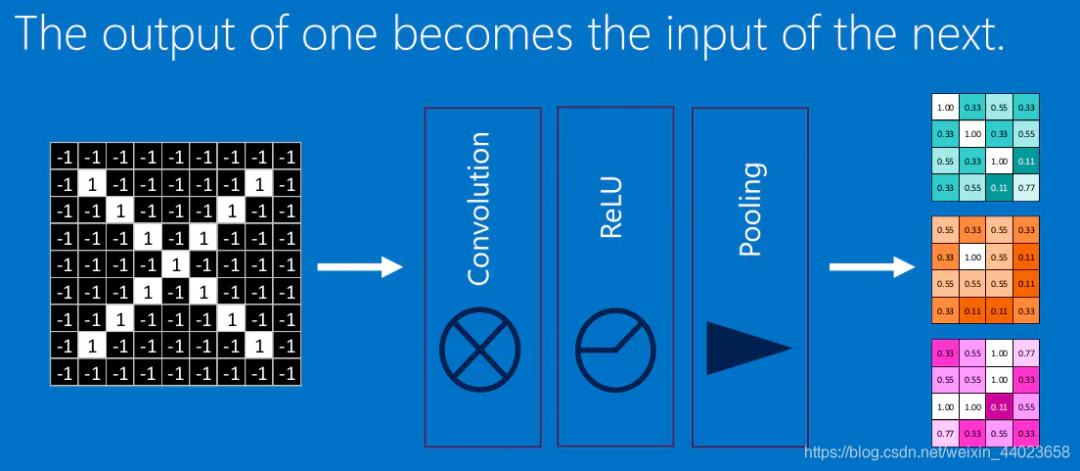：然后，我们加大网络的深度，增加更多的层，就可以得到深度神经网络了：

2、池化pool层
前面提到，池化，简言之，即取区域平均或最大，如下图所示，CNN中使用的另一个有效的工具被称为“池化(Pooling)”。池化可以将一幅大的图像缩小，同时又保留其中的重要信息。池化就是将输入图像进行缩小，减少像素信息，只保留重要信息。通常情况下，池化都是22大小，比如对于max-pooling来说，就是取输入图像中22大小的块中的最大值，作为结果的像素值，相当于将原始图像缩小了4倍。(注：同理，对于average-pooling来说，就是取2*2大小块的平均值作为结果的像素值。)

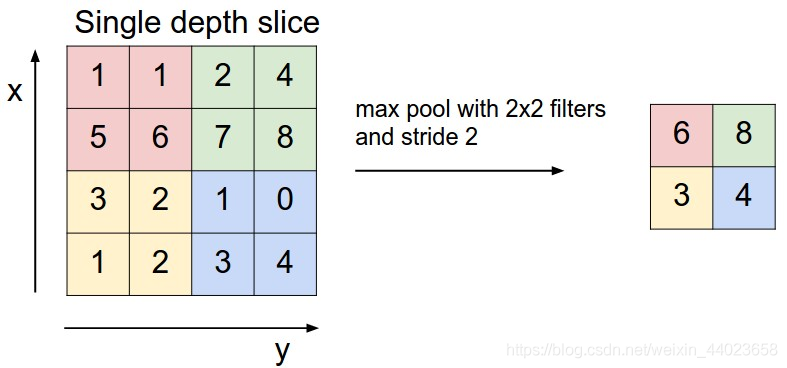上图所展示的是取区域最大，即上图左边部分中左上角2x2的矩阵中6最大，右上角2x2的矩阵中8最大，左下角2x2的矩阵中3最大，右下角2x2的矩阵中4最大，所以得到上图右边部分的结果：6 8 3 4。