图卷积网络-图的深度学习
作者 | Francesco Casalegno
作者 | Francesco Casalegno
编译 | VK
来源 | Towards Data Science

为什么是图
Traffic patterns forecasting on road networks (https://arxiv.org/abs/1802.07007) Inferring missing information in a Knowledge Graph (https://arxiv.org/abs/1706.05674) Predicting protein interactions for drug discovery (https://papers.nips.cc/paper/2017/file/f507783927f2ec2737ba40afbd17efb5-Paper.pdf) Recommender systems based on social networks data (https://arxiv.org/abs/1902.07243)
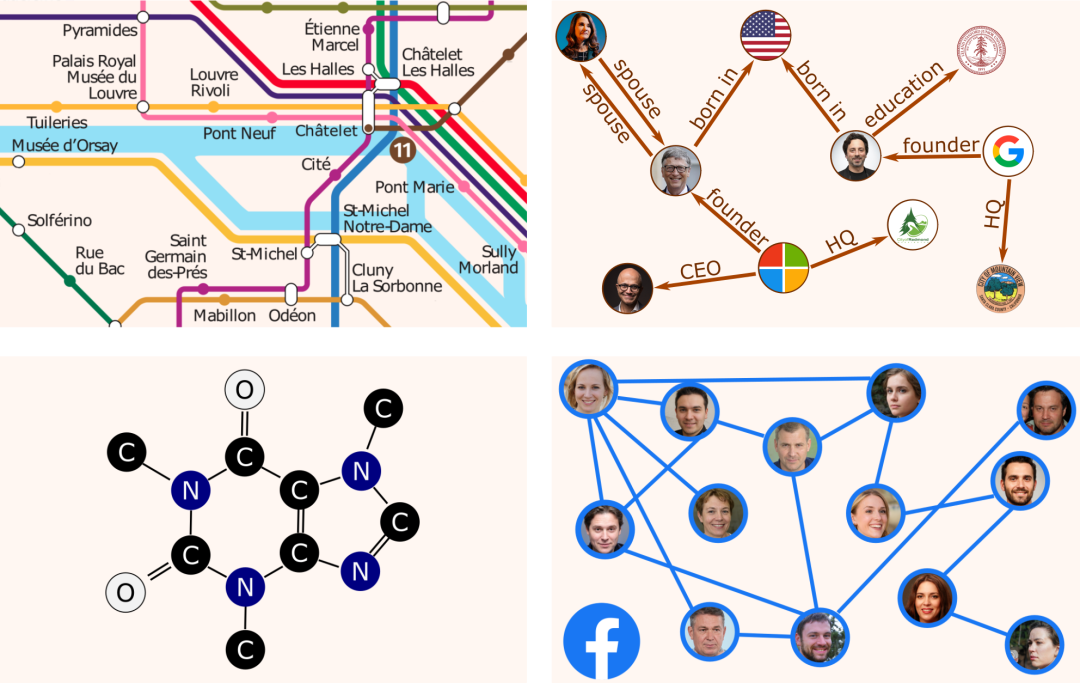
Traffic patterns forecasting on road networks (https://arxiv.org/abs/1802.07007) Inferring missing information in a Knowledge Graph (https://arxiv.org/abs/1706.05674) Predicting protein interactions for drug discovery (https://papers.nips.cc/paper/2017/file/f507783927f2ec2737ba40afbd17efb5-Paper.pdf) Recommender systems based on social networks data (https://arxiv.org/abs/1902.07243)
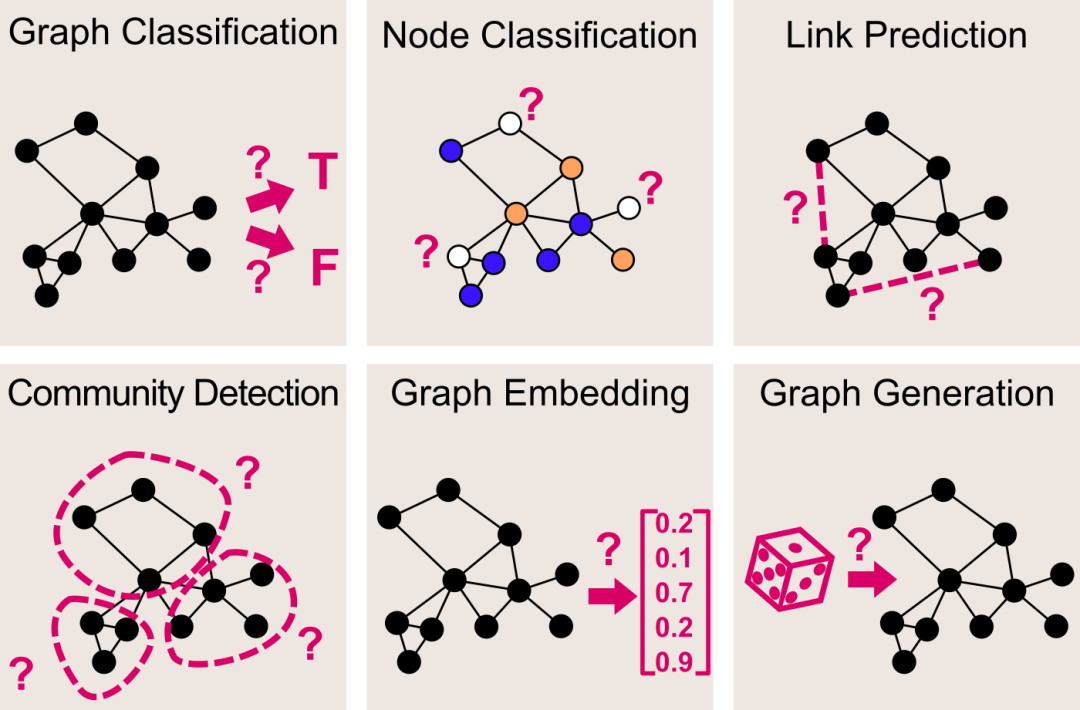
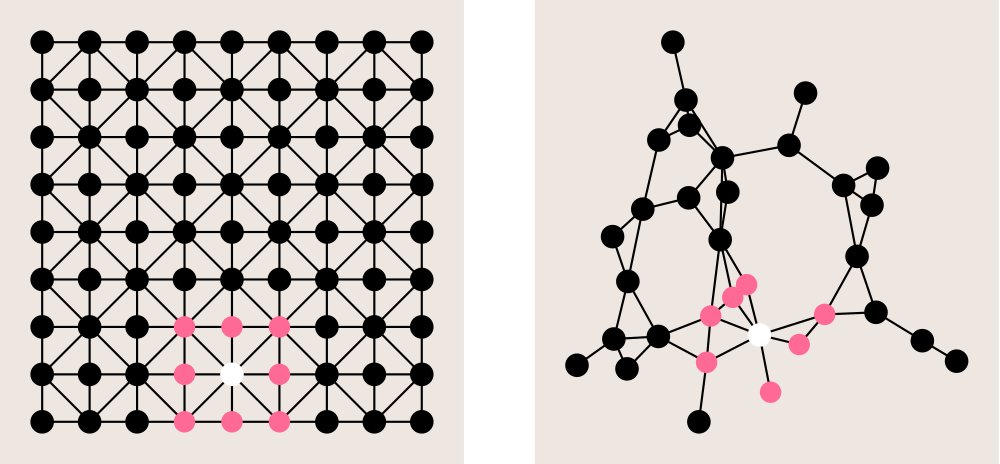
为什么是卷积
在1D中,处理音频信号-例如用于声音分类 在2D中,处理图像-例如用于早期龋齿检测 在3D技术中,处理扫描,例如核磁共振脑成像
定义图卷积
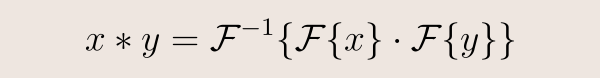
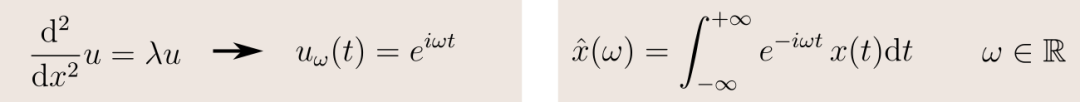

D、 度矩阵是对角线矩阵,包含每个顶点的边数; A、 邻接矩阵表示每对顶点是否通过边连接。



全神经网络的建立
通过一系列的局部卷积滤波器和池化层来提取HxWxC输入图像的特征。 产生的特征通道被映射到一个固定大小的向量,例如使用一个全局池层。 最后,使用几个全连接的层来产生最终的分类输出。
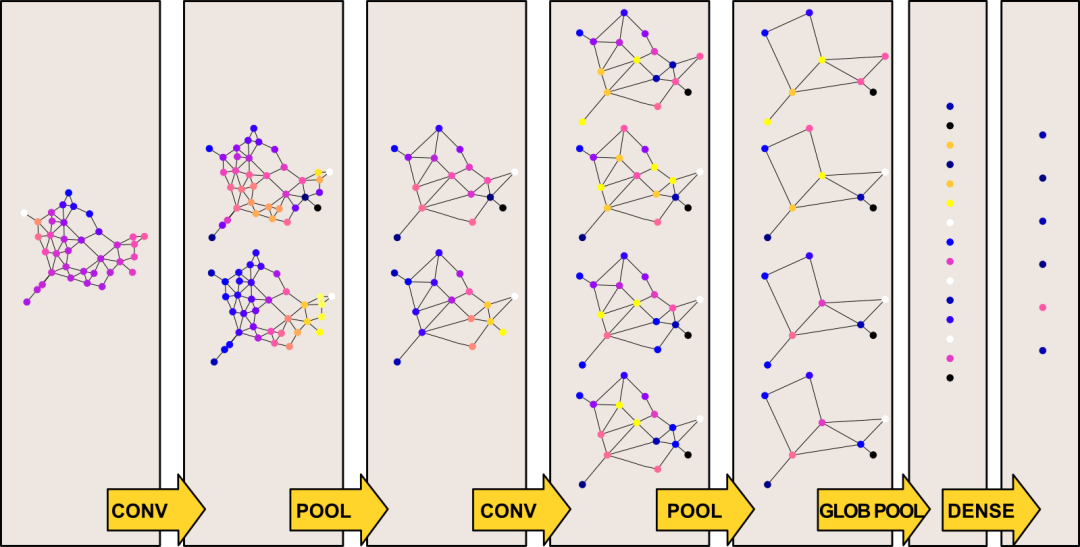
NxC向量x,对于图的N个节点中的每一个顶点,包含C个特征 NxN邻接矩阵
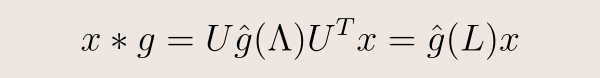
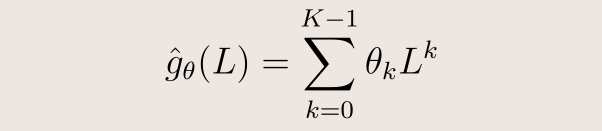
结论
从知识图到社交网络,图应用无处不在。 卷积神经网络(CNNs)在许多领域都取得了成功,可以推广到图卷积网络(GCNs)。 图的卷积是通过图的傅立叶变换来定义的。 图傅里叶变换又被定义为拉普拉斯特征值的投影。 对于传统的cnn,GCN由几个卷积层和池层组成,用于特征提取,然后是最后的完全连接层。 为了确保卷积滤波器具有紧凑的支持,我们使用多项式参数化。切比雪夫多项式可以降低计算复杂度。
往期精彩回顾
本站qq群851320808,加入微信群请扫码:
评论
