图卷积网络GCN的详尽介绍
共 7960字，需浏览 16分钟
·
2022-06-08 20:09
转载来源：Nango明楠（授权原创声明）https://zhuanlan.zhihu.com/p/90470499
1.背景
图卷积的核心思想是利用『边的信息』对『节点信息』进行『聚合』从而生成新的『节点表示』, 有的研究在此基础上利用『节点表示』生成『边表示』或是『图表示』完成自己的任务.
卷积网络的卷积, 本质是通过滤波器来对某个空间区域的像素点进行加权求和,得到新的特征表示的过程. 加权系数就是卷积核的参数，如图所示：
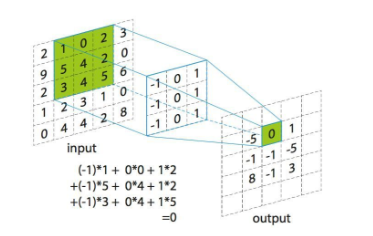
CNN适用于规则二维矩阵数据 (如图1, 每个像素点有上下左右相连), 或一维序列数据(如语音,每个点左右相连) 来提取特征.
然而很多数据类型不具备规则的结构(称为非欧几里得数据,Non Euclidean Structure Data),如社交网络, 推荐系统上抽取的图谱, 每个节点可能有不一样连接方式. 图卷积中的graph 指的也就是 图论中用顶点和边建立相关关系的拓扑图，如图2所示“非欧几里得结构的数据示例”
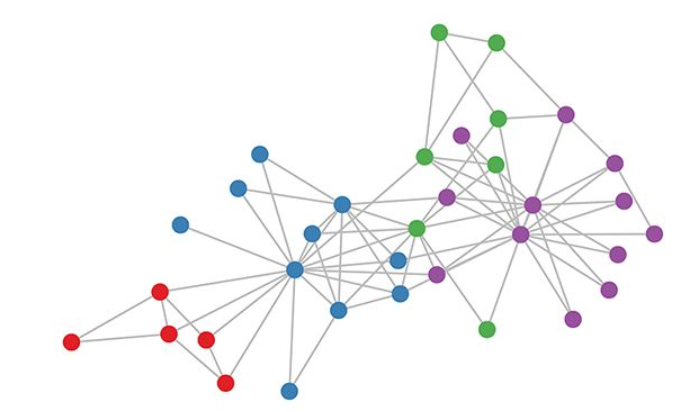
CNN无法处理非欧几里得结构的数据, 因为传统的卷积没法处理节点关系多变的信息(没法固定尺寸进行设置卷积核 及其他问题), 为了从这样的数据结构有效地提取特征, GCN成为研究热点.
广义上来说, 任何数据在在赋范空间内都可以建立拓扑关联. 简单地说, 二维图像也可以构成拓扑图. 如下简单例子.
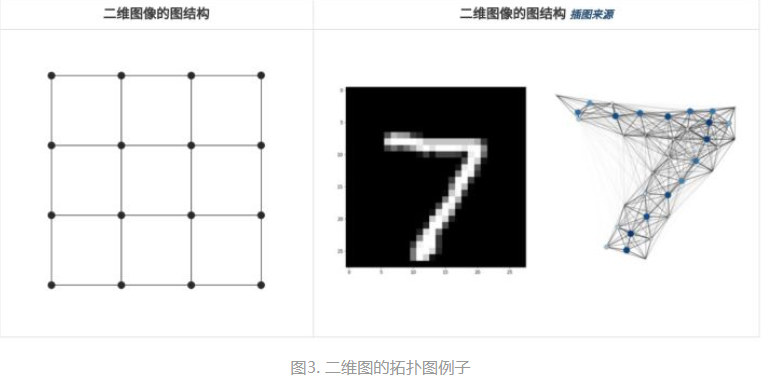
图数据的特点是:
1. 节点特征: 每个节点都具有自己的向量表示; 2. 结构特征: 节点与节点间具有一定的联系, 即携带信息的边.
GCN的目的就是用来提取拓扑图的空间特征。
而GCN主要有两类解释方法，一是基于顶点域或空间域 vertex domain(spatial domain)，另一种则是基于频域或谱域spectral domain 。即顶点域可以类比到直接在图片的像素点上进行卷积，而频域可以类比到对图片进行傅里叶变换后，再进行卷积。两类其实就是从两个不同的角度理解，空间的角度理解会简单些, 而谱方法的推导和思路是比较严谨和理论的方法
2.顶点域来解释GCN
先从简单的顶点域角度说起. 定义几个符号:
表示所有节点的编号。 表示所有节点的特征，表示节点的特征。 表示邻接矩阵，表示节点和节点之间之间边的权重(目前没有自环,即)。
每个节点, 收集来自邻居传递的信息, 然后汇总后更新自己.
2.1平均法
最简单的是平均法, 物以类聚, 每个节点和它邻居都是相似的, 那么每个节点就等于邻居节点的平均值。
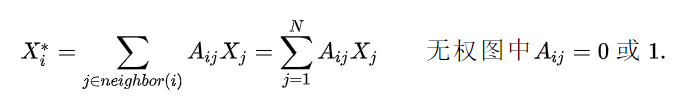
所以对于所有节点, 其平均法的更新过程为(写成矩阵运算):
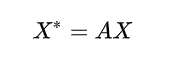
2.2 加权平均法
每个节点和邻居的关系强度是不同的, 考虑到边的权重关系, 只需要将邻接矩阵变为有权图, 即让 的取值不局限于{0,1}, 而是任何合适的权值. (有些工作研究如何构建有权图, 简单的如利用高斯分布赋权值).
对所有节点的加权平均,更新过程为:
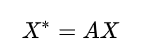
2.3 GCN的简单例子
对汇聚节点, 加入线性变换矩阵 , 将该节点的汇聚特征 变换到 h 维度空间( 为激活函数) :
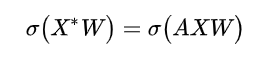
故节点特征在GCN的前后变化为:
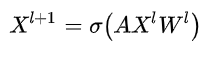
上式是最基础的表达方式, 通过叠加GCN就可以得到节点的维的特征, 其中维度 是自定义的超参, 一般GCN最后一层的特征维度 和某固定维度对齐(如属性或视觉特征的维度数).
比如我们叠加两层GCN, 每个节点可以把 2-hops 邻居的特征加以聚合,得到自身特征.
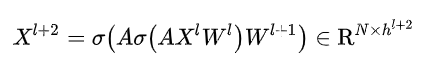
这样看来, 多层GCN中, 邻接矩阵是固定不变的,它依赖于拓扑图的构建. 我们要学习的只有转换矩阵的参数 , 通过反向传播即可学习更新.
2.4 添加自回环
返回刚刚的汇集邻居信息的地方. 前面提到的平均法, 加权平均法都忽略了自身节点的特征, 故在更新自身节点时, 一般会添加个自环,把自身特征和邻居特征结合来更新节点:
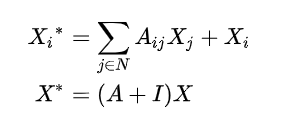
那么邻接矩阵和对应的度矩阵就变为:
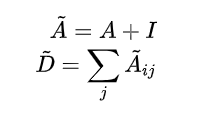
其中度数矩阵是一个对角矩阵 ，其中包含的信息为的每一个顶点的度数, 节点的度数定义为其边的权重的总和.
2.5 归一化
不同节点, 其边的数量和权重幅值都不一样, 比如有的节点特别多边, 这导致多边(或边权重很大)的节点在聚合后的特征值远远大于少边(边权重小)的节点. 所以需要在节点在更新自身前, 对邻居传来的信息(包括自环信息)进行归一化来消除这问题, 即为 , 所以聚合前后为:
2.6 对称归一化
上述的归一化只考虑了聚合节点 的度的情况, 但没有考虑到邻居 其节点的情况, 即未对邻居 所传播的信息进行归一化. (此处默认每个节点通过边对外发送相同量的信息, 边越多的节点,每条边发送出去的信息量就越小, 类似均摊. 防止部分交际花节点占据了大部分信息传播量)
采用几何平均数 来归一化, 即归一化为, 所以聚合前后为:
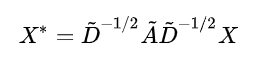归一化 是对 的行进行归一化, 对称归一化是对 的行和列分别进行归一化.
那么一层GCN的输入输出为:
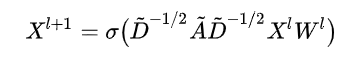
3. 谱域来解释GCN
借助图谱的理论来实现拓扑图上的卷积操作. 也是利用图的拉普拉斯Laplacian矩阵的特征值和特征向量来研究图的性质.
Graph Fourier Transformation及Graph Convolution的定义都用到图的拉普拉斯矩阵。频域卷积的前提条件是图必须是无向图，只考虑无向图，那么L就是对称矩阵. 拉普拉斯矩阵的定义: 其中 是度矩阵, 是邻接矩阵(取值{0,1}).
常见的拉普拉斯矩阵:
定义的Laplacian 矩阵更专业的名称叫Combinatorial Laplacian 定义的叫 Symmetric normalized Laplacian，很多GCN的论文中应用的是这种拉普拉斯矩阵. 定义的叫Random walk normalized Laplacian .
虽然GCN的核心基于拉普拉斯矩阵的谱分解, 我们待会再看其理论知识, 现在先从一个简单的类比例子加深拉普拉斯的印象.
3.1 简单的类比例子
我们用特例(图片像素点构造的拓扑图)来思考顶点域角度的GCN.
之前所说每个节点聚合邻居的节点值, 这和平滑空间滤波器的操作特别相似 (用于模糊处理或降低噪声,如均值滤波). 但是, 节点的一些突变信息也很重要(比如说破产/暴发户节点). 回想起锐化空间滤波器的知识, 知道微分算子的响应强度与突变程度成正比关系, 所以可以用微分来提取额外特征信息.
图片中, 二阶微分在增强细节上要比一阶微分好, 最简单的各向同性(旋转后结果不变)微分算子是拉普拉斯算子:
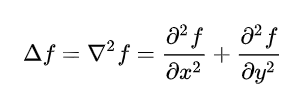
其中
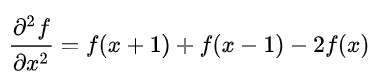
常用的一种拉普拉斯滤波器为(也是 ):
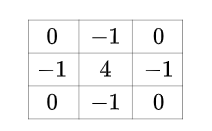
那我们 "理解" 了, 能提取图片的细节特征, 也能提取出节点的细节特征.
拉普拉斯算子(Laplacian operator) 的是空间二阶导, 是梯度的散度. 一般可用于描述物理量的流入流出。比如说在二维空间中的温度传播规律. 散度为正的点是“热源”，热量从其中流出；散度为负的点是“冷源”，热量流入该点.
tips:
采用拉普拉斯矩阵, 现在的论文方案可能不是说利用它来提取二阶微分信息,
而是认为拉普拉斯矩阵更能表达这个拓扑图, 其特征向量作为基函数更有代表性.
现在很多论文也对 L 进行各种魔改, 可能是想找到个更能适应任务代表拓扑图的矩阵.
3.2 拉普拉斯作用
滤波器通过卷积方法,能从图片中提取特征. 拓扑图也是. 卷积一般在傅里叶域中计算(时域卷积=频域相乘), 而为了满足傅里叶变换要求, 需要找到连续的正交基对应于傅里叶变换的基. 若拿到了正交基后, 就可以进行卷积操作(在傅里叶域中计算), 得到卷积结果了.
拉普拉斯矩阵恰好满足这些条件.
拉普拉斯是半正定实对称矩阵, 对称矩阵一定n个线性无关的特征向量 实对称矩阵具有n个特征值,所对应的n个特征向量相互正交 半正定矩阵特征值非负. n阶实对称矩阵L必可对角化, 且可用正交矩阵对角化。
那可以直接将拉普拉斯矩阵谱分解:
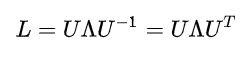
其中是n个特征值构成的对角矩阵,是单位特征向量(列向量)组成的矩阵. 是正交矩阵，满足
所以通过正交基 可以让卷积操作转到傅里叶域中进行, 从而能得到卷积后结果(即包含节点细节特征的输出).
3.3 Graph上的傅里叶变换
卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积，即对于函数 与 两者的卷积是其函数傅立叶变换乘积的逆变换:
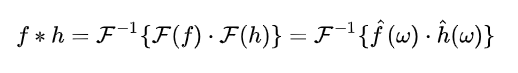
直接说结果:
表示对 进行傅里叶变换. 表示对 进行傅里叶逆变换. 故 和 的卷积结果为(Graph卷积公式, 是hadamard product内积运算)
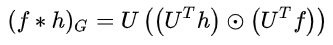
3.3.1 普通信号的傅里叶与逆变换
对于信号 , 其基函数, 传统傅里叶变换为:
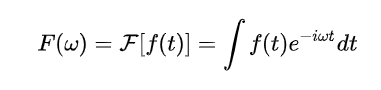
逆变换为:
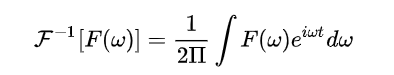
3.3.2 Graph上的傅里叶与逆变换
Graph上 维向量 , 其中 表示拓扑图上节点的特征向量.
拓扑图的拉普拉斯矩阵L的特征向量矩阵为 , 那么特征值 (频率)所对应的特征向量 可作为傅里叶变换中的一个正交基, 计算得到 的傅里叶变换(不考虑复数情况):
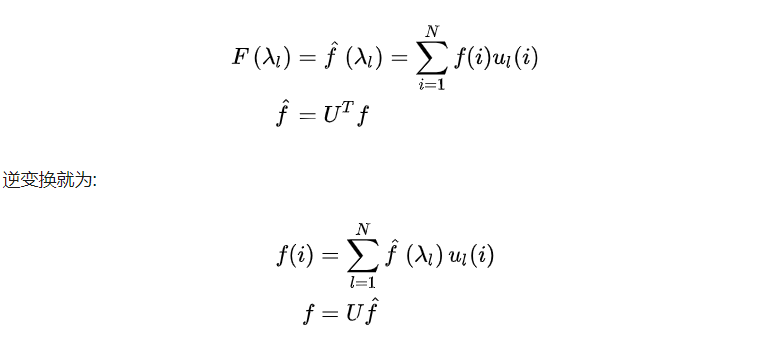
3.3.3 Graph的卷积结果
由上面可知, 和卷积核 的傅里叶变换结果 和 (均为列向量), 和 的卷积为 其分别傅里叶变换后的乘积的逆变换, 故Graph卷积公式为如下:
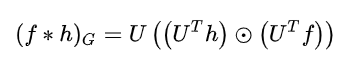
其中 是hadamard product（哈达马积), 即这两个向量进行内积运算(对应元素的乘积).
因为卷积核是自设计(或学习)的,可以将 的傅里叶变换 写成对角形式:
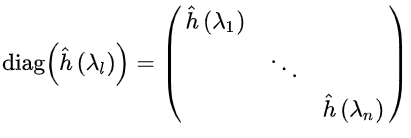其中 . (这可以理解为每个 提取一种频率上的信息).
所以Graph的卷积结果为(需要设计/学习的参数是 ):
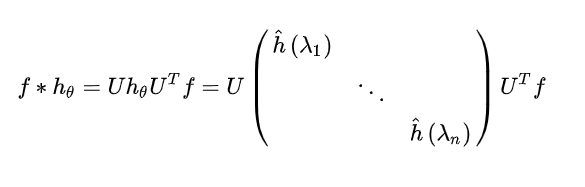
3.4 第一代GCN
论文 Spectral Networks and Locally Connected Networks on Graphs
直接将卷积核 从而让:
但弊端在于:
每次前传,都需要计算拉普拉斯矩阵的特征向量矩阵 , 以及 , , 的矩阵乘积, 计算代价高, 是 ; 不具有 spatial localization (类似感受野的意思, 这里只能用到 K=1 的邻居.); 需要 个参数(卷积核, 来提取各个频率的信息). 拓扑图大时计算量大,参数且多.
3.5 第二代GCN-ChebNet
论文 2016_NIPS_Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
将 用切比雪夫多项式去拟合, 利用Chebyshev多项式去拟合卷积核方法降低复杂度.
图卷积网络 GCN Graph Convolutional Network（谱域GCN）的理解和详细推导
如何理解 Graph Convolutional Network（GCN）？
图卷积网络(GCN)新手村完全指南
定义特征向量对角矩阵的切比雪夫多项式为滤波器：
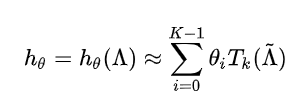而 可以通过 Chebyshev 多项式 的 K -th 阶截断展开来进行拟合， 并且 进行scale 使其元素位于 [-1,1]. . (因为原来的 处于 [0,2]). 这样缩放是为了满足 Chebyshev多项式展开的条件:自变量处于[-1,1]之间.
所以最后卷积情况为:
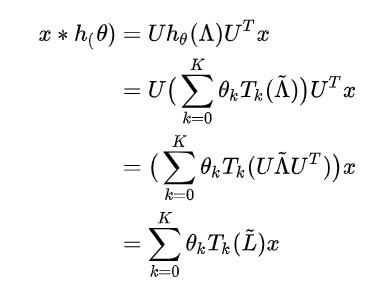
现在整个运算复杂度是, 式子是 K-localized(类比于感受野), 具有局部连接性.
3.6 一阶ChebNet
让GCN火起来的是这篇文章: 2017_ICLR_Semi-supervised classification with graph convolutional networks
当ChebNet一阶近似时, 让 , 那么ChebNet卷积公式简化近似为:
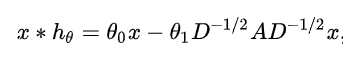
为了限制参数的数量以解决过度拟合, 并最小化每层的计算操作， 1-st ChebNet假设 ,图卷积的定义就近似为（简单一阶模型）：
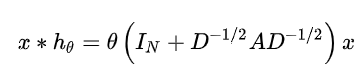
而 的特征值范围在 [0,2], 所以在深度神经网络中反复使用该算子将导致数值消失或爆炸问题(梯度爆炸或消失问题). 所以引入归一化技巧(renormalization trick):
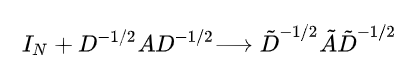
其中, , 即拓扑图加上自环.
所以论文中的快速卷积公式就是:
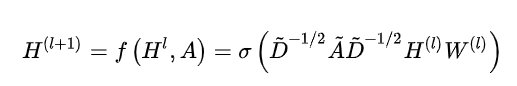
其中 是参数 矩阵, 为节点的特征向量. 计算复杂度也大大降低.
那么 ,就具有 维特征(每个节点具有 维特征向量)的 , 以及 个 卷积核参数时,
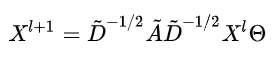
其中 是卷积核参数矩阵, 且 为新的特征向量. 计算复杂度为
注意, 此时该公式和 [GCN顶点域] 解释中的 [对称归一化] 公式完全一样.
到这里, GCN的原理就算大致介绍完毕了. 下面简略介绍下 一阶ChebNet 以及其他一些GCN论文的应用吧.
4.GCN的应用
4.1 一阶ChebNet的应用
在半监督的节点分类任务中, 可以构建两层的GCN 来完成.
计算邻接矩阵 , 后得到. 每个节点的最后 output 是 维特征向量(对应为 类):
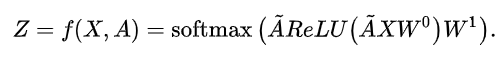
其中 , 是可学习参数, 将标签传给交叉熵就可以让网络进行学习了.
我们看看论文中提供的表格, 加深我们对不同 Propagation (及公式) 的感受.
4.2 学习类别Graph特征与视觉向量对齐 (ZeroShot)
2018_CVPR_Zero-shot Recognition via Semantic Embeddings and Knowledge Graphs
构建知识图谱, 每个节点代表一个类, 利用多层的GCN进行不同类间的信息迁移.
GCN中采用归一化后的 Binary 邻接矩阵. 代码中查得采用对称归一化邻接矩阵, 即传播模式为:
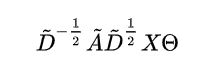
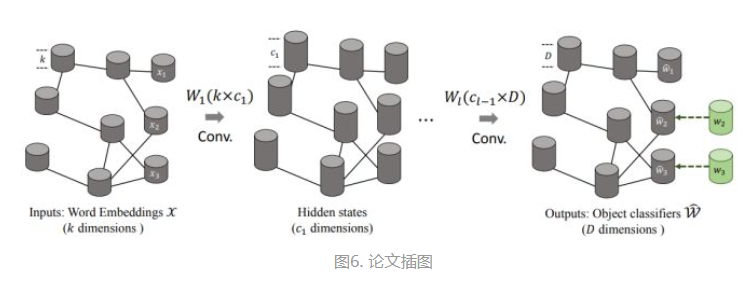
GCN的输入是每类的Word Embedding 向量, 最后一层的输出维度 和视觉向量的维度一致. 通过 均方误差(MSE) 来训练让节点最后的输出和对应的视觉向量相近.
采用的数据集是 Imagenet, 类别间的关系可从Imagenet官网中提取.
4.3 构建加权的密集图_信息传播更广且避免平滑_与视觉向量对齐(ZeroShot)
2019_CVPR_Rethinking Knowledge Graph Propagation for Zero-Shot Learning
简单地叠加普通GCN层虽然能让知识的传播范围增广, 但也容易让节点平滑(稀释了知识), 而降低了性能. 该文章提出一种密集设计的图, 让远距离(但有关系)的节点之间能直接连接进行传播.
简单地说, 以前都是亲兄弟节点才有联系(连线), 如果想让那些表表表亲戚的信息传播过来, 需要叠加GCN层, 这样会导致信息稀释(或说平滑). 而该论文就直接让同一个血缘(或说比较亲的血缘关系)的大家族都有线相连接(设置不同的权重), 那浅层的GCN网络就可以让远方亲戚的信息传播过来.
本文基于节点之间的距离学习权重. 明确利用知识图的层次结构，构建密集连接结构. 节点汇集信息时分为"从祖先辈获得的信息"和"从子孙辈获得的信息"阶段.
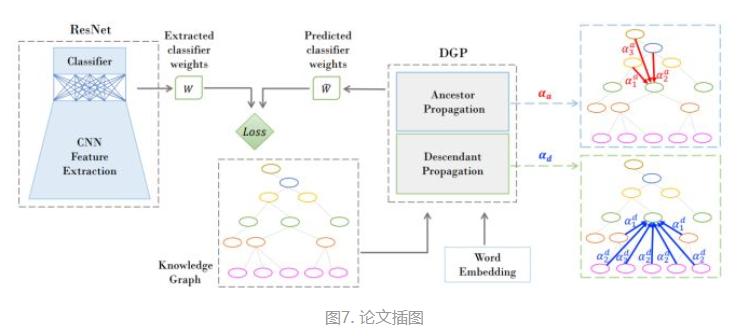
由于传播时文中定义"先从子辈汇聚信息", 再从"父辈汇聚信息", 所以本文的GCN传播为:
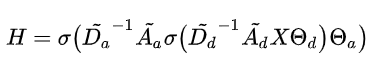
定义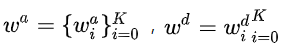
表示可学习参数来获得ancestor 和 descendant的权重, K 表示 K -hops的距离. 那么就可以让边的权重
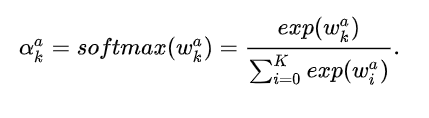
重新修改GCN传播方式:
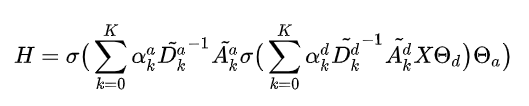
训练时的步骤为:
第一步, 训练图卷积网络DGP, 让其来预测CNN最后的FC层权重(即对齐视觉向量), 用均方误差. 第二步, 让DGP预测值替代FC的视觉权重, 从而微调CNN网络.
4.4 GCN网络的改进-残差结构与扩张卷积
2019_CVPR_Oral_Can GCNs Go as Deep as CNNs?
CNN的成功的一个关键因素是能够设计和训练一个深层的网络模型。但多层 GCN 会导致提取消失, 导致定点过度平滑, 让顶点特征值收敛到一致的值, 导致目前 GCN 架构都非常浅. 而且,浅层GCN 的感受野有限.
故本文借助CNN的概念, 把 Residual, Dense connections (残差,密集连接) 和 dilated convolutions(扩张/空洞卷积) 应用到GCN架构中.
几种结构
残差结构中, 通过逐点加法, 让节点(经过GCN得到的)残差特征, 加上节点原来的特征, 作为最后的节点新特征:
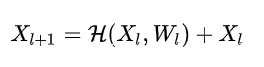
遇到维度不一致问题, 则跟残差网络一样进行转换(用GCN). 那么密集连接类似上述公式一样处理.
扩张卷积中, 每个GCN层后用 Dilated k-NN去寻找扩张邻居, 并构建扩张图, 在训练时采用随机扩张的方式(按概率进行扩张聚合). 其他细节的从CNN类比过来即可.
GCN的聚合函数
一般GCN中的聚合函数是 sum aggregator, 将邻域信息直接相加, 而同时也有 mean aggregator(和sum相像,归一化后的sum), max-pooling, attention, LSTM 等等聚合方式.
本文采用的是 简单无参数的max-pooling顶点特征聚集器. GCN结构是带BN+ReLU 的MLP.
Dynamic Edgs
GCN在训练中, 图结构一般是保持不变的. 有研究表明, 与具有固定图结构的GCN相比，动态图卷积可以更好地学习图的表示.
让节点的边动态变化, 能 有助于缓解过度平滑问题, 也能产生较大的感受野. 本文中每一层特征空间中通过 Dilated k-NN 来重新计算顶点之间的边, 来动态变化拓扑图.
虽然有改进, 但是计算成本较高.
4.5 GCN的改进-图注意力网络GAT
2018_ICLR_Graph Attention Networks
GCN局限有: 难处理动态图; 难分配不同的权重给不同的neighbor.
其实GAT是GNN的改进, 与GCN类似, 只是它是基于self-attention的图模型.
本文: 对不同的相邻节点学习分配相应的权重, multi-head多头的Attention结构, 计算注意力系数
对于顶点 , 逐个计算它的邻居和之间的相似系数:
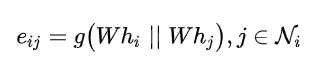
即先用共享参数 对顶点进行增维, 后拼接(concatenate)两个特征, 通过映射函数 将高维特征映射到一个Attention实数上.
通过对 的邻居进行softmax, 就可以得到(学习出)节点间的关系系数:
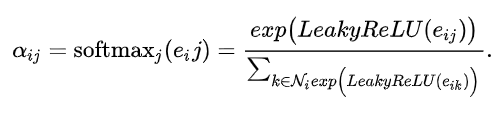
加权求和 aggregate
一般来说,聚合方式一般将邻居传来特征进行加权求和, 即可更新本节点的特征:
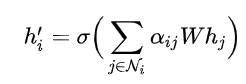
本文中增强了集合的方式, 采用 K 个注意力机制, 即用了K种邻居加权方式, 来更新本节点特征. 即Attention中的multi-head思想:
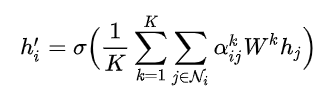
欢迎指正讨论 ~