FcaNet：从频域角度重新思考注意力机制-技术圈

点击左上方蓝字关注我们

全网搜集目标检测相关，人工筛选最优价值内容

编者荐语

一般来说，网络越深，所提取到的特征就越抽象；网络越宽，其特征就越丰富；基数越大，越能发挥每个卷积核独特的作用；而注意力则是一种能够强化重要信息抑制非重要信息的方法。

作者 | 湃森

链接 | https://zhuanlan.zhihu.com/p/339215696

一、论文信息

标题：《FcaNet: Frequency Channel Attention Networks》

作者：Zequn Qin et al.（浙江大学李玺团队）

文章：FcaNet: Frequency Channel Attention Networks

源码：暂未开源

二、导读

从网络结构本身的角度出发，可以从以下四个维度来提升卷积神经网络的性能，分别是：深度（ResNet）、宽度（WideResNet）、基数（ResNeXt）和注意力（SENet）。一般来说，网络越深，所提取到的特征就越抽象；网络越宽，其特征就越丰富；基数越大，越能发挥每个卷积核独特的作用；而注意力则是一种能够强化重要信息抑制非重要信息的方法，也是本文重点阐述的对象。

本文先回顾并总结到目前为止比较有代表性的注意力机制方法，同时对FcaNet进行解读。作者从频域角度切入，弥补了现有通道注意力方法中特征信息不足的缺点，将GAP推广到一种更为一般的表示形式，即2维的离散余弦变换DCT，通过引入更多的频率分量来充分的利用信息。对于每个特征通道图，本质上我们可以将其视为输入图片在不同卷积核上所对应的不同分量，类似于时频变化，相对于我们用卷积操作对输入信号（图片）进行傅里叶变换，从而将原始的输入分解为不同卷积核上的信号分量。

三、前情回顾

注意力机制，其本质是一种通过网络自主学习出的一组权重系数，并以“动态加权”的方式来强调我们所感兴趣的区域同时抑制不相关背景区域的机制。在计算机视觉领域中，注意力机制可以大致分为两大类：强注意力和软注意力。由于强注意力是一种随机的预测，其强调的是动态变化，虽然效果不错，但由于不可微的性质导致其应用很受限制。与之相反的是，软注意力是处处可微的，即能够通过基于梯度下降法的神经网络训练所获得，因此其应用相对来说也比较广泛。软注意力按照不同维度（如通道、空间、时间、类别等）出发，目前主流的注意力机制可以分为以下三种：通道注意力、空间注意力以及自注意力（Self-attention）。

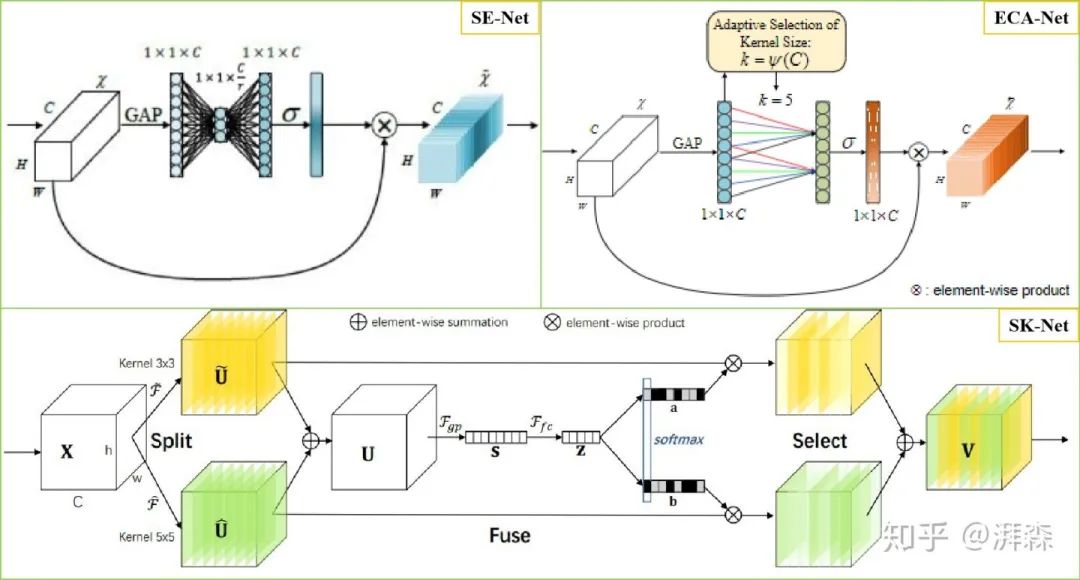
通道注意力

通道注意力旨在显示的建模出不同通道（特征图）之间的相关性，通过网络学习的方式来自动获取到每个特征通道的重要程度，最后再为每个通道赋予不同的权重系数，从而来强化重要的特征抑制非重要的特征。这方面的代表作有SE-Net，通过特征重标定的方式来自适应地调整通道之间的特征响应。此外，还有比较出名的SK-Net，则是受Inception-block和SE-block共同启发，从多尺度特征表征的角度考虑，通过引入多个卷积核分支来学习出不同尺度下的特征图注意力，让网络能够更加侧重于重要的尺度特征。另外还有ECA-Net，利用1维的稀疏卷积操作来优化SE模块中涉及到的全连接层操作来大幅降低参数量并保持相当的性能。为了压缩参数量和提高计算效率，SE-Net采用的是“先降维-再升维”的策略，利用两个多层感知机来学习不同通道之间的相关性，即当前的每一个特征图都与其它特征图进行交互，是一种密集型的连接。ECA-Net则简化了这种连接方式，令当前通道只与它的k个领域通道进行信息交互。

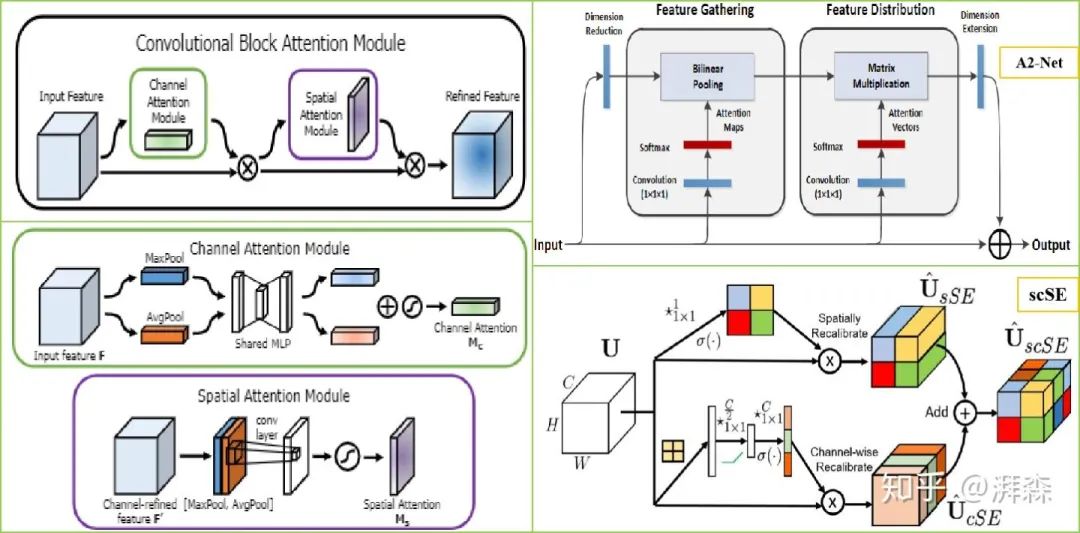
空间注意力

空间注意力旨在提升关键区域的特征表达，本质上是将原始图片中的空间信息通过空间转换模块，变换到另一个空间中并保留关键信息，为每个位置生成权重掩膜（mask）并加权输出，从而增强感兴趣的特定目标区域同时弱化不相关的背景区域。这方面比较出色的工作有CBAM，它是在原有通道注意力的基础上，衔接了一个空间注意力模块（SAM）。SAM是基于通道进行全局平均池化以及全局最大池化操作，产生两个代表不同信息的特征图，合并后再通过一个感受野较大的7×7卷积进行特征融合，最后再通过Sigmoid操作来生成权重图叠加回原始的输入特征图，从而使得目标区域得以增强。总的来说，对于空间注意力来说，由于将每个通道中的特征都做同等处理，忽略了通道间的信息交互；而通道注意力则是将一个通道内的信息直接进行全局处理，容易忽略空间内的信息交互。作者最终通过实验验证先通道后空间的方式比先空间后通道或者通道空间并行的方式效果更佳。此外，类似的改进模块还有A2-Net所提出的Double Attention模块以及受SE-Net启发而提出的变体注意力模块scSE等等。

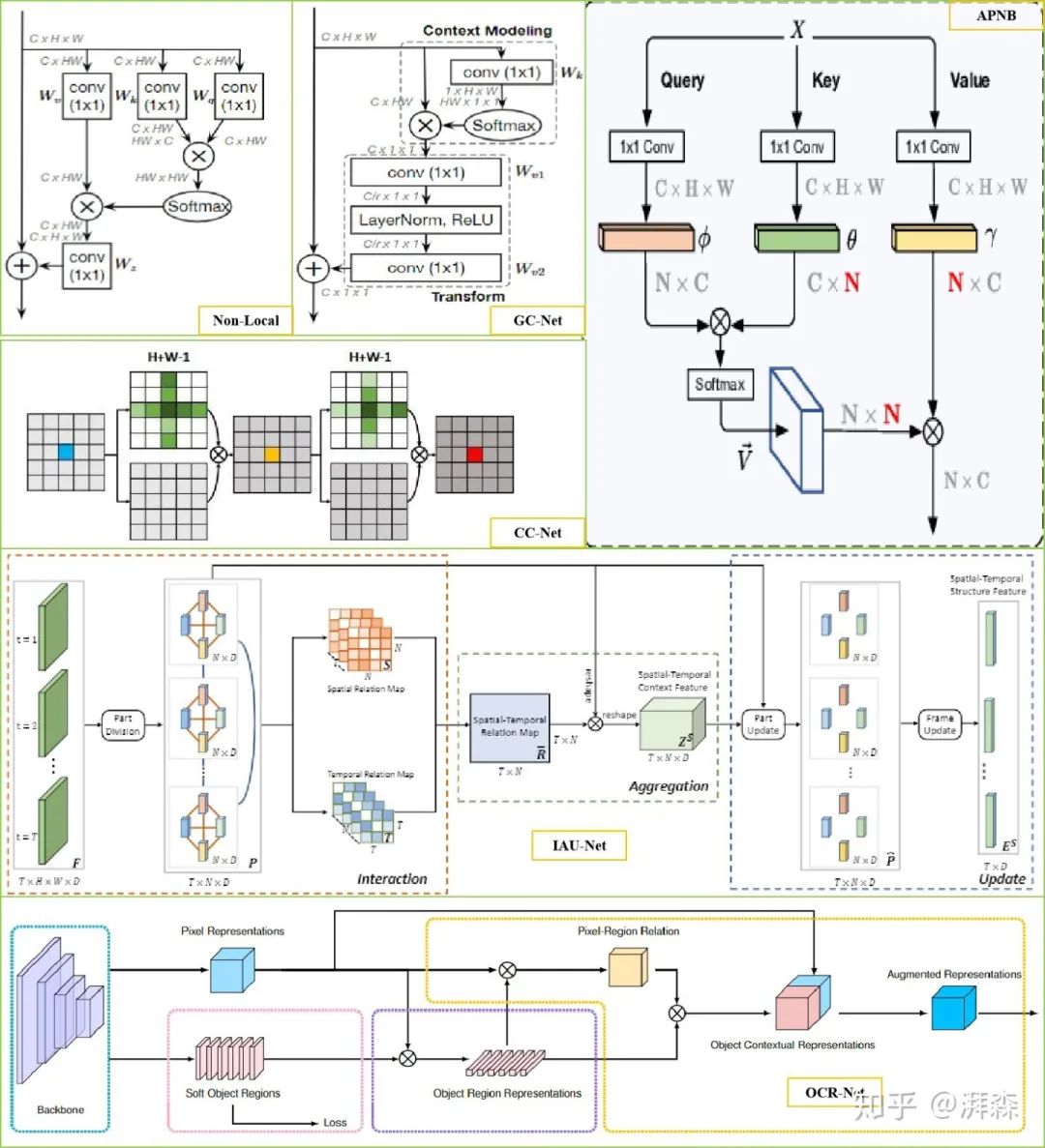
自注意力

自注意力是注意力机制的一种变体，其目的是为了减少对外部信息的依赖，尽可能地利用特征内部固有的信息进行注意力的交互。早期出现于谷歌所提出的Transformer架构当中。后来，何凯明等人将其应用到CV领域当中并提出了Non-Local模块，通过Self-Attention机制对全局上下午进行建模，有效地捕获长距离的特征依赖。一般的自注意力流程都是通过将原始特征图映射为三个向量分支，即Query、Key和Value。首先，计算Q和K的相关性权重矩阵系数；其次，通过软操作对权重矩阵进行归一化；最后再将权重系数叠加到V上，以实现全局上下文信息的建模。自NL-block提出后，也有许多基于它的改进。比如DANet提出的双重注意力机制是将NL思想同时应用到空间域和通道域，分别将空间像素点以及通道特征作为查询语句进行上下文建模。另一方面，虽然NL中利用了1×1卷积操作来压缩特征图的维度，但这种基于全局像素点（pixel-to-pixel）对的建模方式其计算量无疑是巨大的。因此，有许多工作也致力于解决这个问题，如CCNet开发并利用两个十字交叉注意力模块来等效的替代基于全局像素点对的建模；非对称金字塔非局部块体(Asymmetric Pyramid Non-local Block, APNB)以点对区域建模的方式来降低运算复杂度；GC-Net也结合了SE机制并提出使用简化的空间注意模块，取代原来的空间下采样过程。除此之外我们也可以从区域对区域建模的角度对其进行更进一步地优化。除了从空间、通道维度进行优化外，我们还可以从时间、类别角度进行改进，这方面的工作分别有IAU-Net和OCR-Net。

CNN中的注意力机制盘点

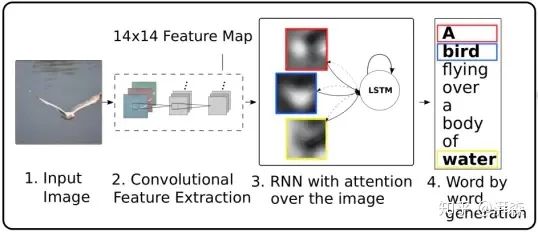
《Show, Attend and Tell: Neural Image Caption Generation with Visual Attention》

受机器翻译中的Attention机制启发，Bengio等人于2015年在ICML上发表的一篇文章，首次将注意力机制应用大图像描述（Image Caption）领域，同时提出硬注意力和软注意力两种机制，并利用可视化的技术来直观的表达了Attention机制的作用，为后续注意力机制在计算机视觉领域的发展开了先河。

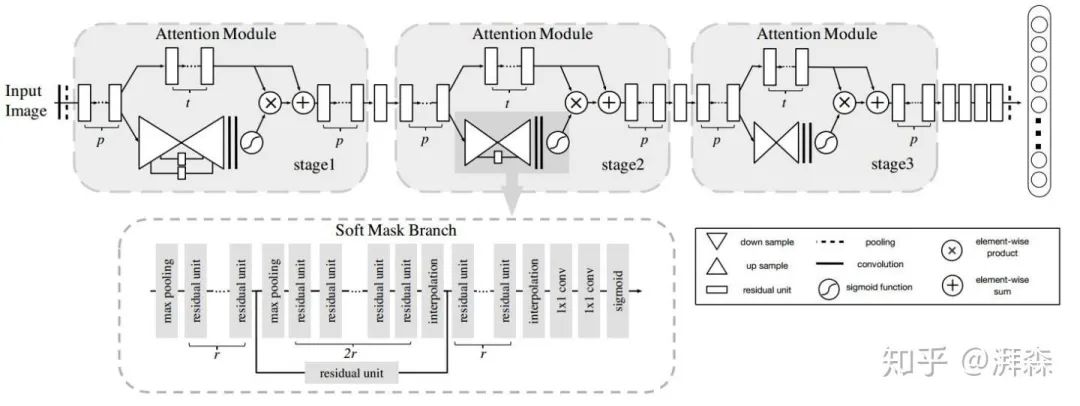
《Residual attention network for image classification》

商汤科技和港中文于2017年发表在CVPR上的一篇文章提出了一种利用下采样和上采样空间注意机制的残差注意力网络。在此之前，以往的Attention模型大多应用于图像分割和显著性检测任务，出发点在于将注意力集中在部分感兴趣区域或显著区域上。作者利用这种模式，在常规的分类网络中，引入侧边分支，该分支同样是由一系列卷积和池化操作来逐渐地提取高级语义特征并增大网络的感受野，最后再将该分支直接上采样为原始分辨率尺寸作为特征激活图叠加回原始输入。遗憾的是，该方法提升效果好像并不明显，而且由于引入大量额外的参数，导致计算开销非常大。

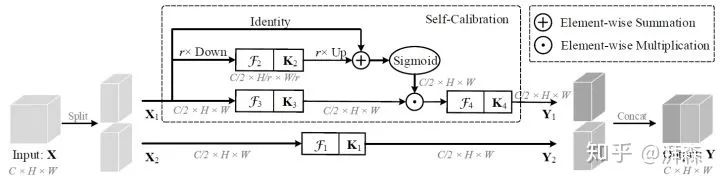
《Improving Convolutional Networks with Self-Calibrated Convolutions》

这是由南开大学程明明团队发表于2020年CVPR上的一篇文章，像这种通过先下采样来扩大感受野再上采样回去充当注意力图的方式与上面这篇论文的思路有点重复了，只不过将其从网络分支迁移到卷积分支，按理来说如果有引用下比较恰当。不过熟悉程老师【知乎ID：@程明明】的工作的可以发现，他们大多数的工作都非常简洁高效，而且大力提倡开源这一点很是佩服，大家有兴趣的可以直接去官网的Publications访问。

这篇文章是胡组长继SE-Net后于2018年在NIPS上发表的一篇文章，本文从上下文角度出发，提出了SE的更一般的形式GE，即Gather和Excite，并利用空间注意力来更好的挖掘特征之间的上下文信息。其中，Gather操作用于从局部的空间位置上提取特征，Excite操作则用于将其进行缩放还原回原始尺寸，是一种类似于编解码即Encoder-Decoder模型，可以以很小的参数量和计算量来提升网络的性能，不过知名度和影响力好像远不及SE。

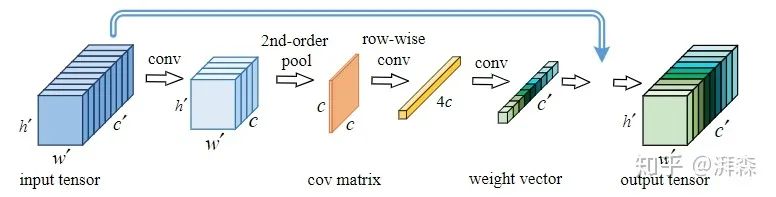
Global Second-order Pooling Convolutional Networks

GSoP-Net是发表于CVPR 2019年的一篇文章，作者认为CNN的主要目标是表征高维空间中数千个类别的复杂边界，学习高阶表示对于增强非线性建模能力至关重要。然而，传统的一阶网络显然不能够有效的表征，因此作者从底层到高层逐步引入全局的二阶池化模块，通过对整体图像信息的相关性建模，来捕获长距离的统计信息，充分利用到了图像的上下文信息。与SE等操作提倡的利用2维的GAP操作不同，GSoP通过引入协方差来计算通道之间的关系。具体来说，在利用卷积和池化进行非线性变换以后，该协方差矩阵不仅可以用于沿通道维度进行张量的缩放，也可以用于沿空间维度进行张量缩放。整体来说，通过应用GSoP可以充分利用到图像中的二阶统计量，以高效的捕获全局的上下文信息。

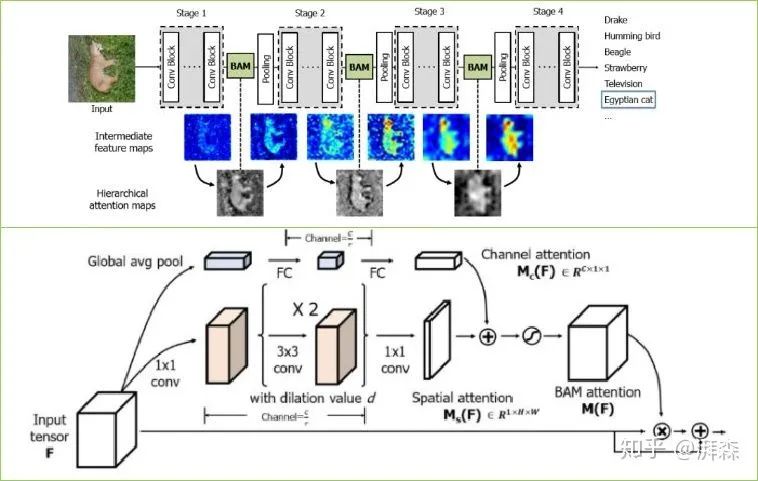
BAM是发表于BMVC 2018上的一篇文章，是由CBAM原班人马打造的，作者提出了一个简单可是有效的注意力模型，它能够结合到任何前向传播卷积神经网络中，同时经过两个分离的路径，即空间和通道，去获得注意力图。有趣的是，作者将其放置到了主干网络中每个Stage的中间，通过可视化的中间过程图我们可以明显的看出，BAM形成了一种分层的注意力机制，抑制背景特征，使模型能更加聚焦于前景特征，从而加强高级语义。BAM是通过将两个注意力分支进行串联求和，而CBAM则是一种并联的形式。类似的双重注意力模式还有DA-Net和scSE注意力，有兴趣的可以自行查看。

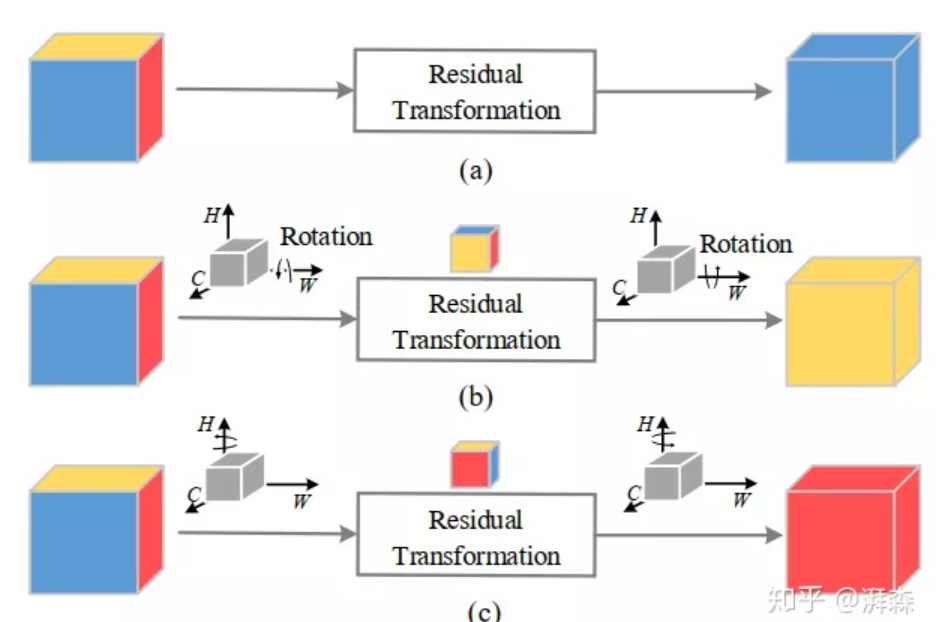
Rotate to Attend: Convolutional Triplet Attention Module

这是由印度小哥最新提出来的一个工作，作者从维度交互的角度出发，提出了一种三重注意力，即Triplet Attention。传统的注意力方式是通过GAP操作计算出一个权值系数，然后利用这个系数对原始的输入特征图进行统一缩放。其实这里也反复提到，GAP是在二维空间层面上对输入张量进行分解，浓缩为一个系数，不可避免的会导致空间细节信息的大量缺失。而且，单纯的在通道上进行操作，也容易忽略掉空间上一些关键的信息。虽然后面BAM和CBAM的出现缓解了通道和空间的依赖关系，但本质上这两者还是独立的，只不过是将其串联或并联起来。于是乎，印度小哥提倡要让不同维度之间的信息互相交互起来，比如有三个维度，HWC，那就让它们两两进行交互即可。不过说实话，个人感觉这工作有点鸡肋，随意的维度交互有时会破坏信息的空间一致性，结果反而得不偿失，这工作还不如GC-Net来的实在，结合SE操作直接对Non-local进行简化，通俗易懂，简洁高效，欢迎打脸。

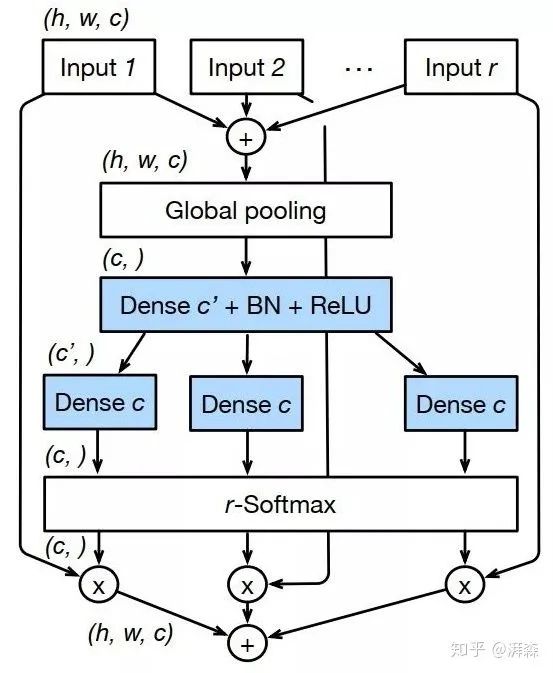
ResNeSt，号称ResNet的强化版，是由李沐团队张航博士（知乎ID：@张航

）所提出来的一篇文章，作者从基数维度出发，将注意力的思想融入到多分支卷积结构当中，来解决传统CNN感受野受限以及却反跨通道信息交互的问题，遗憾的是刚被ECCV 2020拒了。

ResNeSt整体延续了“Split-Transfore-Merge”结构，有点SK（知乎ID：

@李翔）的味道，综合SENet、SKNet与ResNeXt三者的思想。

ResNeSt所呈现的效果确实非常惊艳的，在ADE20K、MS-COCO等数据集上屠榜，碾压其他的手动网络架构，没有额外的计算开销，代码也不是很复杂。

尽管出来后许多人质疑其性能的提升跟大量的trick有很大关系且一开始代码实现有点问题，但不妨碍我们学习其思想，毕竟做科研不像搞开发，工程侧重的是talk is cheap, show me your code，而研究侧重的是code is weak, show me your idea.

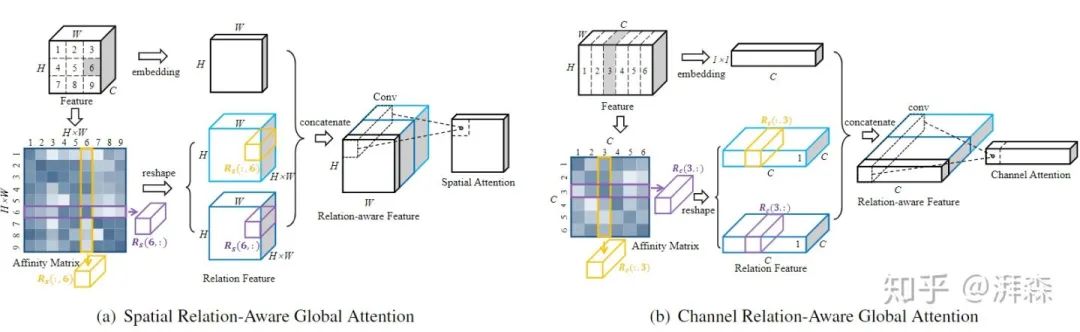
《Relation-Aware Global Attention for Person Re-identification》

Relation-Aware Global Attention是中科大&微软亚洲研究院发表于CVPR 2020上针对行人重识别任务所提出的一种注意力方法。本文提倡的观点是，要直观地判断一个特征节点是否重要，就应该知道全局范围的特性，这样便可以通过得到进行决策所需要的关系信息，来更好地探索每个特征节点各自的全局关系，从而更好地学习注意力。

四、论文解读

4.1 动机

通常来说，由于有限的计算资源开销，类似通道注意力机制这种通过网络学习的方式来获得权重函数需要对每个通道的标量进行计算，而全卷平均池化操作由于其易用性和高效性无疑是最佳的选择。尽管如此，但存在一个潜在的问题是GAP无法很好地捕获丰富的输入模式信息，因此在处理不同的输入时缺乏特征多样性。因此，也出现了一个自然而然的问题，即均值信息是否足以代表通道注意力中不同的特征通道。作者从三个角度进行分析：

首先，从特征通道本身的角度出发，不同特征度表征不同的信息，而GAP操作，即“平均”操作会极大的抑制特征的这种多样性；
其次，从频率角度分析，GAP等价于离散余弦变换（DCT）的最低频率分量。因此，如果仅使用GAP，显然会忽略掉许多其它有用的频率分量；
最后，以CBAM论文中所提出的观点去支撑论证，即单纯的使用GAP不足以表达特征原有的丰富信息。

4.2 贡献

证明了GAP是DCT的特例。在此基础上，将GAP推广到频域中，并提出了多光谱通道注意力框架——FcaNet；
通过探讨使用不同数量的频率分量及其不同组合的影响，提出了选择频率分量的两步准则；
广泛的实验表明，该方法在ImageNet和COCO数据集上均达到了最佳水平。在以ResNet-50为骨干网络的基础上，同时在相同参数量和计算量的情况下，所提出方法在ImageNet上的Top-1精度方面可以比SENet高出1.8%；
所提出方法不仅有效还非常简单，只需在现有的通道注意力实现中修改一行代码即可

4.3 方法

4.3.1 通道注意力和离散余弦变换回顾

通道注意力：

离散余弦变换：

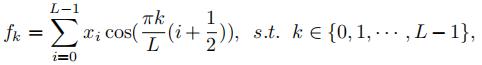
这里为DCT的频谱，表示输入，L为输入分量的长度。此外，二维的DCT可以表示为：

同样地，这里和分别表示输入分量的高度和宽度，后面半部分为对应的DCT权重。相应地，我们可以写出它的逆变换：

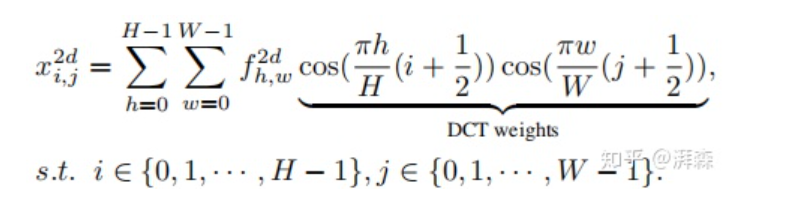Inverse 2D-DCT

为简化运算和便于叙述，作者后面移除了一些归一化因子常量。从以上公式可以看出GAP是现有通道注意力方法的预处理方式；而DCT可以看作是输入的加权和，其中余弦部分表示其对应的权重。因此，我们可以将GAP这种均值运算当做是输入的最简单频谱，如上所述，仅使用单个GAP不足以表征所有的特征信息，作者下面便引入了多光谱通道注意力的方法。

DCT属于Singal Porcessing领域的范畴，是JPEG图像压缩算法里的核心算法。没学过信号处理的估计看起来有些吃力，建议可以简单预习下这门课，了解一些基本概念，然后学习下傅里叶变换，而DCT实际上便是限定了输入信号的DFT，或者说是DFT的一种特例。要还是对数学很抗拒的话可以简单的认为DCT实际上的作用便是获得更好的频域能量聚集度，说白了就是将图像中相对重要的信息凝聚在一起，最简单的理解就是可以聚焦。说到这里，相信各位童鞋都似懂非懂了吧，“聚焦”不就是注意力干的事情吗？作者就是将这个思想用到了这里，Maths is important！

作者到这里就结束了，当然根据求和的可分性准则，我们也可以将2维DCT改写成如下形式：

更一般我们还能写成矩阵相乘形式：，其中为变换系数矩阵。

4.3.2 多光谱通道注意力框架的推导及频率分量的选取准则

作者首先抛出了一个定理：GAP是2维DCT的特例，其结果与2维DCT的最低频率分量成比例。

假设2维DCT中的和为0，则可以推导出以下式子：

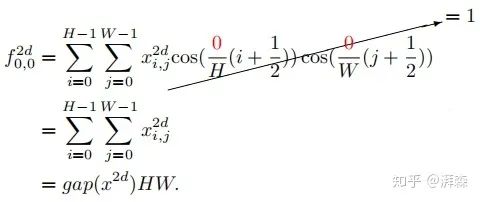
注：cos(0)=1. 上述左式为2维DCT的最低频率分量，可以看出它与GAP是成正比关系的。证明了这点之后，接下来要考虑的事情便是如何将其他频率分量整合到通道注意力机制当中。根据上述公式，我们将2维DCT的逆变换重写成以下形式：

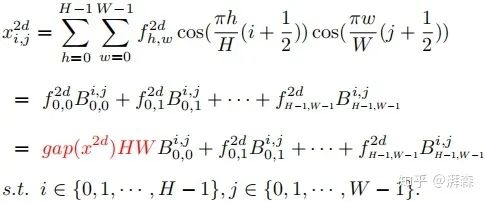
这里表示的是频率分量，也可以理解为DCT的权重分量。根据上述公式，我们很自然地将图像特征分解为不同频率分量的组合。可以看出，GAP操作仅利用到了其中的一个频率分量。

Illustration of existing channel attention and multi-spectral channel attention.

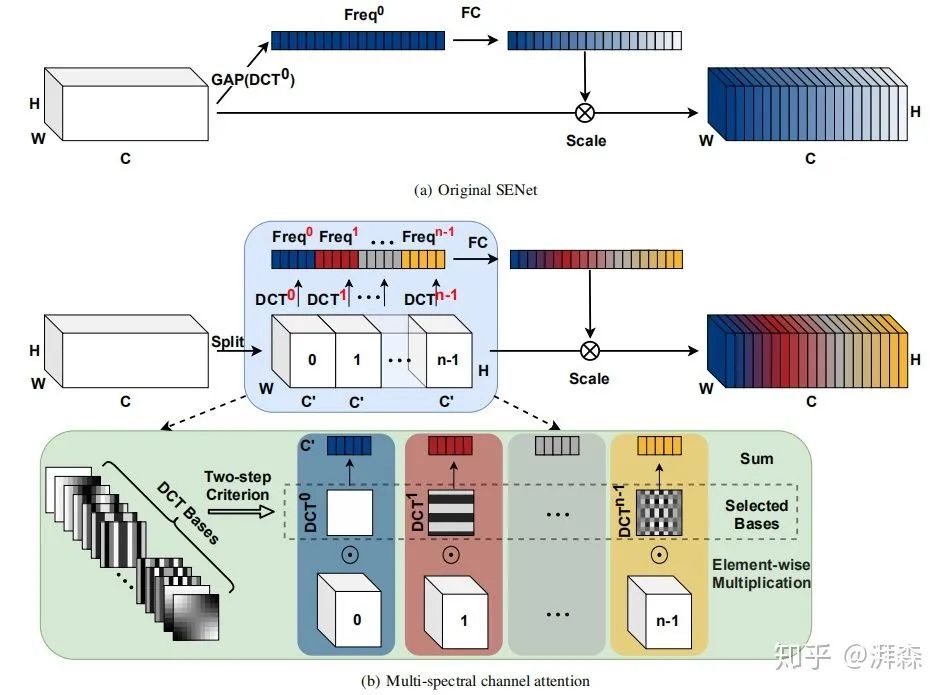
上图为原始SE模块与作者所提出的MCA模块对比示意图。上面提到，为了引入更多的信息，作者建议使用2维的DCT来融合多个频率分量，包括最低的频率分量，即GAP。具体操作流程为：首先，将输入按通道维度划分为n部分，其中n必须能被通道数整除。对于每个部分，分配相应的二维DCT频率分量，其结果可作为通道注意力的预处理结果（类似于GAP）：

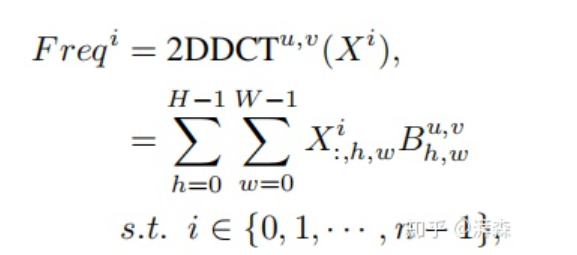
紧接着，我们可以将各部分的频率分量合并起来：

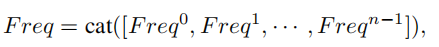
这里，即为的多光谱向量。因此，整个MCA框架可以表示如下：

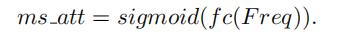
接下来阐述下频率分量的选取标准。对于每一部分，关键在于频率分量指数[u，v]的选择。对于空间尺寸为的每个通道特征，我们可以利用2维的DCT将其分解为个频率分量，于是总的频率分量应该为。举个例子，以ResNet-50骨干网络的输出为例，可以达到2048。因此，测试所有组合计算代价是非常昂贵的也没有必要，作者在这里给出了一种两步准则来选择MCA模块中的频率分量。其主要思想是为：

第一步先分别计算出通道注意力中每个频率分量的结果；
第二步再根据所得结果筛选出Top-k个性能最佳的频率分量。

至于如何衡量每个频率分量的性能作者在这里并没有阐述。虽然在后面4.2节中消融实验部分有提及到，但作者在此处简单

4.3.3 方法的有效性讨论、复杂度分析以及代码的实现

方法有效性讨论

上述我们分析了现有的通道注意力方法使用GAP作为预处理方式实际上是丢弃掉了除最低的频率分量的其他频率分量信息。作者在频域上推广了此方法，在MAC框架中自然地嵌入了更多的频率分量信息。之前有不少的工作也证明了CNN中存在着许多冗余的特征，比如Ghost-Net和OctaveConv等，所以当两个通道特征存在高度的相似性时，GAP操作会得到相似的结果。然而，在MCA框架中，由于不同的频率分量包含不同的信息，因此可以从冗余通道中提取更多的信息。

复杂度分析

作者从参数量和计算量两方面分析了所提出方法的复杂度。首先，由于2维DCT操作涉及到的权重是通过预先计算出来的一组常数，因此相比于原始的通道注意力方法如SE而言，没有引入额外的参数量。其次，计算量方面MCA仅仅比SE高出了略微的代价，可以忽略不计。

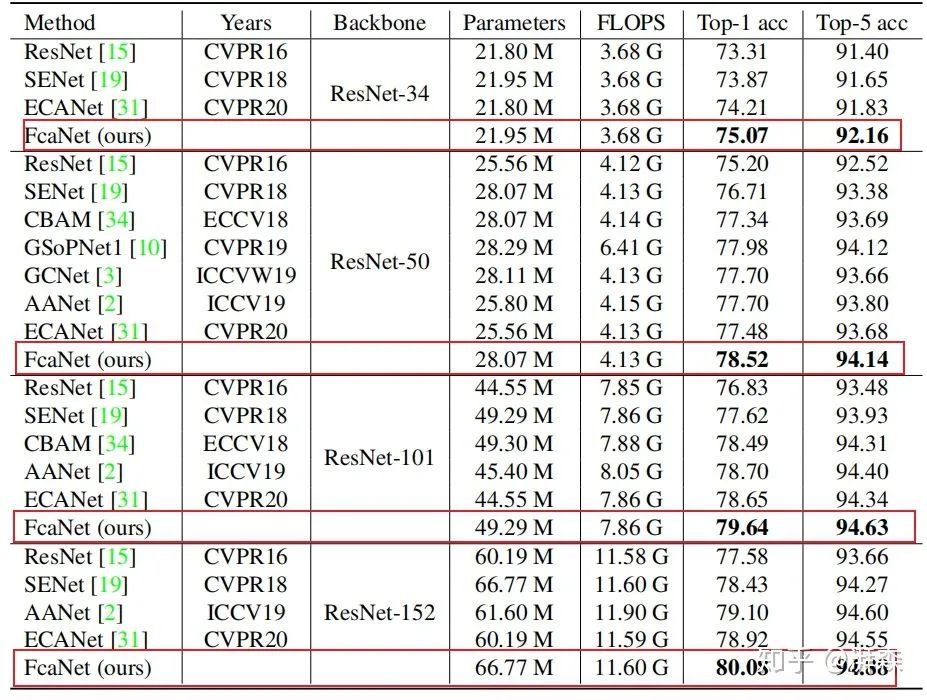
Comparison of different attention methods on ImageNet.

作者补充说“All other results are quoted from their original papers if available.”这样子的话存在不少问题，就是算着现在硬件算力的提升，性能也会更好一点，而且作者在实验过程也应用了《Deep residual learning for image recognition》和《Bag of tricks for image classifification with convolutional neural networks》这两篇文章所涉及的trick。严谨一点的话应该基于同一实验条件下进行公平的比较，所得到的结果会比较客观一点，或许相对其他rival的提升就不是 large margin，而是trivial contributions。

代码实现

2维DCT可以看作是输入的加权和，因此，可以通过简单地元素乘法以及求和运算来实现：

4.4 实验

4.4.1 消融实验

单个频率分量的有效性

为了研究不同频率分量对信道注意的影响，每次只使用一个单独的频率分量。考虑到ImageNet上最小的特征图大小为7×7，作者这里将整个2维的DCT频率空间划分为7×7部分，这样的话共有49组实验。为了加快实验速度，首先训练了一个100个epoch的标准ResNet-50网络作为基准模型。然后再将通道注意力添加到具有不同频率分量的基准模型中，以验证其效果。随后，基于同样的实验设置，以0.02的学习率对添加后的模型进行20轮的训练微调。

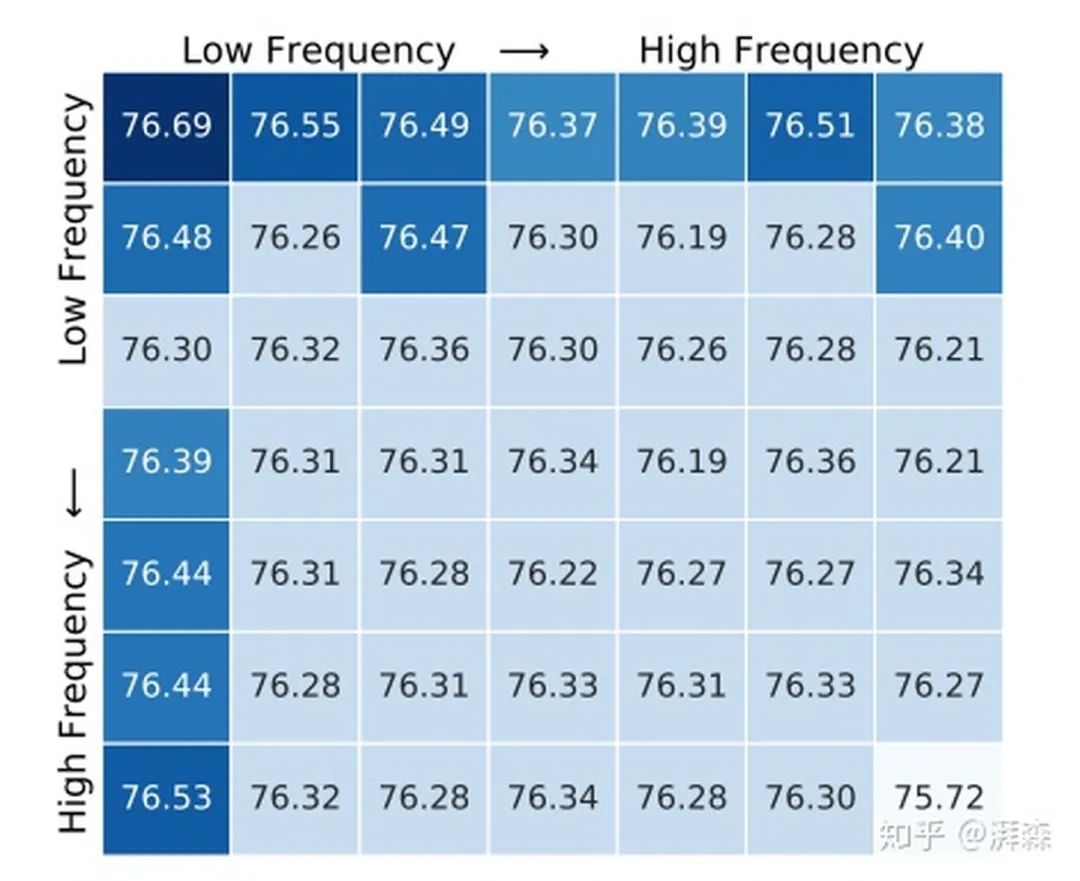
Top-1 accuracies on ImageNet using different frequencycomponents in channel attention individually.

实验结果如上所述，可以看出，当 [u, v]分量为[0, 0]时，效果是最好的，对应SE-Net的GAP操作，同时也验证了DNN偏好低频信息的结论。虽然如此，但结果也表明了其他频率分量对网络也是有贡献的，这意味着我们可以将这些信息给嵌入进去。

频率分量个数对性能的影响

在获得每个频率分量性能后，第二步是确定MCA模块所选择的最佳频率分量数。为了简单起见，作者选取了Top-k最高性能的频率成分，其中k可以是1、2、4、8、16或32等2的倍数。

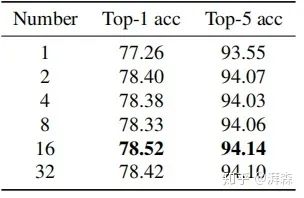
从实验结果可以看出，所有应用了多光谱的结果都要比单纯的GAP（对应Number=1）提高不少，实验的最佳效果是N=16，即选择16个频率分量，不过其他整体相差也不大。

4.4.2 与其他SOTA模型对比

作者在分类、检测和分割任务上与其他主流的通道注意力模型进行了比较：

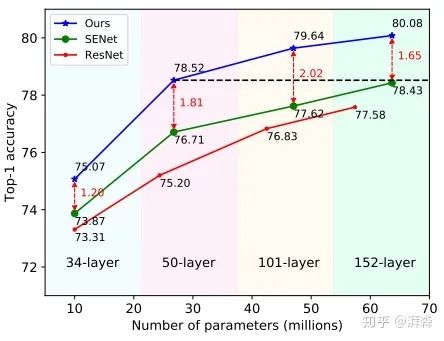
在分类任务上分别以ResNet-34, ResNet-50, ResNet-101, and ResNet-152四个骨干分支进行测试，结果显示Fca-Net在不同骨干网络上的TOP-1精度分别优于SE-NET 1.20%、1.81%、2.02%和1.65%。同时，在计算代价非常小的前提下，性能也优于GSOPNET。
在检测任务上以Faster-RCNN和Mask-RCNN作为检测器的前提下也显著的优于其他方法。
除了目标检测外，作者还在实例分割任务上测试了所提方法，然而这部分差距不是很明显。

附录

不同频率分量组合策略的研究

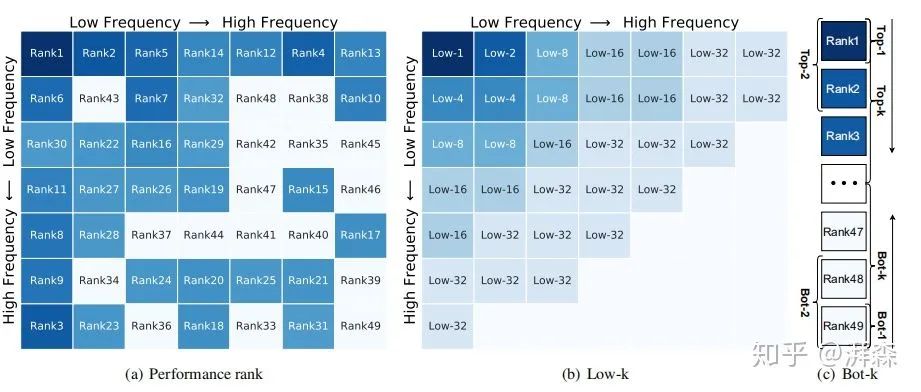
Illustration of different frequency combinations.

在消融实验部分，作者的two-step选择准则中的第二步是选择Top-k个性能表现组好的频率分量。在附录部分，作者还做了两组其他的组合策略，分别是选择如上图(b)左上角所示的所有频率分量，即low-1,low-2,...,low-32;还有一组是选择性能表现最差的Top-k个频率分量：

The results of Low-k combinations and Bot-k combinations.

从实验结果可以看出，Top-k性能最差的频率组合明显低于选择低频频率分量的组合策略，这也充分验证了低频分量是重要的，即DNN更加关注低频分量。当然，最佳的实验效果还是选择性能表现最好的Top-k个分量。

离散余弦变换的可视化

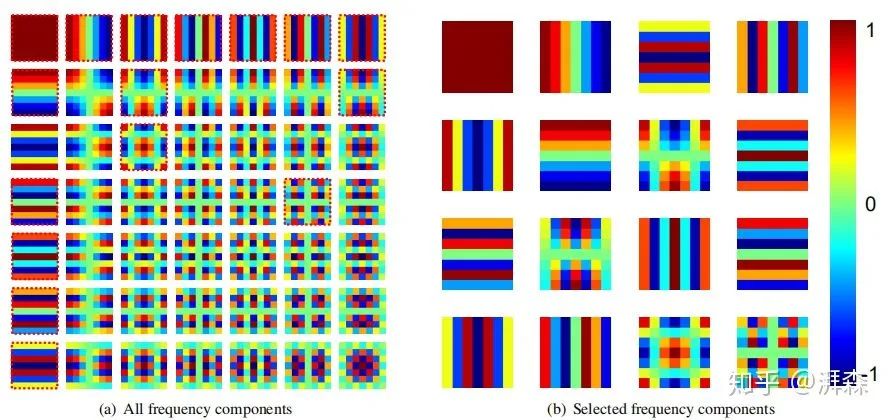
The visualization about DCT basis functions.

从上图可以看出，2维DCT的基函数是由规整的水平和垂直余弦波所组成，这些基函数是彼此正交的，与数据无关。此外，根据两步准则所选定的频率分量可以看到，所选择的频率分量通常是低频的。

DCT的初始化代码

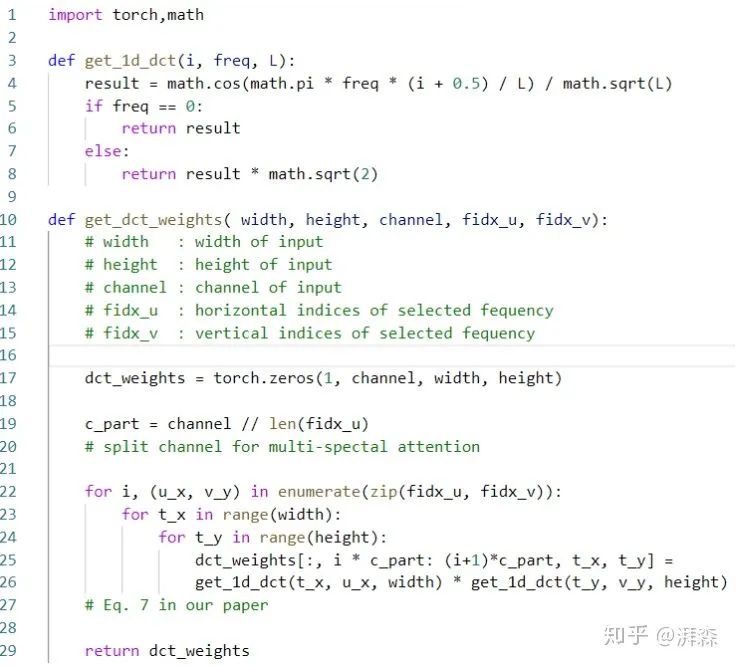
总结

最近也有不少文章开始从频域角度来切入大家有兴趣可以去了解下，比如阿里在CVPR 2020所提出来的文章，好像用的也是DCT？虽然作者一直强调他们的方式效果非常显著，代码量仅需一行。但从其描述的实验结果来看，作者似乎并没有严格按照统一条件下去进行对照组实验，而是直接摘抄其他方法原论文的结果报告出来。其次，一行代码这个也有点牵强，真正起作用的核心代码被封装起来，只不过是简单的使用了一个开关进行调用，严格意义上来说应该不算。整体来说，这篇文章的思路还是挺不错的，至于性能等后面源码公开出来留待时间的检验，投个最近的ICCV应该是稳了。

总结下Attention机制的优势有如下三点：参数少 ● 速度快 ● 效果好。现如今发表的许多注意力机制相关的方法，很多都是基于原始方法进行改进，至于改进的力度和效果提升见仁见智。虽然这里面大部分的提升很可能来自于大量的trick没报告出来，或者是由于数据泄露导致的unfair，又或者实验比较对象的巧妙选取等，但是不得不佩服的是作者们八仙过海各显神通讲故事的逻辑，从中也受益良多。很有意思的是，为了克服现在越来越内卷的顶会投稿量避免Reviewer看起来千篇一律直接给你Early Reject，很多论文都许多对一些常规的操作进行名词渲染。好比1×1卷积应该叫投影函数（Project function）；两个同阶矩阵的相乘可以写成哈达姆积（Hadamard product）；求两个矩阵的相似度计算称为亲和（Affinity）计算等等。另一方面，大多数改进的方向都不约而同，大体上都是从不同维度、复杂度、时频域出发。比如维度方面有通道、空间、时间、类别等；复杂度方面主要是基于维度的基础上，优化其参数量和计算量；域方面主要就是从时域到频域的变换；当然，还有很多跨领域交叉的尝试，比如最近才在计算机视觉领域中大火的Transformer机制；亦或者将2D的注意力扩展到3D去等。其实，细细品尝其中的滋味，熟悉原理和了解整个CV发展的脉络之后会发现，处处皆idea，哪怕从原理上创新不来，随便来个排列组合再配合上讲story和写paper的功力，一大把顶会顶刊在向我们招手——投稿就像海洋，只有鼓起勇气投出去的人才有资格别接收。写了整整一下午，生活艰难，创作不易，拒绝白嫖，从你我做起。觉得有帮助的也请欢迎关注、点赞、收藏、喜欢、转发五连击，谢谢。

END

双一流大学研究生团队创建，专注于目标检测与深度学习，希望可以将分享变成一种习惯！

整理不易，点赞三连↓