【机器学习】线性回归:不能忽视的三个问题

前言

线性回归是比较简单的机器学习算法，很多书籍介绍的第一种机器学习算法就是线性回归算法，笔者查阅的中文书籍都是给出线性回归的表达式，然后告诉你怎么求参数最优化，可能部分同学会忽视一些问题，至少笔者忽视了。因此，本文重点介绍了平常容易忽视的三类问题，（1）线性回归的理论依据是什么，（2）过拟合意味着什么。 （3）模型优化的方向

目录

---

1、线性回归的理论依据是什么

2、过拟合意味着什么

3、模型优化的方向

4、总结

线性回归的理论依据

泰勒公式

若函数 f(x)在包含x0的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有(n+1)阶 导数 ，则对 闭区间 [a,b]上任意一点x，成立下式：

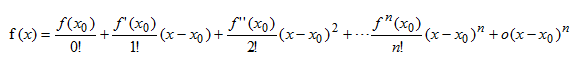
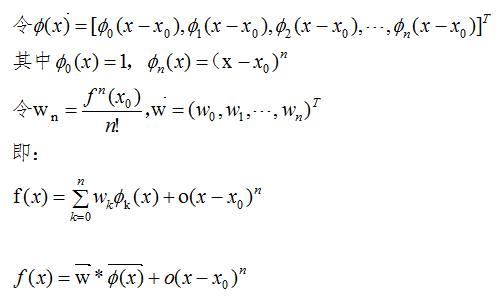
结论： 对于区间[a,b]上任意一点，函数值都可以用两个向量内积的表达式近似，其中

是基函数（basis function）， 是相应的系数。

高阶表达式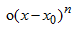表示两者值的误差（请回想您学过的线性回归表达式）。

傅里叶级数

周期函数f(x)可以用向量内积近似， 表示基函数， 表示相应的系数， 表示误差。

线性回归

由泰勒公式和傅里叶级数可知，当基函数的数量足够多时，向量内积无限接近于函数值。线性回归的向量内积表达式如下：

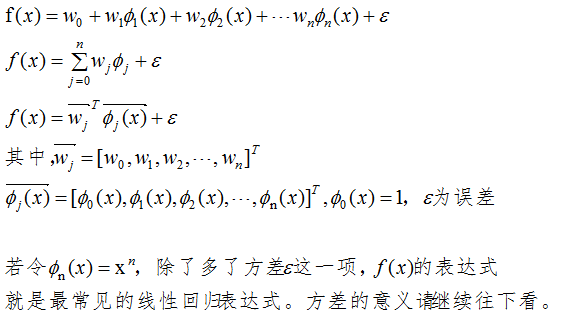
过拟合问题

过拟合定义

构建模型的训练误差很小或为0，测试误差很大，这一现象称为过拟合。

高斯噪声数据模型

我们采集的样本数据其实包含了噪声，假设该噪声的高斯噪声模型，均值为0，方差为。

若样本数据的标记为y1，理论标记为y，噪声为η，则有：

y1 = y + η，（其中，η是高斯分布的抽样）

上节的线性回归表达式的方差 表示的意义是噪声高斯分布的随机抽样，书本的线性回归表达式把方差也包含进去了。

过拟合原因

数学术语： 当基函数的个数足够大时，线性回归表达式的方程恒相等。

如下图：

机器学习术语：模型太过复杂以致于把无关紧要的噪声也学进去了。

当线性回归的系数向量间差异比较大时，则大概率设计的模型处于过拟合了。用数学角度去考虑，若某个系数很大，对于相差很近的x值，结果会有较大的差异，这是较明显的过拟合现象。

过拟合的解决办法是降低复杂度，后期会有相应的公众号文章，请继续关注。

模型的优化方向

模型的不同主要是体现在参数个数，参数大小以及正则化参数λ，优化模型的方法是调节上面三个参数（但不仅限于此，如核函数），目的是找到最优模型。

总结

本文通过泰勒公式和傅里叶级数的例子说明线性回归的合理性，线性回归表达式包含了方差项，该方差是高斯噪声模型的随机采样，若训练数据在线性回归的表达式恒相等，那么就要考虑过拟合问题了，回归系数间差异比较大也是判断过拟合的一种方式。模型优化的方法有很多种，比较常见的方法是调节参数个数，参数大小以及正则化参数λ。

参考：

Christopher M.Bishop <<Pattern Reconition and Machine Learning>>

                      
                                          往期
                                          精彩
                                          回顾
                                        
                                      

• 适合初学者入门人工智能的路线及资料下载
• (图文+视频)机器学习入门系列下载
• 机器学习及深度学习笔记等资料打印
• 《统计学习方法》的代码复现专辑
• 机器学习交流qq群955171419，加入微信群请 扫码