【机器学习:理论+实战】线性回归,你还只会调包吗?
自己动手实现线性回归
我们往往会用类似sklearn的linear_model模块直接调包去使用线性回归处理一些回归问题,但我们绝不能只会调包!
接下来我们就用面向对象的方式,自己实现一个线性回归类,并且在这个过程中体会从数学公式到python代码的美妙。
在这里我将不会讲解线性回归的原理和公式(毕竟这是python为主题的公众号),而是聚焦于”从公式到代码“的过程。所以如果对公式原理以及一些线性回归的相关术语不熟悉,可以去看相关的资料充充电,这并不难,毕竟线性回归是机器学习里最简单直观的算法了
简述线性回归模型
线性回归就是输入一堆数据(假设有m条,每条数据有n个属性,也就是m行n列),结果训练后得到模型参数(也就是线性回归方程中与每个属性相乘的那些值,有几n个属性,就有对应的n个参数)的过程。
训练的方法有许多,我大致分两类,一类就是正则方程,也就是直接通过解矩阵方程得到参数。另一类就是梯度下降,它又可以细分为批量梯度下降算法、随机梯度下降算法以及小批量梯度下降算法。梯度下降更加有通用性,因为其它机器学习模型的损失函数都极其复杂,无法获得最值的解析解,所以可以说正则方程法算是线性回归模型的”特色“。
设计自定义的线性回归类
初始化函数:
初始化函数接收参与训练的数据集,并且随机设定模型参数
getNormalEquation函数
正则方程函数
BGD函数
BGD函数是梯度下降算法的函数
SGD函数
SGD函数是随机梯度下降算法函数,接收学习率这个参数
MBGD函数
MBGD函数是小批量梯度下降算法的函数,接收学习率这个参数
train_BGD函数
用BGD算法训练,接收迭代率和学习率两个参数
train_SGD函数
用SGD算法训练,接收迭代率和学习率两个参数
train_MBGD函数
用MBGD算法训练,接收迭代率和学习率两个参数
Shuffle函数
这个函数主要用于生成与训练数据集大小相同的随机自然数序列。主要用于SGD函数和MBGD函数中,通过随机数序列打乱训练集和标签集,消除训练集顺序对SGD算法和MBGD算法的影响
Cost函数
这个函数就是平均训练的损失函数,计算训练数据集在模型参数下的预测结果与实际值之间的均方误差。它主要用于三个迭代训练函数中,记录每次迭代后的误差
predict函数
这个函数是预测函数,接受一组测试数据,然后结合模型参数对测试数据进行预测
test函数
这个函数和预测函数很相似,都是结合模型参数预测结果,不同的是这个函数接受的是测试数据集,它遍历整个测试数据集,每次都调用predict函数进行预测
自定义线性回归类的结构
import numpy as np
"""
这是一个关于线性回归的模块
核心部分就是LinearRegression这个类
这个类有以下几个方法
构造方法、根据参数计算预测值的方法、计算损失值的方法、生成随机数序列的方法、使用批量梯度下降、随机梯度下降、小批量随机梯度下降更新参数的方法
"""
class LinearRegress:
def __init__(self, input_data, real_result, theta):
def Cost(self):
def Shuffle(self):
def BGD(self,alpha):
def SGD(self,alpha):
def MBGD(self,alpha,batch_size):
def train_BGD(self,iter,alpha):
def train_SGD(self,iter,alpha):
def train_MBGD(self,iter,batch_size,alpha):
def predict(self,data):
def test(self,test_data):
初始化函数的代码实现
初始化函数__init__的参数是训练数据集input_data、训练结果集real_result以及参数theta。在初始化函数内,主要完成训练数据集、结果集以及模型参数的初始化,与此同时还要遍历每组数据,并且要对数据进行拓展,也就是增加一维常数属性1(因为线性回归方程都是z=ax+by+c这种类似形式,c前面的系数是1) 当theta的默认值是None,如果是None,那么就用正态分布随机给模型参数赋值,如若不是,就用theta作为模型参数
import numpy as np
class LinearRegress:
def __init__(self, input_data, real_result, theta):
"""
inputData :输入数据 (m条记录,n个属性,m*n)
realResult :真实数据 (m条记录,1个值,m*1)
theta :线性回归的参数,也就是这个算法不断更新迭代优化得到的核心数据 (对应n个属性,n*1)
默认为None 如果是None就用正态分布的数据来初始化参数,如果不是None,就用传进来的theta初始化参数
"""
# 输入数据集的形状
row, col = np.shape(input_data)
# 通过输入数据集,建立这个类里面的成员变量Data,先初始化为m个0组成的列表
self.Data = [0] * row
# 给m条数据中的每一条数据都添加上一个常数项1,这一步是为了与线性回归模型中的偏置b对应起来
for (index, data) in enumerate(input_data):
# 将每一条数据构成的列表后面都追加一个1.0,并且根据序号index将它们存放到成员变量Data相应位置中
self.Data[index] = list(data).append(1.0)
# 转化为numpy的格式更加高效
self.Data = np.array(self.Data)
# 通过输入的结果数据集,建立这个类中的成员变量Result
self.Result = real_result
# 如果参数不为None的时候,利用传入的theta初始化相应参数
if theta is not None:
self.Theta = theta
# 不然就用正态分布的数据来初始化
else:
# 此处选取了(n+1*1)的数据,也是为了和偏置匹配
self.Theta = np.random.normal((col + 1, 1))
辅助函数的编写
在前面一章我们已经提到了这个线性回归类的函数(方法)集合,我们先来看一看一些辅助函数,它们往往运用在其它的函数中,因此先对它们进行介绍。
Shuffle函数
功能:在运行SGD算法函数或者MBGD算法函数前,随机打乱原始的数据集以及对应的标签集。
def Shuffle(self):
"""
这是在运行SGD算法或者MBGD算法之前,随机打乱后原始数据集的函数
"""
# 首先获得训练集规模,之后按照规模生成自然数序列
length = len(self.InputData)
sequence = list(range(length))
# 利用numpy的随机打乱函数打乱训练数据下标
random_sequence = np.random.permutation(sequence)
# 返回数据集随机打乱后的数据序列
return random_sequence
Cost函数
功能:计算训练数据集self.InputData在模型参数self.Theta下的预测结果(也就是它们之间进行矩阵的乘法)与实际值之间的均方误差。主要运用在三种梯度下降算法函数中,记录每次迭代训练后的均方误差。
def Cost(self):
"""
这是计算损失函数的函数
"""
# 在线性回归里的损失函数定义为真实结果与预测结果之间的均方误差
# 首先计算输入数据的预测结果
predict = self.InputData.dot(self.Theta).T
# 计算真实结果与预测结果之间的均方误差
cost = predict-self.Result.T
cost = np.average(cost**2)
return cost
predict函数
功能:对输入的测试数据(1* n+1),结合模型参数(n+1* 1),作矩阵乘法获得预测结果
def predict(self,data):
"""
这是对一组测试数据预测的函数
:param data: 测试数据
"""
# 对测试数据加入1维特征,以适应矩阵乘法
tmp = [1.0]
tmp.extend(data)
data = np.array(tmp)
# 计算预测结果,计算结果形状为(1,),为了分析数据的方便
# 这里只返矩阵的第一个元素
predict_result = data.dot(self.Theta)[0]
return predict_result
test函数
功能:循环调用predict函数,遍历整个测试数据集,m条测试数据进行预测
def test(self,test_data):
"""
这是对测试数据集的线性回归预测函数
:param test_data: 测试数据集
"""
# 定义预测结果数组
predict_result = []
# 对测试数据进行遍历
for data in test_data:
# 预测每组data的结果
predict_result.append(self.predict(data))
predict_result = np.array(predict_result)
return predict_result
train_BGD函数
利用BGD算法函数进行训练的函数,iter代表迭代的次数,alpha代表学习率,也就是每次更新模型参数的幅度大小
def train_BGD(self,iter,alpha):
"""
这是利用BGD算法迭代优化的函数
:param iter: 迭代次数
:param alpha: 学习率
"""
# 定义训练损失数组,记录每轮迭代的训练数据集的损失
Cost = []
# 开始进行迭代训练
for i in range(iter):
# 利用学习率alpha,结合BGD算法对模型进行训练
self.BGD(alpha)
# 记录每次迭代的训练损失
Cost.append(self.Cost())
Cost = np.array(Cost)
return Cost
train_SGD函数
利用SGD算法函数进行训练的函数,参数说明同上
def train_SGD(self,iter,alpha):
"""
这是利用SGD算法迭代优化的函数
:param iter: 迭代次数
:param alpha: 学习率
"""
# 定义训练损失数组,记录每轮迭代的训练数据集的损失
Cost = []
# 开始进行迭代训练
for i in range(iter):
# 利用学习率alpha,结合SGD算法对模型进行训练
self.SGD(alpha)
# 记录每次迭代的训练损失
Cost.append(self.Cost())
Cost = np.array(Cost)
return Cost
train_MBGD函数
利用MBGD算法函数进行训练的函数,参数说明同上
def train_MBGD(self,iter,batch_size,alpha):
"""
这是利用MBGD算法迭代优化的函数
:param iter: 迭代次数
:param batch_size: 小样本规模
:param alpha: 学习率
"""
# 定义训练损失数组,记录每轮迭代的训练数据集的损失
Cost = []
# 开始进行迭代训练
for i in range(iter):
# 利用学习率alpha,结合MBGD算法对模型进行训练
self.MBGD(alpha,batch_size)
# 记录每次迭代的训练损失
Cost.append(self.Cost())
Cost = np.array(Cost)
return Cost
正则方程法
所谓正则方程法就是用矩阵求导的方法,求取损失函数的最小值 在求导的过程中,会求解导函数等于零的方程,最终将会解得模型参数值为:训练数据集的转置乘以训练数据集本身,之后对相乘结果求一个逆矩阵,再将整个逆矩阵乘以训练数据集本身,最后与结果数据集相乘。具体的推导过程可以看下图
值得注意的是,正则方程法需要保证训练数据集的转置乘以训练数据集本身,记为XT*X可以求得逆矩阵,但是在实际问题中,数据集的特征数n可能会大于数据集规模m,这就导致了XTX不可逆。故而在实际的编程过程中,会在XTX的基础上加一个很小的可逆矩阵,例如0.001E,这样就可以保证可逆了。
def getNormalEquation(self):
"""
这是利用正规方程计算模型参数Thetha
"""
"""
0.001*np.eye(np.shape(self.InputData.T))是
防止出现原始XT的行列式为0,即防止原始XT不可逆
"""
# 获得输入数据数组形状
col,rol = np.shape(self.InputData.T)
# 计算输入数据矩阵的转置
XT = self.InputData.T+0.001*np.eye(col,rol)
# 计算矩阵的逆
inv = np.linalg.inv(XT.dot(self.InputData))
# 计算模型参数Thetha
self.Theta = inv.dot(XT.dot(self.Result))
梯度下降算法
梯度下降算法是求取最值的通法,通过每次的迭代更新,逐步逼近最优解,常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。
在线性回归模型中,我们在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。
具体可分为三种:批量梯度下降算法(Batch Gradient Descent)BGD、随机梯度下降算法(Stochastic Gradient Descent)SGD 以及 小批量梯度下降算法(Mini Batch Gradient Descent)MBGD,下面我们来依次介绍这些算法的思想以及具体的编程实现。
批量梯度下降算法
算法流程:每次迭代遍历数据集时,保存每组训练数据对应的梯度增量,待到遍历结束后,计算所有梯度增量之和,再与当前模型参数相加,更新模型参数,重复上述过程,直到模型参数值收敛。显然,经过不断的优化迭代后,BGD算法几乎可以收敛于全局最优解(当然还受限于学习率这个超参数,它代表模型参数更新的幅度)。
def BGD(self,alpha):
"""
这是利用BGD算法进行一次迭代调整参数的函数
:param alpha: 学习率
"""
# 定义梯度增量数组
gradient_increasment = []
# 对输入的训练数据及其真实结果进行依次遍历
for (input_data,real_result) in zip(self.InputData,self.Result):
# 计算每组input_data的梯度增量,并放入梯度增量数组
g = (real_result-input_data.dot(self.Theta))*input_data
gradient_increasment.append(g)
# 按列计算属性的平均梯度增量
avg_g = np.average(gradient_increasment,0)
# 改变平均梯度增量数组形状
avg_g = avg_g.reshape((len(avg_g),1))
# 更新参数Theta
self.Theta = self.Theta + alpha*avg_g
BGD算法每次迭代都需要遍历整个训练数据集,保存每组数据对应的梯度增量,当数据规模较大时,会带来很大的空间开销。基于此,随机梯度下降算法 SGD 应运而生!
随机梯度下降算法
BGD算法虽然可以几乎收敛于全局最优解,但是开销太大,速度慢,适应性不强。究其原因,还是每次都要遍历整个训练数据集这个过程花销太大了,所以就想到了每次就用一条数据来更新参数的方法,这就是随机梯度下降算法!
算法流程:在规模为m的数据集中,每次取出一条,来计算对应的模型参数梯度,每次都用这个梯度来更新模型参数。也就是说在迭代过程中更新m次。重复上述过程直到收敛,在这个过程中会先讲数据集打乱。
这个算法与批量梯度下降的最大不同就是:前者需要累积整个数据集的梯度增量之和,而后再更新;而随机梯度下降则是将每条数据产生的梯度增量立即更新到模型参数上。后者的空间开销显然要小
def SGD(self,alpha):
"""
这是利用SGD算法进行一次迭代调整参数的函数
:param alpha: 学习率
"""
# 首先将数据集随机打乱,减小数据集顺序对参数调优的影响
shuffle_sequence = self.Shuffle()
self.InputData = self.InputData[shuffle_sequence]
self.Result = self.Result[shuffle_sequence]
# 对训练数据集进行遍历,利用每组训练数据对参数进行调整
for (input_data,real_result) in zip(self.InputData,self.Result):
# 计算每组input_data的梯度增量
g = (real_result-input_data.dot(self.Theta))*input_data
# 调整每组input_data的梯度增量的形状
g = g.reshape((len(g),1))
# 更新线性回归模型参数
self.Theta = self.Theta + alpha * g
然而,SGD也有其缺陷,虽然相比于BGD频繁调整了参数,加快了收敛速度,但是每次都用一条数据的梯度来更新,不能代表全体数据集的梯度方向,属实是”以偏概全“了,属于贪心算法,理论上不能获得最优解,常常只能获得次优解。基于SGD和BGD的优点不同,小批量随机梯度下降 MBGD 算法应运而生!
小批量随机梯度下降算法
这个算法的思想就是:首先打乱数据集顺序,并且划分为若干批小样本,而后每次迭代后遍历一个批次里的所有样本,计算梯度增量平均值,据此来更新模型参数。在小批量样本的规模足够大的时候,小批量样本的梯度向量平均值也近似等于整个训练数据集的平均值了,这样就结合了BGD的”广泛性“和SGD的”快速性“
def MBGD(self,alpha,batch_size):
"""
这是利用MBGD算法进行一次迭代调整参数的函数
:param alpha: 学习率
:param batch_size: 小样本规模
"""
# 首先将数据集随机打乱,减小数据集顺序对参数调优的影响
shuffle_sequence = self.Shuffle()
self.InputData = self.InputData[shuffle_sequence]
self.Result = self.Result[shuffle_sequence]
# 遍历每个小批量样本
for start in np.arange(0, len(shuffle_sequence), batch_size):
# 判断start+batch_size是否大于数组长度,
# 防止最后一组小样本规模可能小于batch_size的情况
end = np.min([start + batch_size, len(shuffle_sequence)])
# 获取训练小批量样本集及其标签
mini_batch = shuffle_sequence[start:end]
Mini_Train_Data = self.InputData[mini_batch]
Mini_Train_Result = self.Result[mini_batch]
# 定义梯度增量数组
gradient_increasment = []
# 对小样本训练集进行遍历,利用每个小样本的梯度增量的平均值对模型参数进行更新
for (data,result) in zip(Mini_Train_Data,Mini_Train_Result):
# 计算每组input_data的梯度增量,并放入梯度增量数组
g = (result - data.dot(self.Theta)) * data
gradient_increasment.append(g)
# 按列计算每组小样本训练集的梯度增量的平均值,并改变其形状
avg_g = np.average(gradient_increasment, 0)
avg_g = avg_g.reshape((len(avg_g), 1))
# 更新模型参数theta
self.Theta = self.Theta + alpha * avg_g
MBGD兼顾了BGD算法和SGD算法的优点,是中庸的选择
训练线性回归模型
在这个章节中,将会用sklearn内置的波士顿房价数据集结合我们自己实现的线性回归去预测波士顿郊区的房价。
波士顿房价数据集共有14个属性,其中13个是输入属性,还有1个属性是输出属性”房屋价格“。13个输入属性中的第6个属性就是”房间数目“,结合常识,房间数目约等于面积,对房价的影响很大。为了简化案例,我们就聚焦于”房间数目“,据此预测房屋价格。
波士顿房价数据集是很知名的数据集,如果对这个数据集的结构不了解的同学可以去搜一下相关资料。
在本章的代码中,会用到numpy、pandas、matplotlib以及sklearn,对这些模块不熟悉的同学,可以去看看蚂蚁老师的相关课程!
Merge函数:将实验数据转换为结构化数据
因为我希望将得到的实验结果存入到excel文件中,就先定义了Merge函数,将sklearn中的数据转换为pandas的dataframe形式,方便后续操作。
def Merge(data,col):
"""
这是生成DataFrame数据的函数
:param data:输入数据
:param col:列名称数组
"""
Data = np.array(data).T
return pd.DataFrame(Data,columns=col)
数据预处理
首先导入数据集,并且对它进行预处理,用load_boston()函数加载数据集,并且只选取第六个特征值”平均房间数目“,通过Merge生成dataframe,而后保存为excel文件。然后将改变一下训练数据集和结果(房价)数据集的形状,最后将这些数据集划分为训练集和测试集。
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
# 导入数据以及划分训练数据与测试数据
InputData, Result = load_boston(return_X_y=True)
# 为了方便实验,只取第6维特征。第6列为平均房间数目
InputData = np.array(InputData)[:,5]
# 保存原始数据集
Data = Merge([InputData,Result],['平均房间数目','房价'])
Data.to_excel('./原始数据.xlsx')
# 改变数据集与真实房价数组的形状
InputData = InputData.reshape((len(InputData), 1))
Result = np.array(Result).reshape((len(Result), 1))
# 把数据集分成训练数据集和测试数据集
train_data,test_data,train_result,test_result = \
train_test_split(InputData,Result,test_size=0.1,random_state=50)
数据可视化
我们会用到matplotlib库,对这些数据进行可视化
import matplotlib as mpl
import matplotlib.pyplot as plt
# 解决Matplotlib中的中文乱码问题,以便于后面实验结果可视化
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
# 利用散点图可视化测试数据集,并保存可视化结果
col = ['真实房价']
plt.scatter(test_data,test_result,alpha=0.5,c='b',s=10)
plt.grid(True)
plt.legend(labels = col,loc='best')
plt.xlabel("房间数")
plt.ylabel("真实房价")
plt.savefig("./测试集可视化.jpg",bbox_inches='tight')
plt.show()
plt.close()
构建模型
首先,随机生成模型参数,而后将训练数据和模型参数,引入我们的线性回归类,将训练数据和模型参数传入我们写好的线性回归对象中,每一种算法都实例化出一个对象。
from LinearRegression.LinearRegression import LinearRegress
# 开始构建线性回归模型
col = np.shape(train_data)[1]+1
# 初始化线性回归参数theta
theta = np.random.random((col,1))
# BGD优化的线性回归模型
linearregression_BGD = LinearRegression(train_data, train_result,theta)
# SGD优化的线性回归模型
linearregression_SGD = LinearRegression(train_data, train_result,theta)
# MBGD优化的线性回归模型
linearregression_MBGD = LinearRegression(train_data, train_result,theta)
# 正则方程优化的线性回归模型
linearregression_NormalEquation = LinearRegression(train_data, train_result,theta)
之后设定迭代次数、学习率、小批量样本个数这些超参数,并且传入相应的对象中
# 训练模型
iter = 30000 # 迭代次数
alpha = 0.001 # 学习率
batch_size = 64 # 小样本规模
# BGD的训练损失
BGD_train_cost = linearregression_BGD.train_BGD(iter,alpha)
# SGD的训练损失
SGD_train_cost = linearregression_SGD.train_SGD(iter,alpha)
# MBGD的训练损失
MBGD_train_cost = linearregression_MBGD.train_MBGD(iter,batch_size,alpha)
# 利用正规方程获取参数
linearregression_NormalEquation.getNormalEquation()
记录迭代训练误差结果并进行可视化
训练结束后,就将训练的结果进行可视化,观察比较算法之间的差异,并且将这些信息保存为excel文件
# 三种梯度下降算法迭代训练误差结果可视化,并保存可视化结果
col = ['BGD','SGD','MBGD']
iter = np.arange(iter)
plt.plot(iter, BGD_train_cost, 'r-.')
plt.plot(iter, SGD_train_cost, 'b-')
plt.plot(iter, MBGD_train_cost, 'k--')
plt.grid(True)
plt.xlabel("迭代次数")
plt.ylabel("平均训练损失")
plt.legend(labels = col,loc = 'best')
plt.savefig("./三种梯度算法的平均训练损失.jpg",bbox_inches='tight')
plt.show()
plt.close()
# 三种梯度下降算法的训练损失
# 整合三种梯度下降算法的训练损失到DataFrame
train_cost = [BGD_train_cost,SGD_train_cost,MBGD_train_cost]
train_cost = Merge(train_cost,col)
# 保存三种梯度下降算法的训练损失及其统计信息
train_cost.to_excel("./三种梯度下降算法的训练训练损失.xlsx")
train_cost.describe().to_excel("./三种梯度下降算法的训练训练损失统计.xlsx")
用训练好的模型拟合曲线
计算4种算法训练的线性回归模型的拟合曲线,并可视化
# 计算4种调优算法下的拟合曲线
x = np.arange(int(np.min(test_data)), int(np.max(test_data)+1))
x = x.reshape((len(x),1))
# BGD算法的拟合曲线
BGD = linearregression_BGD.test(x)
# SGD算法的拟合曲线
SGD = linearregression_SGD.test(x)
# MBGD算法的拟合曲线
MBGD = linearregression_MBGD.test(x)
# 正则方程的拟合曲线
NormalEquation = linearregression_NormalEquation.test(x)
# 4种模型的拟合直线可视化,并保存可视化结果
col = ['BGD', 'SGD', 'MBGD', '正则方程']
plt.plot(x, BGD,'r-.')
plt.plot(x, SGD, 'b-')
plt.plot(x, MBGD, 'k--')
plt.plot(x, NormalEquation, 'g:',)
plt.scatter(test_data,test_result,alpha=0.5,c='b',s=10)
plt.grid(True)
plt.xlabel("房间数")
plt.ylabel("预测值")
plt.legend(labels = col,loc = 'best')
plt.savefig("./预测值比较.jpg",bbox_inches='tight')
plt.show()
plt.close()
对模型进行验证
前文介绍了模型的训练过程,那如何评判训练好的模型效果呢?方法是用测试集了验证模型预测值与实际值的误差去判断效果。
在这里,将会使用4种实例化对象的test方法得到模型的预测结果,然后使用pandas将预测结果和统计信息保存为excel文件
# 利用测试集进行线性回归预测
# BGD算法的预测结果
BGD_predict = linearregression_BGD.test(test_data)
# SGD算法的预测结果
SGD_predict = linearregression_SGD.test(test_data)
# MBGD算法的预测结果
MBGD_predict = linearregression_MBGD.test(test_data)
# 正则方程的预测结果
NormalEquation_predict = linearregression_NormalEquation.test(test_data)
# 保存预测数据
# A.tolist()是将numpy.array转化为python的list类型的函数,是将A的所有元素
# 当作一个整体作为list的一个元素,因此我们只需要A.tolist()的第一个元素
data = [test_data.T.tolist()[0],test_result.T.tolist()[0],BGD_predict,
SGD_predict,MBGD_predict,NormalEquation_predict]
col = ["平均房间数目","真实房价",'BGD预测结果','SGD预测结果','MBGD预测结果','正规方程预测结果']
Data = Merge(data,col)
Data.to_excel('./测试数据与预测结果.xlsx')
# 计算4种算法的均方误差以及其统计信息
# test_result之前的形状为(num,1),首先计算其转置后
# 获得其第一个元素即可
test_result = test_result.T[0]
# BGD算法的均方误差
BGD_error = ((BGD_predict-test_result)**2)
# SGD算法的均方误差
SGD_error = ((SGD_predict-test_result)**2)
# MBGD算法的均方误差
MBGD_error = ((MBGD_predict-test_result)**2)
# 正则方程的均方误差
NormalEquation_error = ((NormalEquation_predict-test_result)**2)
# 整合四种算法的均方误差到DataFrame
error = [BGD_error,SGD_error,MBGD_error,NormalEquation_error]
col = ['BGD', 'SGD', 'MBGD', '正则方程']
error = Merge(error,col)
# 保存四种均方误差及其统计信息
error.to_excel("./四种算法的均方预测误差原始数据.xlsx")
error.describe().to_excel("./四种算法的均方预测误差统计.xlsx")
分析本次实验的结果
原始数据集
我们来看看原始数据集长什么样子
可视化测试集
看表格不直观,我们来看看其中测试集的可视化结果吧!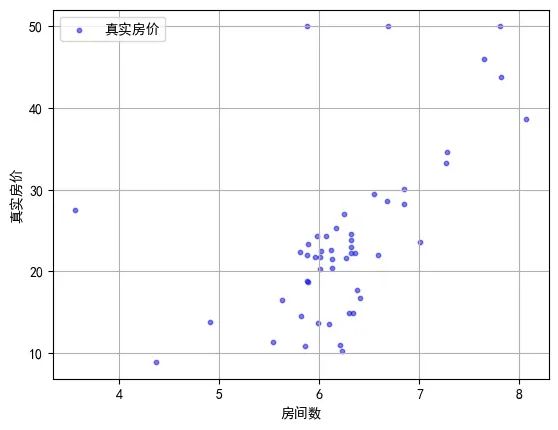
可以明显看到平均房间数和房价之间存在正相关的关系
对比3种梯度下降算法在训练过程中的平均损失
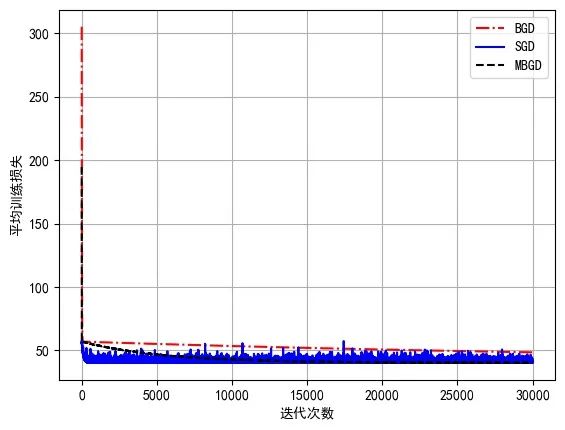
对3种梯度下降算法的均方误差进行统计
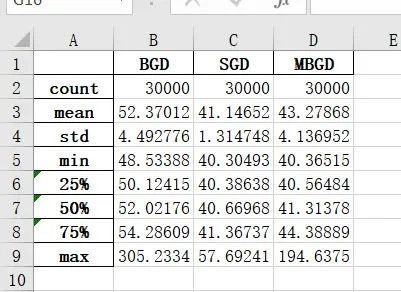
显然可以发现,BGD算法的敛速度最慢,且在训练结束后,BGD算法的训练均方误差最终在48.533,SGD的收敛速度最快(最快到达拐点),但由于贪心算法的特性(每条数据的梯度增量都作用于模型参数)它会在最小值附近震荡,而MBGD收敛速度居中,且没有震荡,误差基本上都是一路下跌
这些结果和我们的前期判断一致
验证模型
接下来我们看看4中算法训练出来的模型应用在测试集的数据上是什么效果吧!
预测结果可视化
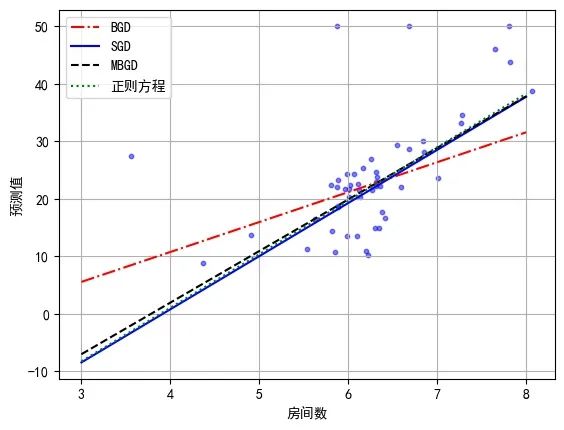
在上图中,圆点代表真实数据,从上到下4条线形不一的直线分别代表BGD、SGD、MBGD以及正则方程算法训练出来的线性回归模型的预测拟合直线。从图中来看,除了少量离群点,绝大多数点都均匀分布在4条拟合直线的左右,大致可以判定,效果都还不错。
预测结果量化分析
为了更好地对比4中算法的优缺点,下图给出测试集的预测房价与真实房价之间的均方误差统计信息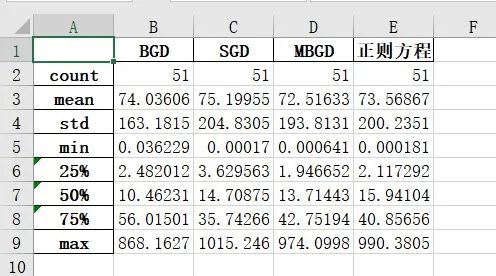
可以看出来,MBGD的均方误差在测试集上是最小的,正则方程紧随其后,BGD第三,SGD误差最大 再次验证了我们之前的判断。
总结
线性回归是机器学习回归问题中最简单的模型,其模型参数通常用梯度下降和正则方程求解。在三种梯度下降算法中,BGD能近似获得全局最优解,稳定性强,但是收敛速度慢;SGD则是收敛速度快,但无法获得全局最优解,且稳定性欠佳;MBGD则是中庸方案。至于正则方程,则适用于大规模的数据集,但其时间复杂度较大(涉及大量矩阵相乘)。
推荐我的机器学习实战课程
一个机器学习系列,从模型训练到在线预估,到Linux线上部署,包含大量的工程细节,推荐给大家我自己的机器学习实战课程:
扫码购买
《机器学习 Sklearn二手车价格预估》
课程介绍

购买后加老师微信:ant_learn_python
会提供微信答疑,拉VIP会员交流群
