AF-GCL：不需要增强的图对比学习-技术圈

来源：Paperweekly
本文共3500字，建议阅读5分钟
本文介绍了在图对比学习中更为方便的AF-GCL模型。

论文标题：

Augmentation-Free Graph Contrastive Learning

论文链接：

https://arxiv.org/abs/2204.04874

现有的图对比学习（GCL）模型依赖于图的增强，来学习在不同的增强图中保持不变的表示。作者发现，图的增强能够保存图的低频部分，而扰动图的高频部分，因此图对比学习模型往往能在同质图上取得很好的表现，但在高频的异质图中表现欠佳。基于此，作者提出了不需要增强的 AF-GCL 模型，它能够利用图神经网络聚合出的特征直接生成自监督信号，并且对图的同质性依赖程度更低。

设是一个无向图，其中是顶点集，是边集。设顶点的总数为，边的总数为，顶点的标签为，其中，是类的数量。顶点的特征矩阵为，其中是顶点的特征，是输入特征的维数。邻接矩阵为，若则。

我们的目标是自监督地学习一个 GNN 编码器，以顶点特征和图结构作为输入，以顶点的低维表示作为输出，即。这些表示可以用于下游的监督或半监督任务，如节点分类。

我们定义两种图同质性的衡量标准：点同质性（node homophily）和边同质性（edge homophily）。边同质性定义为连接两个同类顶点的边所占的比例：

而边同质性定义为：

它能够衡量所有节点的平均边-标签一致性。它们都在的范围内，越接近代表同质性越强，越接近代表异质性越强。

定义图的拉普拉斯矩阵（Laplacian matrix）为，其中，。对称归一化拉普拉斯矩阵（symmetric normalized Laplacian）定义为，其中，是的第个特征向量，是对应的特征值矩阵。是最小的特征值，是最大的特征值。

亲和矩阵（affinity matrix）可以由拉普拉斯矩阵导出，。的特征值在到之间，常用于设计基于频域的图神经网络，如图卷积网络（GCN）。

对于拉普拉斯矩阵，更小的特征值对应着更低的频率。我们将按照特征值的大小分解到不同的频率带，即分解为，它的特征值在区间内，，表示频域区间的个数。具体地说，，，其中对于，

注意到所有分解后的矩阵之和即为原对称归一化拉普拉斯矩阵，即。

我们将图对比学习中常用的增强方法总结于表 1 中。

我们希望研究在图的增强中，哪些信息是被保留的，哪些信息是被破坏的。如表 1 所示，常用的图增强方法有四种：属性遮挡（attibute masking）、加边（edge edding）、删边（edge dropping）和图扩散（graph diffusion）。

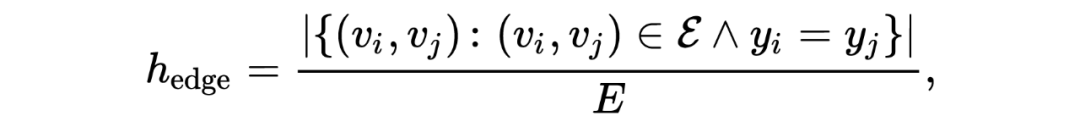
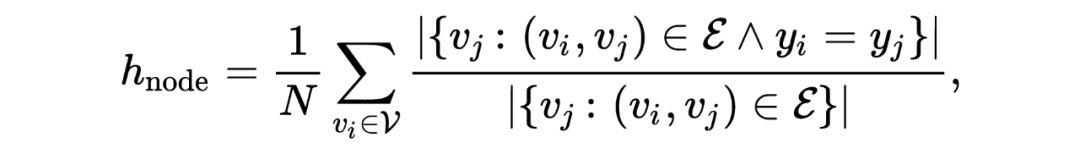
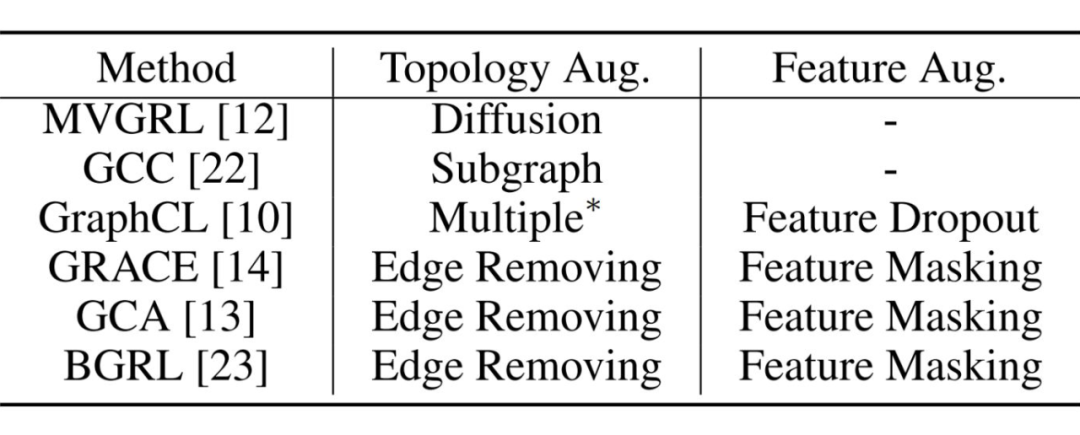
属性遮挡（Attibute Masking）：随机遮挡节点特征的一部分。
加/删边（Edge Adding/Dropping）：随机增/删原始图的一部分边。
图扩散（Graph Diffusion）：基于个性化 PageRank（PPR）的图扩散定义为，其中是扩散系数。

首先我们以删边为例，研究图结构增强的影响。我们将原始图的对称归一化拉普拉斯矩阵的第个部分定义为，将删边后的增强图的对称归一化拉普拉斯矩阵的第个部分定义为。为了研究图增强对不同频率部分的影响，我们用弗罗贝尼乌斯范数（Frobenius norm）作为距离的衡量标准，即。删边对两个同质图数据集（Cora 和 CiteSeer）和两个异质图数据集（Chameleon 和 Squirrel）的影响如图 1 所示。

图1：在 20% 的删边下，原始图和增强图的分解对称归一化拉普拉斯矩阵的弗罗贝尼乌斯距离（Frobenius distance）。实验独立进行 10 次，结果取平均数。

可以看出，图的增强对低频部分影响更小，对中高频部分影响更大。

接着我们以属性遮挡为例，研究特征增强的影响。用表示傅里叶变换（Fourier transform），表示傅里叶逆变换（inverse Fourier transform）。设。我们可以将特征矩阵分解为，其中和分别表示低频和高频部分。于是我们有

其中是一个以为超参数的阈值函数，它将的低频和高频部分分开。由于左边的列对应低频部分，我们将定义为：

进一步地，我们定义属性遮挡后的特征矩阵为，其低频和高频部分分别为。我们通过计算增强前后特征矩阵的弗罗贝尼乌斯距离（Frobenius distance）来研究属性遮挡的影响，并定义为 F-norm-low，为 F-norm-high。结果如表 2 所示。

综上，图的增强会破坏高频信息，而高频信息在下游任务中，尤其是对异质图而言，是非常关键的。因此这导致现有的图对比学习方法在异质图上表现欠佳。

下面我们分析节点特征的集中特性（concentration property），它对于同质图和异质图都是成立的。利用这个特性，我们提出一种不需要增强的图对比学习模型，AF-GCL。

我们假设节点特征服从高斯混合模型（Gaussian mixture model）。简单起见，我们只关注二分类问题。在（二元）标签和一个本征向量下，节点特征可表示为

其中是满足独立标准分布的随机向量，表示本征类。也就是说，以为类的节点的特征服从相同的分布，。进一步地，我们可以对邻居特征做出如下假设。

Assumption 1 对顶点，其邻居的标签独立且服从分布。

该假设表明邻居的标签分布只与中心节点的标签有关，这包括了同质和异质的情况。在该假设下，我们可以证明如下的引理 1，即不论同质还是异质，相同标签节点聚合后的节点特征总是具有相同的嵌入（embedding）。特别地，如图 2 所示，我们对应由 GNN 和 MLP 生成的嵌入为，是对应于输入的嵌入。简单起见，我们引入来表示去掉非线性后等价的 GCN 和 MLP 的线性权重。

▲ 图2：AF-GCL 模型的概述。

Lemma 1 考虑一个满足假设 1 和式（1）的图，其嵌入的数学期望为

进一步地，在至少的概率下，我们有

其中次高斯范数（因为特征的每一维独立同分布），是的最大奇异值。

据此我们可以提出 AF-GCL。如图2，在每个迭代中，首先由编码器生成，再由 L2-正则化的 MLP 生成。在每次迭代中，我们取样个点来组成种子点集（seed node set）；它们的邻居组成节点池（node pool）。对每个种子节点（seed node），其在节点池中最相近的个节点被选为正样本，记为。具体地说就是

由于隐藏表示（hidden representation）是正则化的，隐藏表示的内积就等于余弦相似度（cosine similarity）。目标函数为：

其中节点，和是从它们对应的点集中随机均匀选取的。综上，AF-GCL 的训练算法如算法 1 所示。

Definition 1（Transformed Graph）给定原始图和它的顶点集，其变换图具有相同的顶点集，但它的边由 AF-GCL 选定的正样本顶点对连成，

，如图 3 所示。

图3：由正样本对形成的变换图。

设变换图的邻接矩阵为，边数为，对称归一化拉普拉斯矩阵为。下面的引理 2 表明优化 AF-GCL 的目标函数等价于变换图的矩阵分解（matrix factorization）。

Lemma 2 设矩阵分解的可学习的嵌入为。令。则，矩阵分解的损失函数等价于 AF-GCL 的损失函数，只相差一个常数：

上述引理将优化对比损失函数和矩阵分解联系了起来，我们可以据此给出 AF-GCL 的表现保证。首先分析隐藏表示的内积，。

Theorem 1 考虑一个满足假设 1 和式 (1) 的图。在至少的概率下，我们有

其中，次指数范数

。

由上述定理我们知道隐藏表示的内积以大概率近似于其数学期望。进一步，假设在图的特征和标签分布下，同质性的期望满足，其中

。结合引理 2 和定理 1，我们给出 AF-GCL 理论上的表现保证：

Theorem 2 令

为 GCL 损失函数的最小化函数。存在一个线性分类器，，使得在至少的概率下，

其中是变换图的对称归一化拉普拉斯矩阵的第小的特征值。

上述定理说明，如果变换图的同质性较大，则预测错误的上界会更小。同时，随着隐藏表示的维数的增大，该上界也会变小。

实验部分。实验的具体配置见原论文，这里直接给出结果。在同质图数据集上的实验结果如表 3 所示。

表3：同质图上的图对比学习实验结果。无监督的最优结果用粗体标出。OOM 表示在 32 GB 的 GPU 上内存溢出。

基于图的增强的自监督模型超过了对应的有监督的模型。如前所述，这些增强方法破坏了高频信息，InfoNCE 损失函数使得 GNN 模型保存了低频信息。低频信息的保存让这些对比学习模型在同质图上取得了很好的表现。AF-GCL 在其中 3 个数据集上取得了最优的表现，在其他数据集上也取得了次优的表现。

在异质图数据集上的实验结果如表 4 所示。

表4：异质图上的图对比学习实验结果。无监督的最优结果用粗体标出。OOM 表示在 32 GB 的 GPU 上内存溢出。

与同质图上的实验不同，在大多数数据集上现有的对比学习方法并不能超越一个简单的有监督 GCN。而 AF-GCL 在其中 5 个数据集上都以很大优势取得了最好的表现。在 Twitch-gamers 数据集上，AF-GCL 的表现也不错，毕竟这是 6 个异质图数据集中同质性最高的。对于同质性最低的两个数据集，Chameleon 和 Squirrel，AF-GCL 的表现比其他方法好了很多。这证明了 AF-GCL 模型适合用于异质图。

总结一下，现有的图对比学习方法倾向于保存图的低频信息，打乱图的高频信息，这导致它们在同质图上很成功，但在异质图上并不成功。在对图神经网络聚合特征的理论分析启发下，作者提出了不需要增强的图对比学习模型 AF-GCL，它直接由聚合后的特征生成自监督信号。作者还给出了 AF-GCL 的表现的理论保证。实验中，AF-GCL 在 8 个同质图数据集中的 4 个上都取得了最好的表现，在另外 4 个上也取得了很好的表现；在 6 个异质图数据集中的 5 个上都取得了最好的表现，在另外 1 个上也取得了很好的表现。

编辑：王菁