实信号希尔伯特变换的FPGA实现

0 前言

希尔伯特变换是以德国著名数学家大卫·希尔伯特(David Hilbert，1862年1月23日～1943年2月14日)来命名的。在数学和信号处理中，希尔伯特变换(Hilbert transform)是一个对函数u(t)产生定义域相同的函数H(u)(t)的线性算子。

希尔伯特变换在信号处理中很重要，能够导出信号u(t)的解析表示。这就意味着将实信号u(t)拓展到复平面。希尔伯特变换最初只对周期函数(也就是圆上的函数)有定义，在这种情况下它就是与希尔伯特核的卷积。然而更常见的情况下，对于定义在实直线 R(上半平面的边界)上的函数，希尔伯特变换是指用柯西核做卷积。希尔伯特变换可以与实直线上的函数的傅里叶变换相联系起来的另一种结果[1]。

本文简要介绍了希尔伯特变换，并基于Xilinx FPGA平台，使用最简单的方法实现了实信号的希尔伯特变换。

1 概述

一个实值信号x(t)的希尔伯特变换定义为：

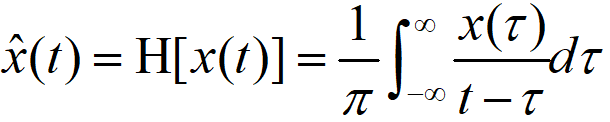
可见一个实值信号x(t)的希尔伯特变换可以看作将x(t)与h(t)=1/(πt)进行卷积。显然它不像傅里叶变换那样从一个域到另一个域，它仍然是由时域到时域的一个变换。这里要注意的是其中的卷积积分表示的其实是该积分的柯西主值，即：

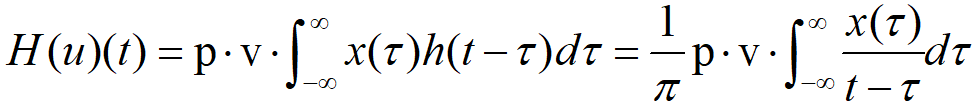
希尔伯特变换之频率响应由傅里叶变换给出：

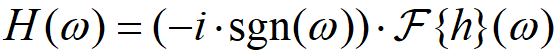
其中有：

𝓕是傅里叶变换，

i(有时写作j)是虚数单位，

ω是角频率，以及：

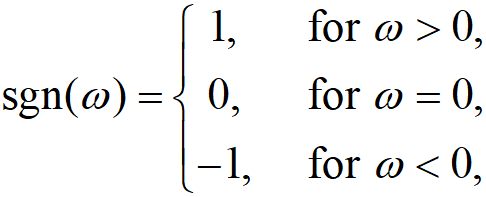
即为符号函数。

以及傅里叶变换：

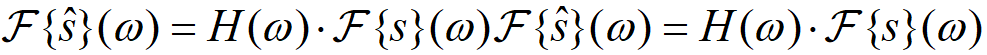
可以看出：希尔伯特变换会将负频率成分偏移+90°，而正频率成分偏移−90°。

2 希尔伯特变换的FPGA实现

希尔伯特滤波器其实是幅度为1(增益为0 dB)的全通滤波器，因此可以用FIR或者IIR滤波器近似实现，通常工程上使用FIR进行逼近。

这部分以250 MSPS采样率的16bit AD采集卡对10 MHz的正弦信号进行采集，并对采集后的信号进行希尔伯特变换，得到一对正交信号。

在MATLAB命令窗口键入“filterDesigner”打开滤波器设计工具的GUI后，左下角设置为如图1所示：

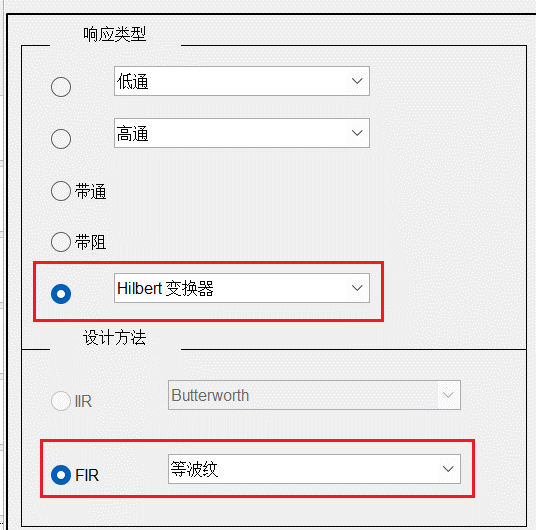
图1：滤波器设置

由于采样率为250 MSPS，因此频率幅值设置如图2所示：

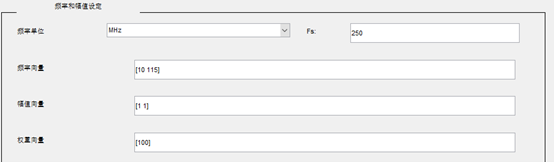
图2：参数设置

根据奈奎斯特采样定理，频率向量中的数值相加应为125，即采样率的一半，例如图2中为10和115。滤波器阶数设置为4n+2(n为正整数)，此处不妨设置为118，即n=29。量化的字长设置为22bit。

得到的希尔伯特变换的幅频响应曲线如图3所示：

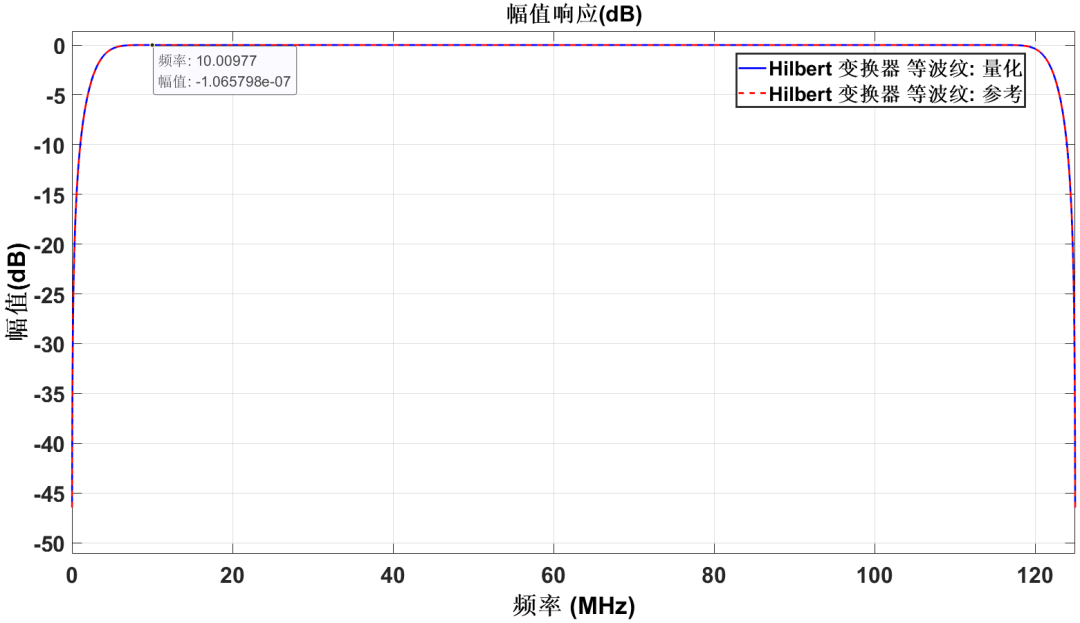
图3：滤波器的幅频响应

由幅频响应曲线可知希尔伯特变换具有滤直流的特性。标记10 MHz附近增益，可以看到该频率点附近的希尔伯特变换的增益很小，不到1.1e-7 dB，几乎为0。通常可以通过增加滤波器阶数或者增大量化字长来进一步减少增益起伏，使其更加接近理想值，此处不做赘述。

完成设计后导出.coe文件，并搭建vivado工程，具体的步骤可以参考傻瓜式教程：FPGA上实现MATLAB filterDesigner设计的FIR低通滤波器。

基于vivado的block design工程及相关IP核设置如图4：

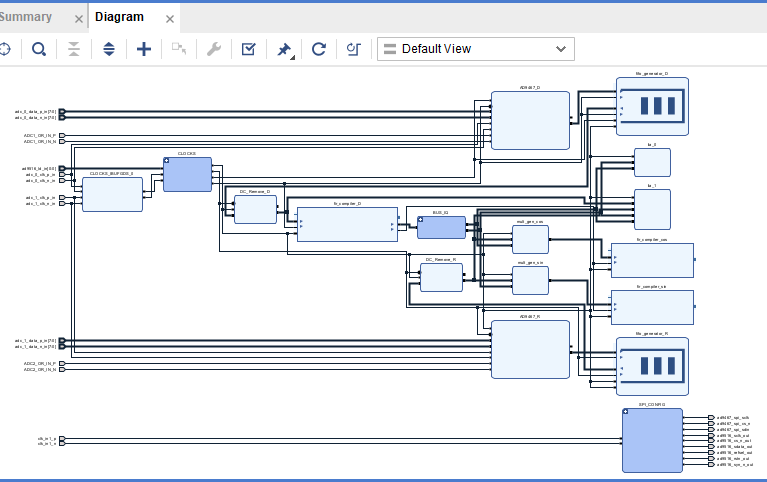
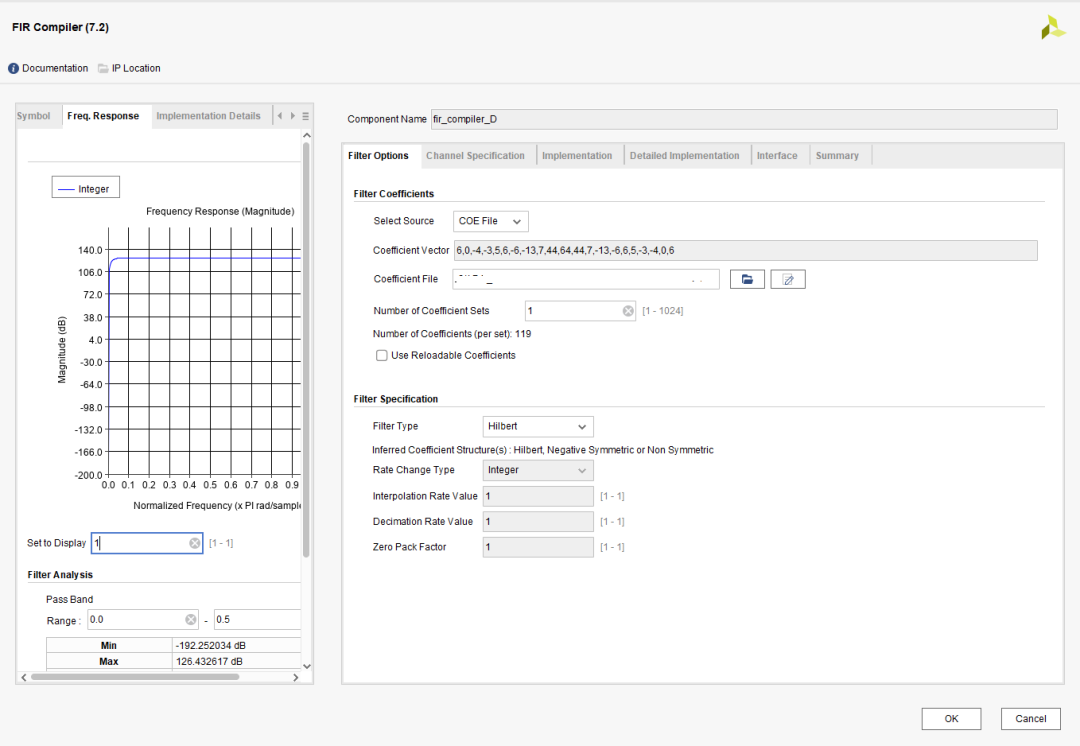
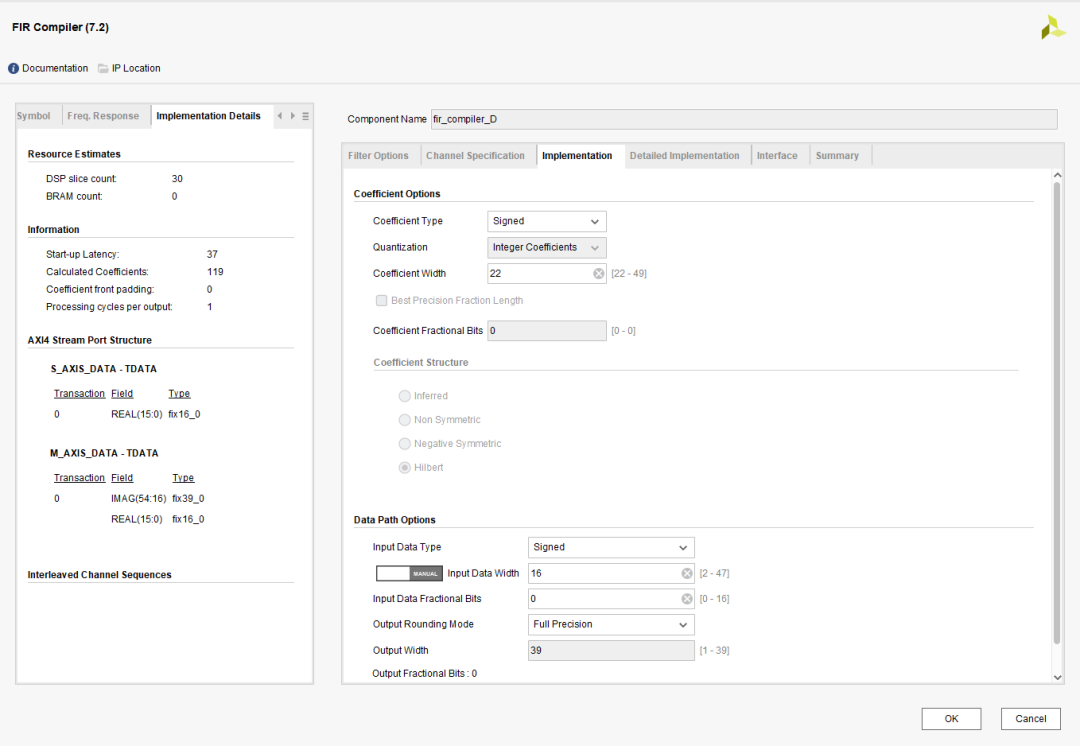
图4：vivado工程及IP核设置

通过ILA抓取的正交信号对如图5：

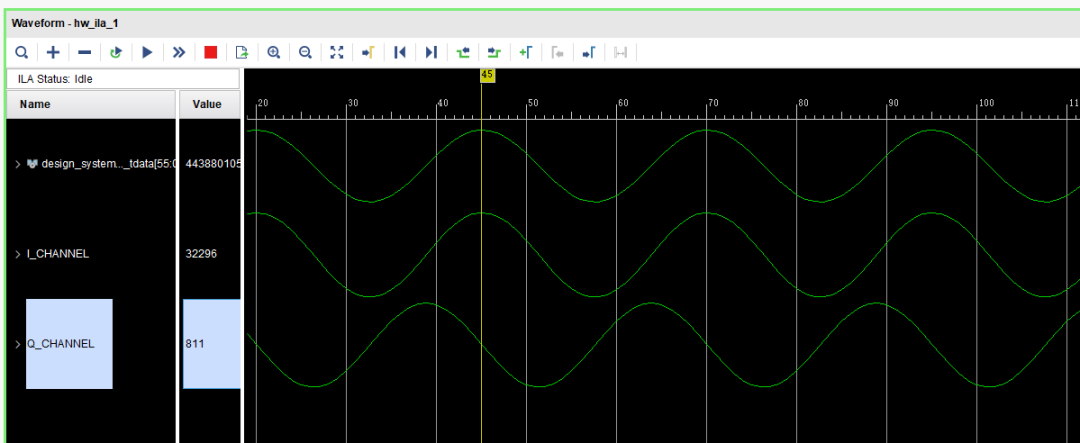
图5：正交信号对

导出的正交信号对数据形成的的李萨茹图如图6所示：

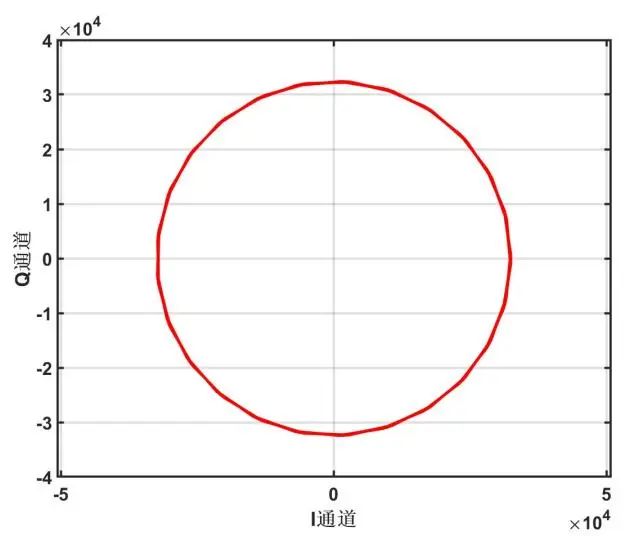
图6：正交信号的李萨茹图

李萨茹图是一个圆心在原点几乎完美的正圆，这表明两路信号完美正交。分别对两通道的信号做FFT，可得到I路信号幅值为31791.2，Q路信号幅值为31790.7，两者幅值几乎相同，相对偏差小于0.008‰，因此两路信号幅值不平衡度几乎可以忽略不计。

3 结论

本文借助MATLAB filterDesigner工具，完成了基于FIR滤波器的希尔伯特变换近似，并在FPGA上实现了对实信号的希尔伯特变换。

4 参考链接

[1]https://en.wikipedia.org/wiki/Hilbert_transform

长按识别二维码关注我们

微信号 ：RPIBMEPhD

写

在

后

面

这是一群致力于科研传播的faculty & PhD记录分享点滴思考的平台，这里有我们在各自领域（机器学习，医疗影像，材料科学，凝聚态物理，生物信息，光学成像等）涉猎研究的点滴感悟，有我们在国内，海外求学工作奋斗的酸甜苦辣，亦有偶尔的风月和我们的诗与远方。

                  ——纯真学者团队