傅立叶变换、拉普拉斯变换、Z 变换的联系是什么?为什么要进行这些变换?
作者丨DBinary@知乎
来源丨https://www.zhihu.com/question/22085329/answer/774074211
编辑丨极市平台




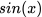
 则表示某一弧度,如果你把这个三角形画在一个二维坐标系的圆上面,比如下面的这种形式
则表示某一弧度,如果你把这个三角形画在一个二维坐标系的圆上面,比如下面的这种形式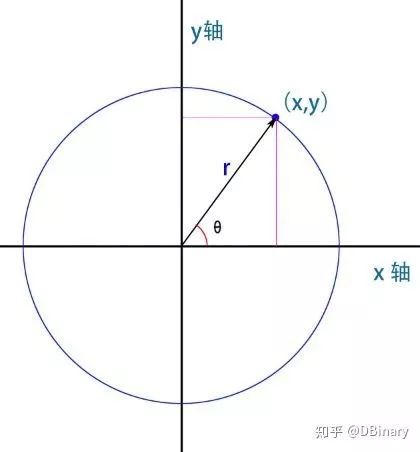
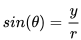 ,当然,这个时候,正弦值还仅仅是一个"正弦值",现在你可以开始想象假如圆上的这个点现在开始动了起来,并开始绕圆逆时针旋转,
,当然,这个时候,正弦值还仅仅是一个"正弦值",现在你可以开始想象假如圆上的这个点现在开始动了起来,并开始绕圆逆时针旋转, 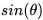 的值会如何变化呢?下面的图会告诉你答案
的值会如何变化呢?下面的图会告诉你答案
这个点围绕的圆到底有多大---->波幅
这个点旋转的速度有多快---->角速度--->频率
这个点最初的位置在哪里---->相位
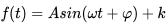
 表示角速度,当然,角速度和频率
表示角速度,当然,角速度和频率 是对应关系,所以信号处理中常常也用角频率这种俗语来描述
是对应关系,所以信号处理中常常也用角频率这种俗语来描述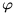 表示相位,sin和cos两个正弦函数的差别其实也仅仅是相位不同
表示相位,sin和cos两个正弦函数的差别其实也仅仅是相位不同 是这个正弦波的偏移,你可以理解为这个波在y轴上如何的上下移动,在信号处理中,这个会被统一到直流分量中(频率为0的波的波幅)
是这个正弦波的偏移,你可以理解为这个波在y轴上如何的上下移动,在信号处理中,这个会被统一到直流分量中(频率为0的波的波幅)
 (式1.0)
(式1.0)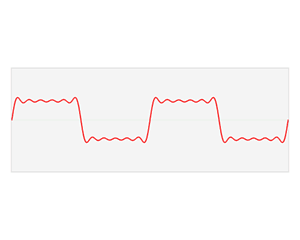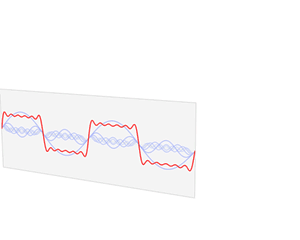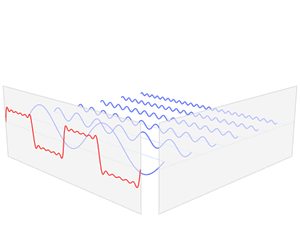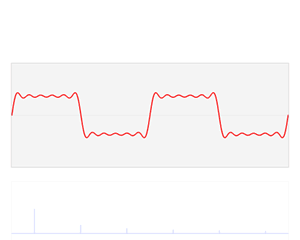
 我们如何把它分解为
我们如何把它分解为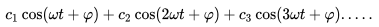

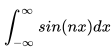 怎么会是0,老师告诉我它明明是发散的,你又忽悠我,关于这点我要说明一下,首先你的老师没说错,不过我也没有忽悠你,首先在大学高数求极限那些知识中,这个函数确实积分后是发散的,这个发散的具体原因是建立在
怎么会是0,老师告诉我它明明是发散的,你又忽悠我,关于这点我要说明一下,首先你的老师没说错,不过我也没有忽悠你,首先在大学高数求极限那些知识中,这个函数确实积分后是发散的,这个发散的具体原因是建立在  这种情况下的,也就是我们正常说的无穷积分,但是如果按这种玩法,基本上大半的信号处理函数都没法玩了,因此在信号处理的公式中比如傅里叶变换,默认都以柯西主值积分作为钦定的积分方式,打个比方定义
这种情况下的,也就是我们正常说的无穷积分,但是如果按这种玩法,基本上大半的信号处理函数都没法玩了,因此在信号处理的公式中比如傅里叶变换,默认都以柯西主值积分作为钦定的积分方式,打个比方定义 这种情况下,负无穷到正无穷的积分不就是0了么,所以这里我说明一下,傅里叶变换中使用的是柯西主值积分,整个无穷区间取周期倍)
这种情况下,负无穷到正无穷的积分不就是0了么,所以这里我说明一下,傅里叶变换中使用的是柯西主值积分,整个无穷区间取周期倍) 和
和 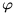 。下面我要甩点公式了,如果感到不适,可以选择跳过
。下面我要甩点公式了,如果感到不适,可以选择跳过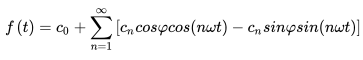
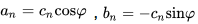 那么,上式变为
那么,上式变为
 用
用 进行检波(说人话就是乘起来,然后为了方便计算对其在一个周期内积分),那么就有
进行检波(说人话就是乘起来,然后为了方便计算对其在一个周期内积分),那么就有
 角频率的正弦波系数为
角频率的正弦波系数为 ,那么根据三角函数的正交性,上式就有
,那么根据三角函数的正交性,上式就有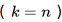 频率一样的情况了么。因此
频率一样的情况了么。因此
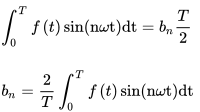
 也可以使用相同的方式进行推导。
也可以使用相同的方式进行推导。 我们可以知道这个波的波幅与相位:
我们可以知道这个波的波幅与相位:
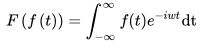
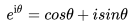

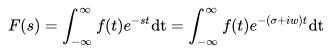
 么,只要搞懂为什么要这么干,我们就能理解拉普拉斯变换了。
么,只要搞懂为什么要这么干,我们就能理解拉普拉斯变换了。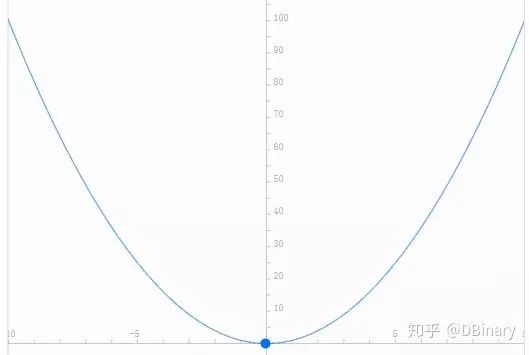
 就行了。
就行了。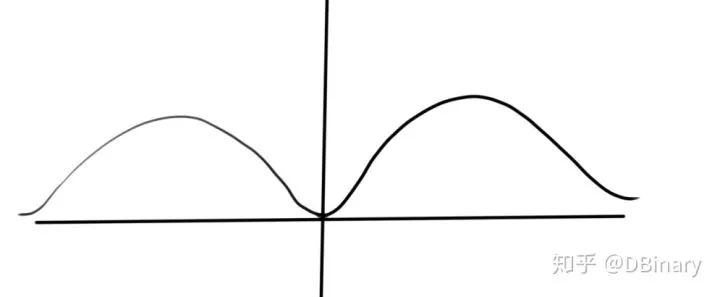
 叫衰减因子
叫衰减因子 ,当然,
,当然, 也是不能用了,这是一个连续信号的写法,而离散的一个一个的点得换成
也是不能用了,这是一个连续信号的写法,而离散的一个一个的点得换成 ,其中的n表示第n个点,实际上就是时间变来的,当然
,其中的n表示第n个点,实际上就是时间变来的,当然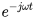 也不能用了,你想啊,我们要具体到某个点,这个点怎么表示,当然了,首先把
也不能用了,你想啊,我们要具体到某个点,这个点怎么表示,当然了,首先把 时间换成
时间换成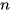 索引号,然后
索引号,然后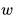 这个动态的角速度值换成具体的角度
这个动态的角速度值换成具体的角度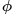 。
。


什么,太简略了不过瘾?
https://zhuanlan.zhihu.com/p/77345128
https://zhuanlan.zhihu.com/p/77347644
https://zhuanlan.zhihu.com/p/77388996
https://zhuanlan.zhihu.com/p/72644228
https://zhuanlan.zhihu.com/p/72644228
https://www.zhihu.com/question/22298352/answer/797335876
来源:极市平台

评论
