基于LeNet5的深度学习FPGA加速实现
点击下方卡片,关注“新机器视觉”公众号
重磅干货,第一时间送达
前文中,我们介绍了一些传统计算机视觉的算法,包括降噪滤波、二值化、缩放、锐化等,最终我们在FPGA上实现了实时的运动目标跟踪算法。近些年基于神经网络的机器学习已经成熟应用于很多商业、工业领域,包括自动驾驶、自动生产,智能医疗等。
那么,作为一本图像处理的入门教材,除了介绍一些传统入门的计算机视觉算法与对应的硬件实现,我们也希望引入最近很流行的神经网络相关的介绍。本章我们将简单介绍卷积神经网络和基于LeNet5实现的手写字符识别,并且在FPGA上实现实时识别的Demo。
1.1.神经网络的介绍
1.1.1.人工神经网络
人工神经网络(Artificial Neural Networks,简称ANN),是受生物神经网络所启发而构建的数学模型,去模拟神经元的动作和神经元之间的联结[1]。一个简单的人工神经网络的计算模型如图1所示。通常一个人工神经网络包含一个输入层,不少于一个的隐藏层和一个输出层。输入层是由一系列的神经元来接受不同的输入;隐藏层是介于输入层和输出层之间的由一层或者多层神经元和连接组成的。通常隐藏层的数量决定了人工神经网络的学习和泛化能力。输出层是输入经由整个神经网络学习和分析得到的高层语义结果,比如目标类型等。
图1(a)所示的人工神经网络也称为感知机(Perception),含有多层隐藏层的人工神经网络为多层感知机(Multi-layer perception)。
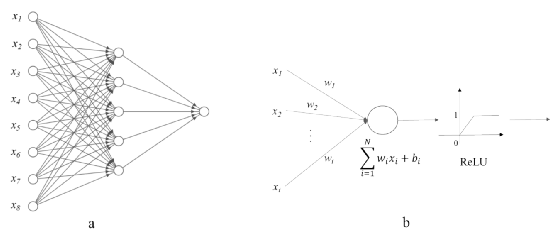
图 1 一个简单人工神经网络的图表展示(a)展示了一个有8个输入神经元,一个隐藏层和一个输出神经元的人工神经网络,(b)展示了在隐藏层中的一个神经元的数学模型,包含累积和激活函数。
如图1(b)所示,隐藏层对所有的输入做加权累积,权重wi反映了不同神经元之间连接的强弱程度,而偏置bi反映了神经元被激活的难易程度。人工神经网络中的激活函数模拟了生物神经网络中神经元的调节器,用来控制神经元的兴奋和静息状态。单个神经元的数学模型hn如下所示:

该公式中,xi是第n个神经元的输入,wni是第i个输入xi对应连接的权重,bn 是第n个的神经元的偏置,φ( )是激活函数,如图1(b)所示,这里用线性整流函数(Rectified Linear Unit)作为激活函数。
1.1.2.卷积神经网络
卷积层是由一系列并行的卷积核(Kernel)组成,通过对输入图像以一定的步长(Stride)进行滑动卷积计算,产生对应的特征图(Feature map),供下一层计算使用。卷积核通常是二维,也有单个点,一维或者三维的。一个典型的卷积核计算公式如下所示:
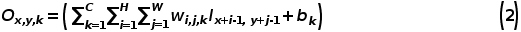
该公式中,Ix,y是第k个卷积核的输入,wi,j,k是第k个输入xx,y对应连接的权重,bk 是第k个卷积核的偏置,x, y分别是输入图像像素点水平和竖直方向上的位置。i,j分别是权重在水平和竖直方向上的索引(Indices)。
池化层是一个在卷积神经网络中常见的操作层,主要有两个作用,一是用来降低维度和计算量。一般卷积计算(步长为1)并不减少维度,而池化层主要是对一定的区域求取最大值或者取均值,这样的操作分别为最大池化(Max pooling)和平均池化(Average pooling),如图2所示,为一个示例展示了平均池化和最大池化分别作用于2×2的区域以2的步长滑动。左边的平均池化是对2 x 2的块内计算平均值,右边的最大池化是对2 x 2的块内寻找最大值。
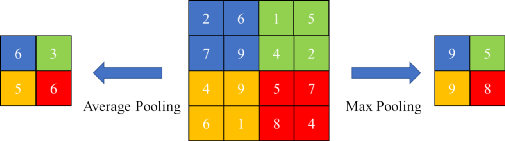
图 2 2×2平均池化与最大值池化
池化层的另一个作用是尽可能多的保存最有效信息。因为经过卷积计算,图像中的物体特征可以被精确地提取出来,但是并非所有的特征都是有效的,池化操作可以保留最有效的信息,同时降低了卷积神经网络对精确特征的敏感度。
批正则化是由Google在2015年提出的[4],目的是为了加速模型收敛,解决内部协变量平移(Internal covariate shift)以及对模型引入正则化。在训练CNN的过程中,由于数据集太大,我们通常只会将一部分数据(mini-batch)放到CPU或者GPU上。批正则化就是对mini-batch的数据都做正则化,转换到均值为0,标准差为1的正态分布。批正则化的具体公式见图3。批正则化的核心思想就是将数据分布变得比较均匀,这样可以稳定梯度,而且让每一层的学习率变化没那么大。CNN的每一层的均值和标准差都是不一样的,这样可以等效为引入一定的噪声,增加了CNN的正则化效果。

图 3 批正则化的具体算法[4]
在人工神经网络中提到的激活函数,是作为一个部件来决定在神经元内的信息通路。从生物学上来说,神经元之间通常由电化学来进行信息传递的。一般神经元会接收到不同来源的电势,如果一个神经元达到了兴奋电势,这个神经元将会产生动作电位,把信息通过神经传递物质或者电势传递给其相邻的神经元。反之,如果一个神经元没有达到兴奋电势,那么它将不能激活也不能传递信息。许多种数学模型用来模拟这个生物特征。S型函数(Sigmoid function)是一个比较常见的激活函数,在人工神经网络和卷积神经网络中使用的比较多,其公式如下:

该公式中,x是激活函数的输入。f(·) 是S型函数,将输出限制在0到1之间(0,1)。S型函数通常用在卷积神经网络的输出层,但是该函数在卷积神经网络优化过程中,有两个问题。第一个是当S型函数的输入趋于无穷大时,在反向传播过程中,梯度会趋近于0,产生了梯度弥散问题,导致卷积神经网络无法正常收敛。第二个问题是S型函数中的指数和除法运算都会消耗比较多的硬件计算资源。前文提到的线性整流函数(ReLU)也是一个在卷积神经网络中常用的激活函数。该函数实现简单,同时又能避免S型函数在反向传播中容易出现梯度消失的问题。它的导数是0或者1,不会消耗较多的计算资源同时也很容易收敛。其公式如下:

在神经网络发展的几十年内,有非常多的理论和应用涌现。本文受限于篇幅,只介绍了基本概念和基础知识。本文只介绍了标准卷积和常用的激活函数,还有很多其他的卷积类型,比如深度卷积(Depthwise convolution),分组卷积(Group convolution),空洞卷积(Dilated convolution),可变性卷积(Deformable convolution)等。激活函数除了S型函数和线性整流函数,还有tanh函数,Leaky ReLU函数,Swish函数等。接下来,笔者会介绍一个基础且经典的卷积神经网络LeNet5,在手写字符识别中的具体应用以及软硬件实现。
1.2.基于LeNet5 CNN的Matlab的实现
1.2.1.LeNet5 CNN简介
LeNet5卷积神经网络最早出现在由Yann LeCun等人于1998年发表在Proceedings of The IEEE学术期刊上的“Graident-based Learning Applied to Document Recognition”这篇文章里[5],用于做手写数字识别(Handwritten digit recognition)。LeNet5卷积神经网络的结构非常简单,如图4所示,其中图中的灰色方块代表了一个特征图。
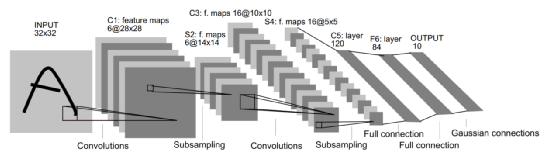
图 4 LeNet5卷积神经网络的架构[5]
LeNet5卷积神经网络有3个卷积层(C1,C3,C5),2个池化层(S2,S4)和2个全连接层(F6和OUTPUT)。LeNet5卷积神经网络的输入是分辨率为32×32的灰度图,所以通道(Channel)数是1。第一层卷积层是由5×5×6的卷积核组成,与输入层进行卷积操作,我们得到28×28×6的特征图,即图4中的C1。经过2×2的平均池化,我们得到14×14×6的特征图,即图4中的S2。然后对S2的特征图进行5×5×16的卷积计算,我们得到10×10×16的特征图,即图4中的C3。后面继续进行池化操作,我们得到5×5×16的特征图,即图4中的S4。最后一层卷积层有5×5×120个卷积核。经卷积计算,我们得到1×1×120的特征图,即图4中的C5。经过两个全连接层,我们最终得到1×1×10的输出,分别对应0-9每个数字的置信度。LeNet5卷积神经网络的结构如表1所示。LeNet5卷积神经网络的参数量大约为60,000左右。
表 1 LeNet5卷积神经网络架构
层 | 通道数 | 滤波器大小 | 步长 | 特征图大小 | 参数量 |
输入层 | 1 | 32×32×1 | |||
卷积层1 | 6 | 5×5 | 1 | 28×28×6 | 5×5×6 + 6 |
池化层1 | 2×2 | 2 | 14×14×6 | ||
卷积层2 | 16 | 5×5 | 1 | 10×10×16 | 5×5×6×16 + 16 |
池化层2 | 2×2 | 2 | 5×5×16 | ||
卷积层3 | 120 | 5×5 | 1 | 1×1×120 | 5×5×16×120 + 120 |
全连接层1 | 84 | 1×1 | 1×1×84 | 1×1×120×84 + 84 | |
全连接层2 | 10 | 1×1 | 1×1×10 | 1×1×84×10 + 10 |
1.2.2.LeNet5 CNN的Matlab实现
首先我们需要准备MNIST的手写数字数据集,从[6]上下载。该数据集中有60,000个训练数据和对应的标签(Label),还有10,000个测试数据和对应的标签。数据集图片和标签的读入格式如下图5,6所示。数据集图片的像素是按照逐行排列的,像素点值是0-255,0代表白色,255代表黑色,标签是0-9。
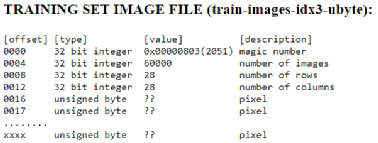
图 5数据集图片读入格式[6]
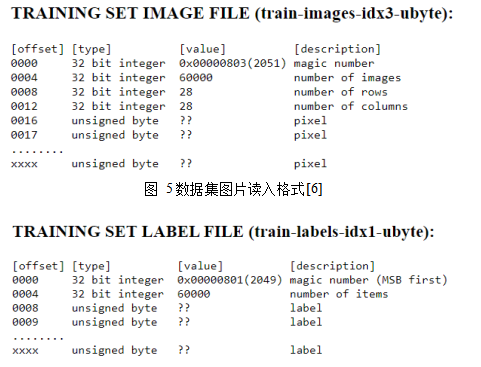
图 6 标签读入格式[6]
在Matlab中,我们将编写读MNIST数据集的函数来准备好训练集和测试集图片及对应的标签。具体代码见loadMNIST.m。


图 7 a)Matlab中读入的手写数字和b)对应的数值
接下来我们将继续构建LeNet5卷积神经网络所需的其他部件,比如卷积层,池化层,激活函数和全连接层。卷积层的输入为H×W×C大小的图像,卷积核为N×Hin×Win×C的一组滤波器,输出为Hout×Wout×N的图像,卷积层还有一个步长参数stride。具体实现代码见Conv2D.m。

对于池化层,没有实现论文中的平均池化,我们这里用最大池化来做,平均池化的实现比较类似,读者有兴趣可以自己实现。池化层的输入为H×W×C大小的特征图,输出为(H/Stride)×(W/Stride)×C大小的特征图,只有一个步长参数。具体实现代码见Maxpool.m。

我们选择用ReLU作为激活函数,方便硬件实现。在Matlab中,我们也利用其向量运算的特性来快速实现ReLU函数,具体代码见ReLU.m。

全连接层就是特殊的卷积层,其卷积核的H和W为1,且输入的H和W为1。所以这里我们复用了Conv2D的代码,不再具体展示了。
现在有非常多好用的平台进行神经网络的训练和部署,笔者参考了Matlab来训练LeNet5卷积神经网络的,就不详述在Matlab上实现LeNet5卷积神经网络的训练过程了(此部分包含误差的计算和反向传递,权值的更新)。有兴趣的读者可以在网上搜索相关的资料进一步理解。这里我们将TensorFlow训练的模型导出,然后在Matlab中读入,对测试集进行推理。如下图8所示,我们将每一层的结果展示出来,方便我们理解LeNet5卷积神经网络的特征提取过程。
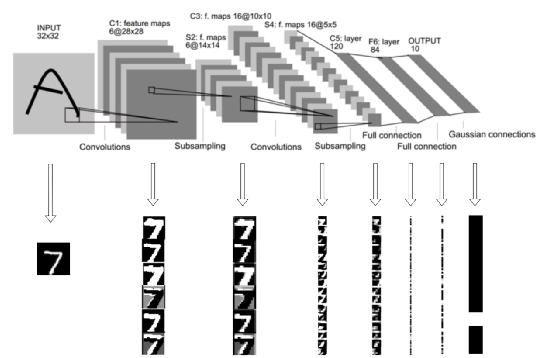
图 8 LeNet5 Matlab实现中对应的每一层特征图
1.3.基于LeNet5 CNN的FPGA硬件加速实现
效果如下,具体的内容,麻烦等书出版吧,谢谢
表 2 LeNet5卷积神经网络的架构和每层所需的内存大小
层 | 通道数 | 滤波器大小 | 步长 | 特征图大小 | 内存大小 |
输入层 | 1 | 32×32×1 | 1024×8 | ||
卷积层1 | 6 | 5×5 | 1 | 28×28×6 | 1024×6×16 |
池化层1 | 2×2 | 2 | 14×14×6 | 256×6×16 | |
卷积层2 | 16 | 5×5 | 1 | 10×10×16 | 128×6×16 |
池化层2 | 2×2 | 2 | 5×5×16 | 32×16×16 | |
卷积层3 | 120 | 5×5 | 1 | 1×1×120 | 128×16 |
全连接层1 | 84 | 1×1 | 1×1×84 | ||
全连接层2 | 10 | 1×1 | 1×1×10 |
图 12 延时优先的LeNet5卷积神经网络的仿真代码结构
图 13 延时优先的LeNet5卷积神经网络的仿真结果
效果如下,具体的内容,麻烦等书出版吧,谢谢
1.4.基于摄像头的字符识别FPGA Demo的搭建与实现
效果如下,具体的内容,麻烦等书出版吧,谢谢
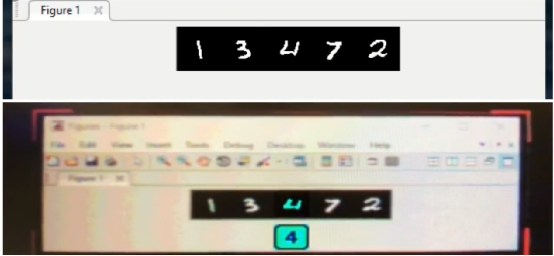
图 16 字符识别的FPGA Demo系统实时识别,手写字符由Matlab生成显示在屏幕上,下面为FPGA Demo的实时识别结果。
本文仅做学术分享,如有侵权,请联系删文。
