拉普拉斯算子的FPGA实现方法
点击下方卡片,关注“新机器视觉”公众号
视觉/图像重磅干货,第一时间送达
引 言
在图像处理系统中常需要对图像进行预处理。由于图像处理的数据量大,对于实时性要求高的系统, 采用软件实现通常难以满足实时性的要求。Altera的QuartusⅡ作为一种可编程逻辑的设计环境,由于其强大的设计能力和直观易用的接口,越来越受 到数字系统设计者的欢迎。QuartusⅡ支持Altera的IP核,包含了LPM/Megafunctions宏功能模块库,设计者只需要选取设置这些 功能模块的相关参数就可以在程序中调用,从而使用户可以充分利用成熟的模块,大大简化了设计的复杂性,加快了设计速度。
拉普拉斯算子是一种重要的图像增强算子,它是一种各向同性滤波器,即滤波器的响应与滤波器作用图像的突变方向无关,而且实现简单,被广泛用于图像锐化和高频增强等算法中。
在此,提出一种使用QuartusⅡ开发环境的Megafunctions功能模块实现拉普拉斯算子的方案,可以做到实时增强图像的高频细节。
1 、Laplacian算子
拉普拉斯算子是各向同性线性算子,二元函数f(x,y)的拉普拉斯变换定义为:
基本高通滤波模板中所有系数的和为0,如果在模板所覆盖的区域内像素的灰度值都相同或者灰度值的变化较为缓慢.则模板的输出为0或输出很小。人们常用的高通提升滤波方法,就是将原图像乘以一个放大因子A,再减去低通滤波图像。高通提升滤波可以表示为:
高通提升滤波图像=A×原图像-低通滤波图像=(A-1)×原图像+原图像-低通滤波图像=(A-1)×原图像+高通滤波图像
即:
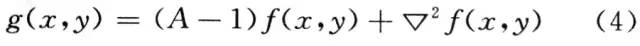
式中:当A=1时,高通提升滤波就是基本的高通滤波;当A>1时,部分原图像被加到高通滤波的结果上,这就恢复了部分高通滤波中丢失的低频成分。因此,经过高通提升滤波的图像与原图像更加相像,同时又对图像的边缘进行了增强。
进行模板卷积的主要步骤为:
(1)将模板在图中漫游,并将模板中心与图中某个像素位置重合;
(2)将模板上系数与模板下对应像素相乘;
(3)将所有乘积相加;
(4)将和(模板的输出响应)赋给图中对应模板中心位置的像素。
当模板遍历图像中的每个像素就得到图像滤波结果。实现Laplacian高通提升滤波的模板如图1所示。
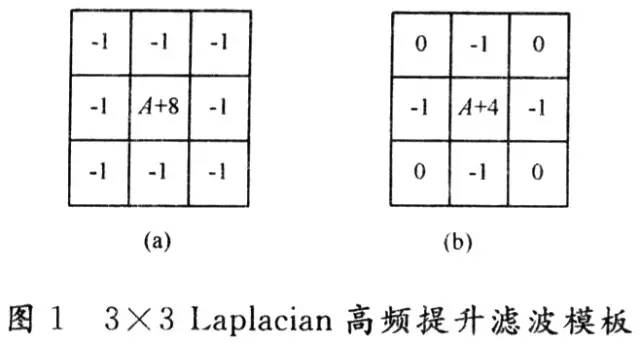
文献[2]的实验证明,使用图1(a)所示掩模能得到更好的锐化效果,所以在硬件实现时使用该掩模。实验中取A=1。
2 、Laplacian算子的硬件实现及结果
使用Laplacian算子滤波是将模板与图像做卷积运算,然后将得到的结果取绝对值后,再进行防治溢出(灰度值大于255)处理。所以在用硬件实现Laplacian算子时可分成三个步骤:构造模板;使用模板对图像进行卷积运算;对卷积后的结果做后处理。
2.1 硬件数据缓存模块
要想得到3×3的方形模板窗,需要使用数据缓存器,在该设计中,调用宏功能模块中的Shift register功能模块就能实现这一功能,十分方便。
Shift register功能模块,是一个可配置的具有抽头(taps)输出的移位寄存器,可实现功能如图2(b)所示。
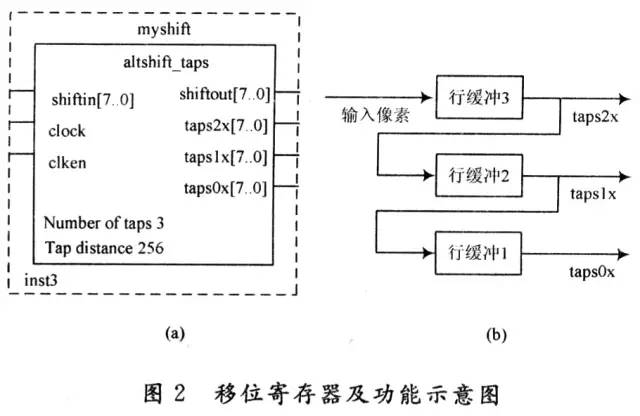
以处理大小为256×256的8位灰度图像为例进行讨论。在对移位寄存器进行配置时,shiftin,shiftout设置为8位,3个抽头。相邻两个抽头相距256。为了方便控制,还需要为该模块添加时钟控制信号,如图2(a)所示。
图2(b)中的行缓冲器分别是由256个8位移位寄存器构成的寄存器链。当图像的第N行数据在像素时钟同步下输入到行缓冲器1后,随着第N+1行图像数据 输入到行缓冲器2中,第N行的图像数据依次存入,而当第N+2行图像数据存入行缓冲器1后,行缓冲器2和行缓冲器3中分别存放的是第N+1行和第N行的图 像数据,从而实现缓冲图像数据的功能。这样在像素时钟的同步下,第N,N+1,N+2行的同一列数据分别从taps0x,taps1x,taps2x端输 出,为构造3×3模块提供了数据准备。
2.2 卷积计算模块
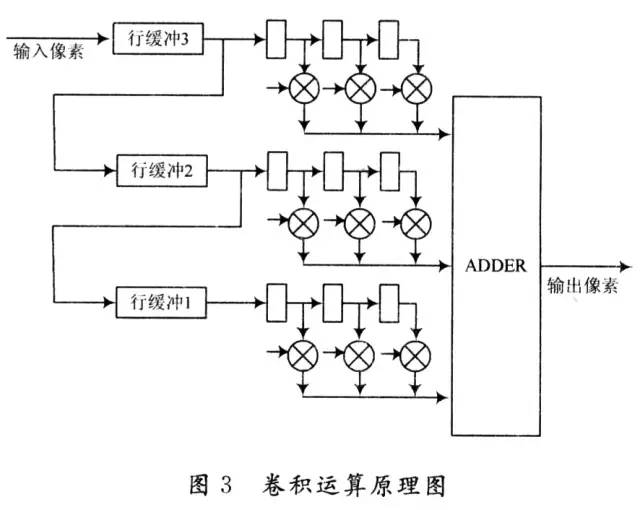
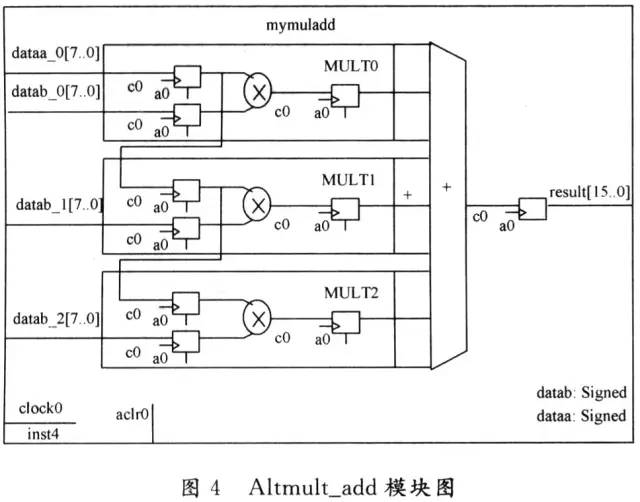
图 3是3×3图像卷积运算的原理图。可以看出,为了实现卷积运算需要做乘法和加法运算,如果直接采用分立的D触发器和加法器以及乘法器来完成卷积运算,结构 会很复杂。在此,采用宏功能模块中的可编程乘加器模块和可编程多路并行加法器模块Parallel_add实现卷积运算,大大简化了设计。
使用可编程多路并行加法器Parallel_add宏功能模块时,可以自由设计输入数据位宽,累加数据个数,定义累加输入数据类型,定义时钟控制端口,增 加异步清零端口等,能快速便捷地生成所需的加法器模块。为了实现卷积运算中的加权和运算,宏功能模块生成的3个乘加器,每个乘加器包含3个乘法器和1个加 法器,如图4所示。图像数据从dataa依次输入,数据分别与固定的模板系数datab_0,datab_1,datab_2相乘。在该实验中,使用 Verilog HDL语言为各datab设值,各值分别对应模板中的权值,并将结果送给加法器完成加法运算。
当采用3个这样类似的Altmult_add模块并联时,便可实现Laplacian算子的运算。
完成图像卷积后需要对结果进行处理,以防止结果出现负值或超过255范围。使用QuartusⅡ提供的Lpm_abs宏功能模块计算绝对值,可以解决出现负值问题,而对超过255的值则均设定为255。
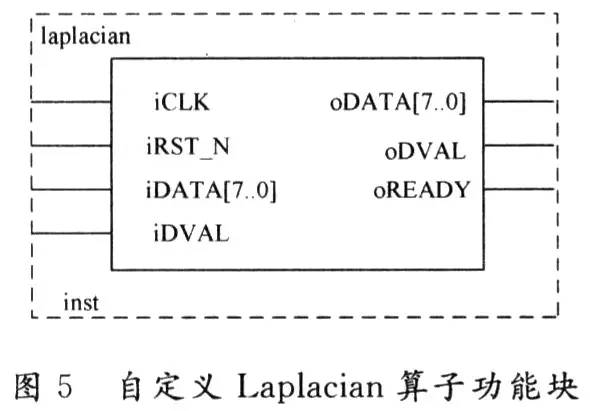
另外,自定义模块如图5所示,将它存于自定义宏功能库中,在以后的设计时,只需修改相关参数即可方便的调用。
2.3 实验结果
图6(a)为一幅256×256的原始图像,(b)为采用Matlab的Laplacian算子进行滤波的结果,(c)为采用本文设计的Laplacian算子得到的结果。比较图6(b)和(c)可以看出,该硬件算法取得了较好的效果。

3 、结 语
这里利用QuartusⅡ软件提供的宏功能模块,通过配置调用的宏功能模块来实现Laplacian算子,该方法既避免了自己编写大量程序代码的繁琐,又 获得较好的实现结果。最后通过与Matlab仿真结果相比较,证明了该设计的有效性。该设计方法方便、快捷,可以推广到其他类型的模板设计中。
