凸优化入门 - 基本概念与 Jensen 不等式
1引言
机器学习中经常会碰到希望优化某个函数值的问题。
例如,给定一个函数
事实上,找到函数的全局最优值在一般情况下可能是一项非常困难的任务。但是,对于一类特殊的优化问题,即凸优化问题,在许多情况下我们可以有效地找到全局最优解。
这意味着我们可以在合理的时间内解决许多实际问题,即从理论上来讲,我们可以在问题规模的多项式复杂度内及时解决问题。
2凸集
.定义
线段 给定两点
的集合,其中
凸集 如果对于
成立,则称集合
直观地讲,这意味着如果我们在
点
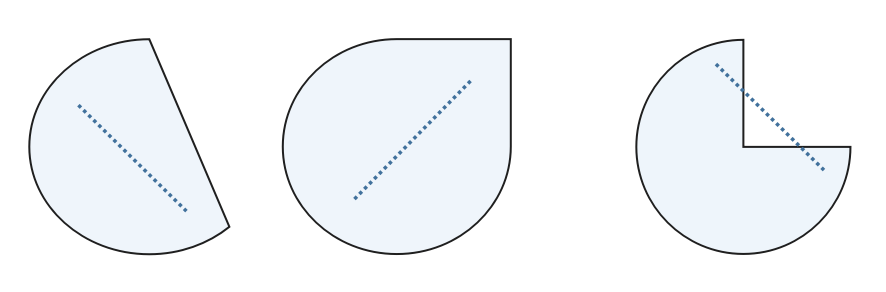
.一些例子
很明显,给定任意
非负象限由
为了验证这是凸集,只需注意给定任意
假设
假设
这里使用了范数定义中的三角形不等式和正齐次性。
给定矩阵
类似地,多面体是(再次可能是空的)集合
为了证明这一点,首先考虑满足
同样,对于满足
类似地,对于两个向量,
假设
仍然是凸集。假设
因此
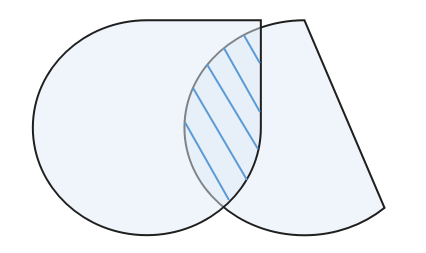
凸集的交集示例
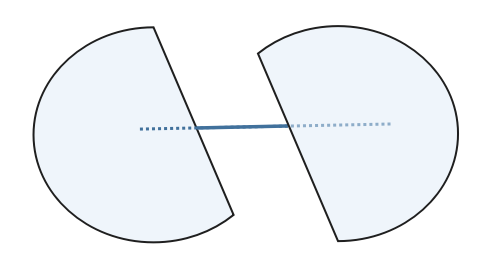
但是请注意,凸集的并集通常不会是凸集。
所有对称半正定矩阵的集合(通常称为半正定锥并表示为
当且仅当
现在考虑两个对称半正定矩阵
相同道理,可以证明所有正定、负定和半负定矩阵的集合也都是凸集。
3凸函数
.定义
凸函数 对于函数
则函数
为了更加形象地理解凸函数,我们画个图看看。假设
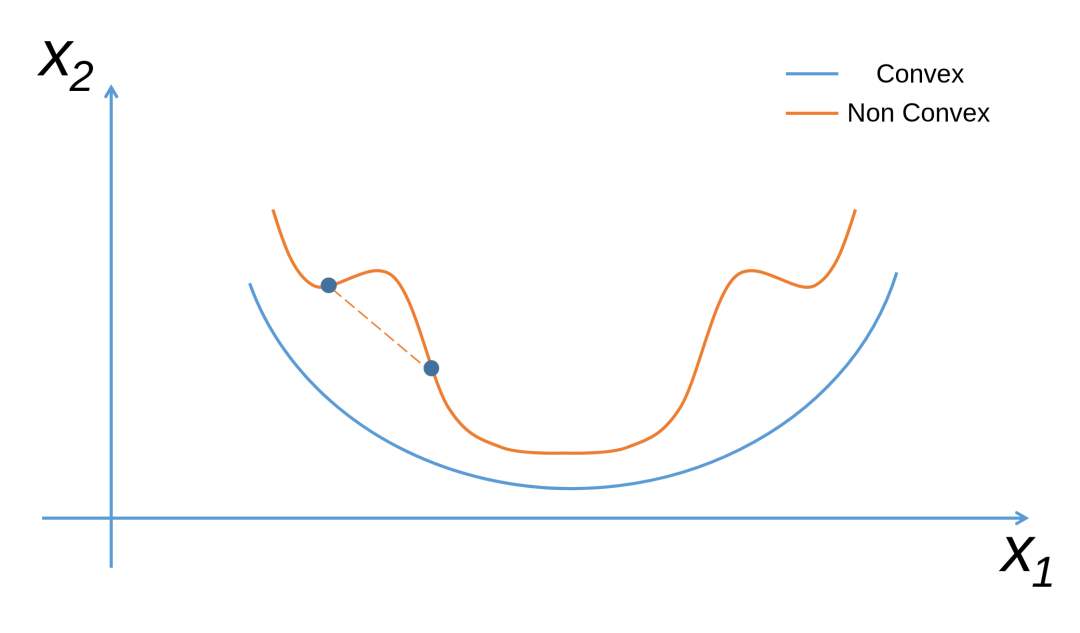
进一步定义,如果上述定义对
注意: 这里要求
请指出下图中哪些是凸函数,哪些不是凸函数。
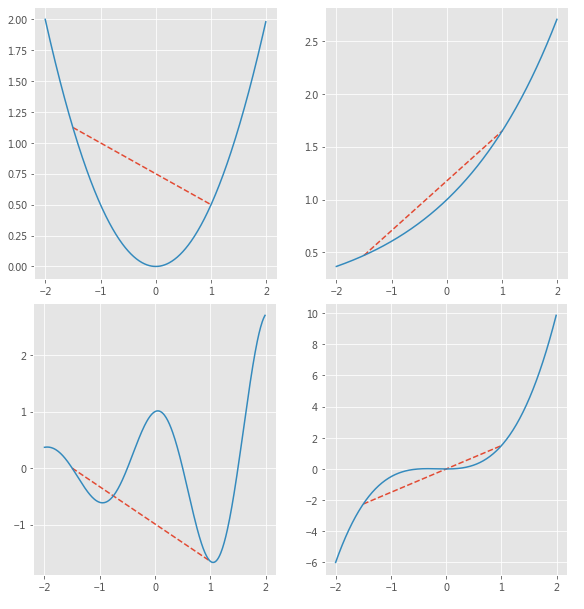
4凸性条件
有了凸函数的定义,那是不是想知道凸函数有些什么特别之处呢?反过来满足什么性质的函数是凸函数呢?
.凸性的一阶条件(First Order Condition for Convexity)
假设函数
都成立的时候,可以称函数
函数
直观地讲,这可以认为是
凸度的一阶条件说,当且仅当切线整体在函数
可以通过下面的图来直观地理解什么是凸性的一阶条件: 对于凸函数上的任一点
.凸性的二阶条件(Second Order Condition for Convexity)
假设函数
此处,该符号
类似于凸性一阶条件的定义,如果
5Jensen 不等式
我们从凸函数的基本定义出发,对于
使用归纳法,可以很容易地将其扩展到多个点的凸组合,对于
实际上,这也可以扩展为无限项之和以及积分。对于积分,当
由于
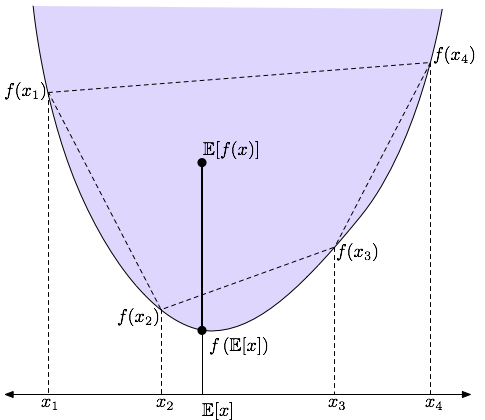
最后这个不等式被称为琴生不等式或者詹森不等式。
可以结合下图来理解上面的不等式。至于这个公式的意义和应用等后面再来揭示哈。
⟳参考资料⟲
Zico Kolter, Honglak. Lee: http://cs229.stanford.edu/section/cs229-cvxopt.pdf.
