SMU激活函数 | 超越ReLU、GELU、Leaky ReLU让ShuffleNetv2提升6.22%


选择一个好的激活函数可以对提高网络性能产生重要的影响。Handcrafted Activation是神经网络模型中最常见的选择。尽管ReLU有一些严重的缺点,但由于其简单性,ReLU成为深度学习中最常见的选择。
本文在已知激活函数Leaky ReLU近似的基础上,提出了一种新的激活函数,称之为Smooth Maximum Unit(SMU)。用SMU替换ReLU,ShuffleNet V2模型在CIFAR100数据集上得到了6.22%的提升。
1介绍
神经网络是深度学习的支柱。激活函数是神经网络的大脑,在深度神经网络的有效性和训练中起着核心作用。ReLU由于其简单性而成为深度学习领域的常用选择。尽管它很简单,但ReLU有一个主要的缺点,即ReLU死亡问题,在这种情况下,多达50%的神经元在网络训练期间死亡。
为了克服ReLU的不足,近年来提出了大量的激活方法,其中Leaky ReLU、Parametric ReLU 、ELU、Softplus、随机化Leaky ReLU是其中的几种,它们在一定程度上改善了ReLU的性能。
Swish是谷歌脑组提出的非线性激活函数,对ReLU有一定的改善;GELU是另一种常用的平滑激活函数。可以看出,Swish和GELU都是ReLU的光滑近似。近年来,人们提出了一些提高ReLU、Swish或GELU性能的非线性激活方法,其中一些是ReLU或Leaky ReLU的光滑逼近方法,还有TanhSoft、EIS、Padé激活单元、正交Padé激活单元、Mish、ErfAct等。
maximum function在原点处是非光滑的。在本文中,作者将探讨maximum function的平滑逼近如何影响网络的训练和性能。
2Smooth Maximum Unit
作者提出了Smooth Maximum Unit (SMU)。从|x|函数的光滑逼近中可以找到一个maximum function的一般逼近公式,它可以平滑逼近一般的maxout族、ReLU、Leaky ReLU或其变体、Swish等。作者还证明了GELU函数是SMU的一个特例。
2.1 平滑近似Maximum Function
Maximum Function定义如下:
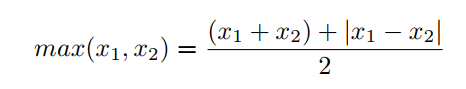
函数|x|在原点是不可微的。因此,从上式可以看出最大值函数在原点处也是不可微的。这里可以用Smooth函数来近似|x|函数。对于本文的其余部分,我们将只考虑两个近似| x, 在深度学习问题中使用这两个函数和近似的结果比其他近似|x|可以得到更好的结果。
注意,从上面平滑地近似|x|,而从下面平滑地近似|x|。这里 是一个平滑参数,当取 时,近似函数平滑地逼近|x|。这里erf是高斯误差函数,定义如下:
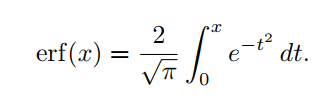
现将式(1)中的|x|函数替换为,则最大函数的光滑逼近公式如下:
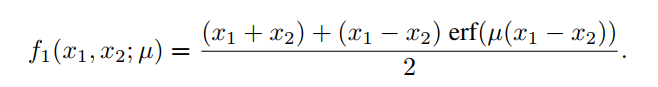
同理,可以推导出的光滑近似公式:
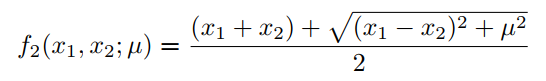
注意,当,;当, 。对于和的特定值,可以近似已知的激活函数。例如,, ,得到:
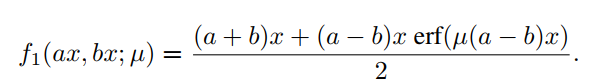
这是maxout族中的一个简单情况,而通过考虑和的非线性选择可以发现更复杂的情况。对于和的特定值,可以得到ReLU和Leaky ReLU的平滑近似。例如,考虑和,有ReLU的平滑近似:
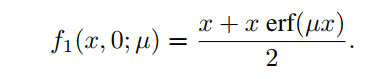
GELU是ReLU的光滑近似。注意,如果方程(5)中取,则可以逼近GELU激活函数,这也表明GELU是ReLU的光滑近似。此外,考虑和,可以得到Leaky ReLU或Parametric ReLU的光滑逼近,这取决于α是超参数还是可学习参数。
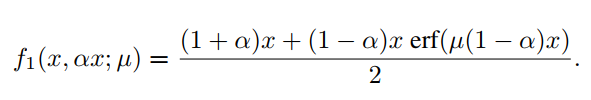
请注意,式(5)和式(6)下端近似为ReLU或Leaky ReLU。同样地,可以从式(3)推导出近似函数,它将近似上面的ReLU或Leaky ReLU。
式(6)对输入变量x的相应导数为:
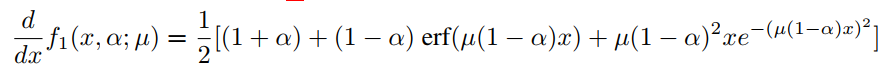
其中,
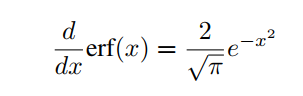
称方程(6)中的函数为Smooth Maximum Unit(SMU)。可以将方程(3)中的和替换为一个函数,称之为SMU-1。对于所有的实验,将使用SMU和SMU-1作为激活函数。
2.2 通过反向传播学习激活参数
使用backpropagation技术更新可训练激活函数参数。作者在Pytorch和Tensorflow-KerasAPI中实现了向前传递,自动区分将更新参数。另外,可以使用CUDA的实现,α和µ参数的梯度可以计算如下:
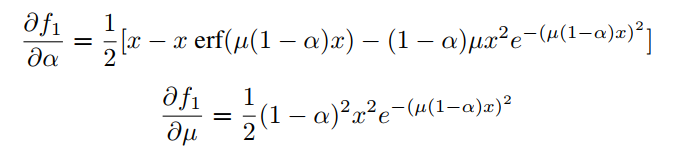
α和µ既可以是超参数,也可以是可训练参数。对于SMU和SMU-1,α = 0.25,这是一个超参数。也将µ作为可训练参数,对SMU和SMU-1分别在1000000和4.352665993287951e−09初始化。
这里,具有SMU和SMU-1激活函数的神经网络密集在C(K)中,其中K是的子集,C(K)是K上所有连续函数的空间。
Proposition
设是任意连续函数。设表示一类具有激活函数ρ的神经网络,在输入层有n个神经元,在输出层有1个神经元,在隐层有任意数目的神经元。设为compact,那么当且仅当ρ是非多项式时C(K)的是dense。
3实验
3.1 分类
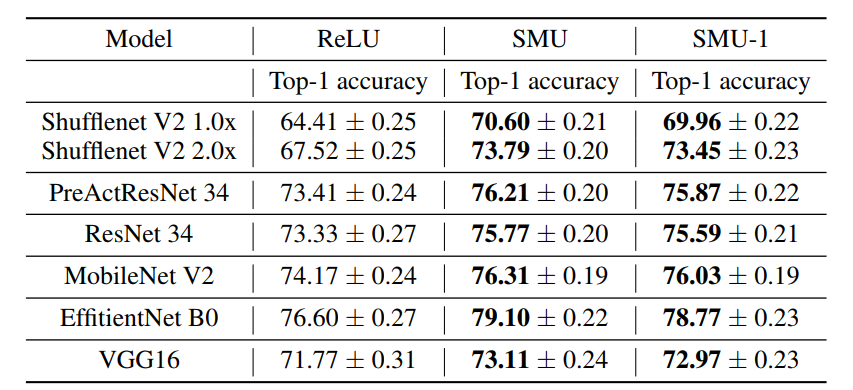
3.2 目标检测
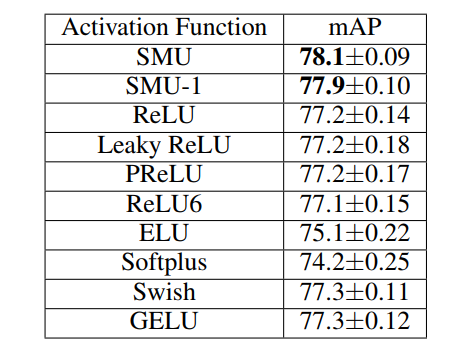
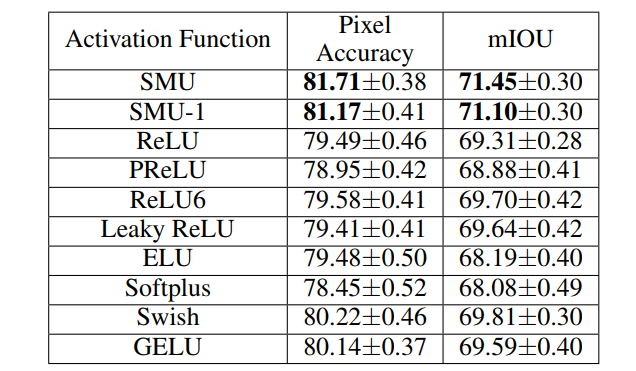
3.3 语义分割
4参考
[1].SMU: SMOOTH ACTIVATION FUNCTION FOR DEEP NETWORKS USING SMOOTHING MAXIMUM TECHNIQUE
5推荐阅读

迟到的 HRViT | Facebook提出多尺度高分辨率ViT,这才是原汁原味的HRNet思想

RMNet推理去除残差结构让ResNet、MobileNet、RepVGG Great Again(必看必看)

α-IoU | 再助YOLOv5登上巅峰,造就IoU Loss大一统
长按扫描下方二维码添加小助手。
可以一起讨论遇到的问题
声明:转载请说明出处
扫描下方二维码关注【集智书童】公众号,获取更多实践项目源码和论文解读,非常期待你我的相遇,让我们以梦为马,砥砺前行!

