八十七、探究最短路问题:Dijkstra算法
「@Author:Runsen」
在上次写道关于数据结构的图,图的算法的考点只有一个:最短路问题。
最短路问题
最短路问题(Shortest Path Problems):给定一个网络,网络的边上有权重,找一条从给定起点到给定终点的路径使路径上的边权重总和最小。
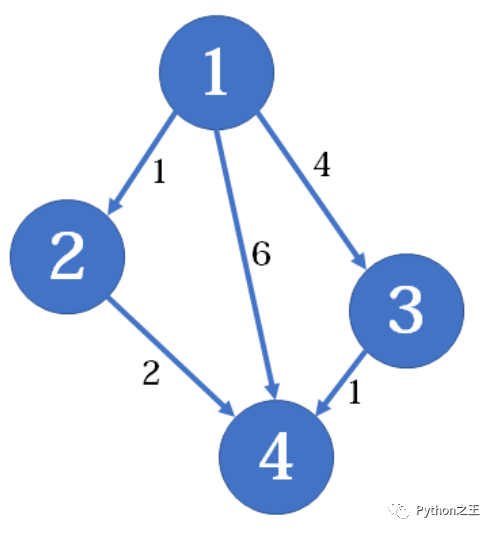
比如上图的:图中点1到点4的最短路径长度应为3(从1到2到4)。
最短路问题常用Dijkstra算法解决
Dijkstra算法
Dijkstra算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
比如,上图Dijkstra算法就是不断地寻找开始节点到邻居节点的所有的路径,将最初的距离设置为最短距离,然后不断的更新节邻居节点的最短距离,直到最远的节点的最短距离求解出来的过程。
文字描述不清楚,看下面的动图。
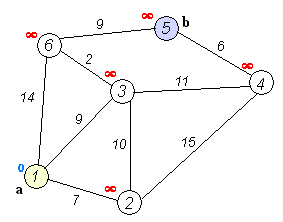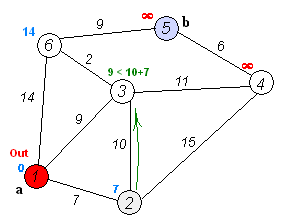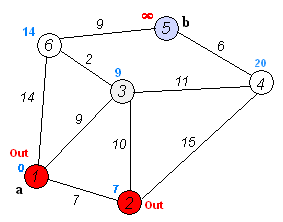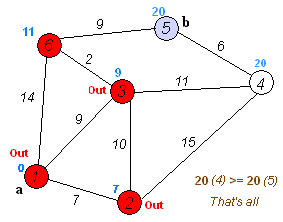
将图上的顶点分为已访问visited和未访问node两个集合。
每次从visited向外拓展一个点,拓展规则是在可更新的点里是距离最小的。
我们还是以上面的图为例

先用邻接矩阵表示无向图:
MAX = 9999
g= [
[0, 1, 4, 6],
[MAX, 0, MAX, 2],
[MAX, MAX, 0, 1],
[MAX, MAX, MAX, 0]
]
邻接矩阵g[0][1]=1表示,第一个节点到第二个节点的距离是1。
目的是要求出开始点1到其他各个点的最小路径距离
n = 4 #4个点
# 初始化 visited
visitd = [0] * (n) #记录该点是否为访问过
# 第一个点已经访问了
visitd[0] = 1
#初始化源点到各个点的距离 node 集合
d = g[0]
for i in range(2, n):
# 遍历d 取出权重最小节点的位置
minWeigth = MAX
for j in range(2, n):
if d[j] < minWeigth and visitd[j] == 0:
minWeigth = d[j]
k = j
# 表示k是当前距1最短的点,同时标记k已经被找过
visitd[k] = 1
# 用该点进行松弛(relax)
for j in range(2, n):
if d[j] > d[k] + g[k][j] and visitd[j] == 0:
d[j] = d[k] + g[k][j]
for i in range(1,n):
print(d[i])
1
4
5
至此,得到节点1到其余三个节点的最短距离是1、4和5。
「把Dijkstra 算法应用于无权图,或者所有边的权都相等的图,Dijkstra 算法等同于BFS搜索。」
多点求解
在很多的时候,要求输入一组点,然后求出输入一个起始点,得到无向图最短路径。
import math
# 假设图中的顶点数
V = 6
# 标记数组:used[v]值为False说明改顶点还没有访问过,在S中,否则在U中!
used = [False for _ in range(V)]
# 距离数组:distance[i]表示从源点s到i的最短距离,distance[s]=0
distance = [float('inf') for _ in range(V)]
# cost[u][v]表示边e=(u,v)的权值,不存在时设为INF
# cost领接表
cost = [[float('inf') for _ in range(V)] for _ in range(V)]
def dijkstra(s):
distance[s] = 0
while True:
# v在这里相当于是一个哨兵,对包含起点s做统一处理!
v = -1
# 从未使用过的顶点中选择一个距离最小的顶点
for u in range(V):
if not used[u] and (v == -1 or distance[u] < distance[v]):
v = u
if v == -1:
# 说明所有顶点都维护到S中了!
break
# 将选定的顶点加入到S中, 同时进行距离更新
used[v] = True
# 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
for u in range(V):
distance[u] = min(distance[u], distance[v] + cost[v][u])
for _ in range(9):
v, u, w = list(map(int, input().split()))
cost[v][u] = w
cost[u][v] = w
s = int(input('请输入一个起始点:'))
dijkstra(s)
print(distance)
测试用例
0 1 1
0 2 2
0 3 3
1 4 7
1 5 9
2 4 4
3 4 5
3 5 6
4 5 8
请输入一个起始点:0
[0, 1, 2, 3, 6, 9]
在测试用例中的0 1 1表示第一个顶点到第二个顶点的距离是1。
Dijkstra算法使用邻接表的时间复杂度是。因此,很多使用堆进行优化或者使用散列表对多余的空间进行优化。
更多的文章
点击下面小程序
- END -
评论

