最短路问题与标号算法(label correcting algorithm)研究(3)

3. Label Correcting Algorithms

本章将围绕Label Correcting Algorithms展开。首先，3.1小节介绍了最短路径最优性条件，这些条件允许我们评估一组距离标签是否达到最优，以及什么时候我们应该结束算法。基于这一最优性条件，3.2-3.5小节介绍了基本的Label Correcting Algorithms用于求解不含有负环的单源最短路径问题。对于多源最短路径问题将在3.6小节进行讨论，3.7小节将对本章内容进行总结。（小编注：限于篇幅原因，本章将分为三期，详细介绍相关算法）

在正式介绍内容之前我们做一下约定：①本文以有向图作为研究对象；②网络中不含有负环；③网络弧长均为整数；④在实现相应算法时以表格3-1为输入文件。

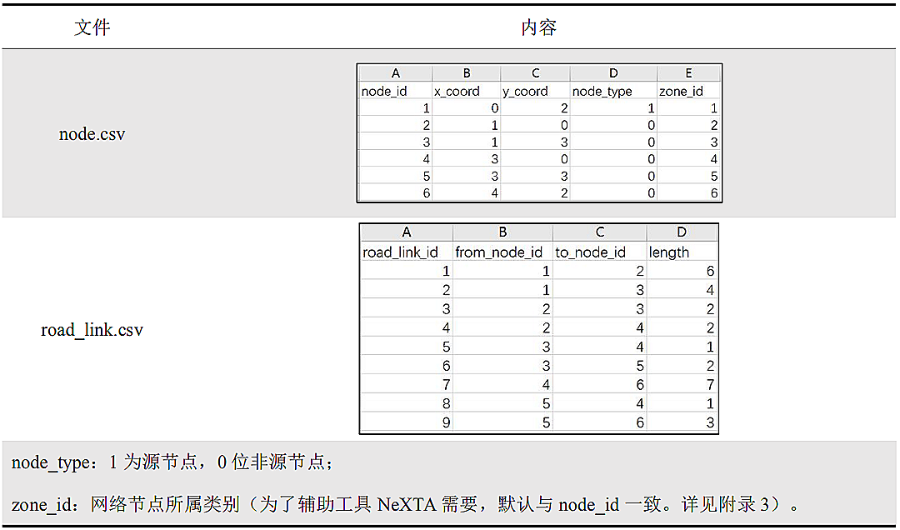
表3-1  算法输入文件格式

最优性定理1

对于任意节点，设表示从源节点到节点的某条有向路径的长度，则当且仅当满足以下最短路径最优性条件时为源节点到节点最短路径距离（3）:

式（3）对于网络中任意弧，源点到节点的最短路径长度始终小于等于源点到节点的最短路径长度与弧的长度之和。反之，如果存在某些弧满足，那么我们就可以把节点加到源节点到节点的路径中去，从而降低源节点到节点的最短路径长度，这与是最短路径长度的命题相矛盾。

接下来我们从数学的角度再次证明上述定理的正确性。假设源点到任意节点的某条有向路径为

由式（3）可得（4）：

把上述不等式相加可得到（5）：

式（5）说明是从源节点到节点的任意有向路径长度的下界，又因为是源节点到节点的临时有向路径长度，因此它又是最短路径的上界，所以即为源节点到节点的最短路径长度。

在此，我们对定理1做进一步拓展：定义表示弧关于距离标签的缩短距离，其计算公式为：关于有以下三条性质：

1.在任意有向环W中，;

2.对于从节点到节点的任意有向路径,;

3.如果是网络中的一条最短路径，则;

接下来思考：如果网络中存在负环，上述三条性质是否还成立？假设W是网络G中的一个有向环，由上述性质3可推出性质1中，因此W不可能是负环。由此得出：含有负环的网络不满足定理1。此外，本文所介绍的最优性判别条件与动态规划中的Bellman Optimality Condition是一致的。

3.2.1 算法介绍

如上文所介绍的最优性判断法则，本文所介绍的Generic Label Correcting Algorithm可以认为是Bellman Optimality Condition的具体实现。在Generic Label Correcting Algorithm中以距离标签来表示源节点到任意节点的最短路径长度，但与Label Setting Algorithms不同的是：这里不区分永久距离标签和临时距离标签，在算法迭代中距离标签是连续变化的，当所有距离标签都满足最优性条件时算法结束，此时距离标签即为源节点到任意节点的最短路径长度。Generic Label Correcting Algorithm步骤如下：

表3-2  Generic Label Correcting Algorithm

我们可以看出Generic Label Correcting Algorithm的伪代码很简洁，核心就是逐个检查不满最优性条件的距离标签，并根据更新距离标签，同时前向节点也随之更新，直到所有的距离标签都满足最优性条件。这里以附录2为例，求解节点1到其他节点的最短路径：

①令节点1的距离标签，前向节点pred(1)=0，其他节点的距离标签设为无穷大，如3-1（a）；②检查弧（1,3），（1,2）是否满足最优性条件，并更新相应距离标签及前向节点，如图3-1（b）；③检查弧（3,4），（3,5）是否满足最优性条件，并更新相应距离标签及前向节点，如图3-1（c）；④检查弧（5,6）,（5,4）是否满足最优性条件，并更新相应距离标签及前向节点，如图3-1（d）。

至此图3-1（d）中的所有弧都满足最优性条件，我们可以通过前向节点集合来生成节点1到其他节点的最短路径，例如，节点5的前向节点为3，节点3的前向节点为1，因此节点1到节点5的最短路径为1-3-5。通过这种方法我们可以得到一颗以节点1为根的前向节点树（如图3-2），此前向节树记录了根节点到其他子节点的最短路径。

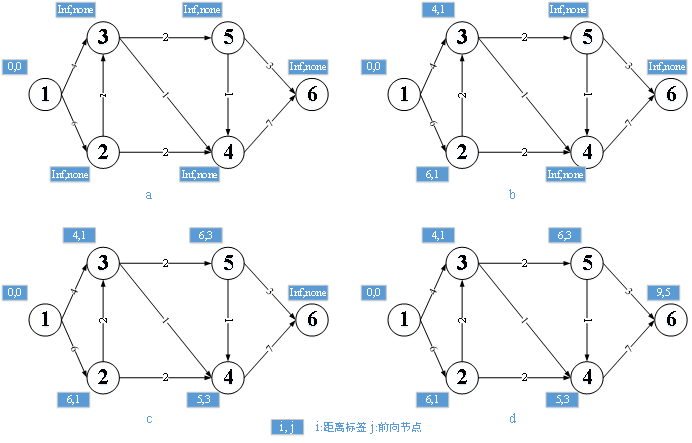图3-1  Generic Label-Correcting Algorithm 计算流程

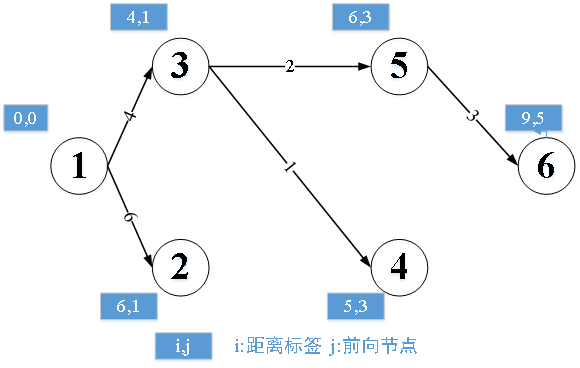图3-2  前向树

这里需要说明的是前向节点集合并不一定会形成一棵以源节点为根的树。如图3-3（a）所示，假设弧（4,1）满足d(1)>d(4)+c41,我们将节点1的前向节点由0更改为4，得到图3-3（b），此时前向节点不再构成一棵树。之所以会发生这种情况是因为网络中含有负环，在3.1小节我们已经讨论过，含有负环的网络不符合最优性定理。

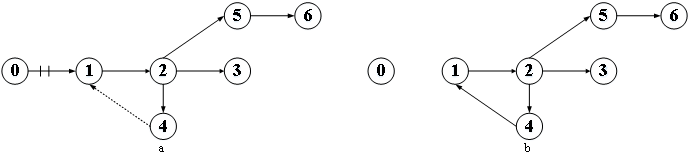图3-3  含有环的前向图

算法复杂度分析

接下来我们对Generic Label Correcting Algorithm的收敛性进行分析。通过伪代码我们得知算法只有一个while循环，但这个循环并没有明确指出迭代次数的值。我们假设为最大的弧长值，那么源节点到其他节点的路径长度上界为（该路径含有n-1条弧，每条弧的长度为），路径长度下界为，所以对于任意距离标签的最大更新次数为（假设每次更新距离标签只减少1单位），网络中节点数目为，因此距离标签总的更新次数为。因为每次迭代只更新一个距离标签，因此总的迭代次数为。

3.2.2 算法实现

首先给出Python版本的Generic Label Correcting Algorithm实现（求解附录2中源节点1到其他节点的最短路径）

"""导入相关基础包，定义全局变量"""
import pandas as pd
import numpy as np
import copy

g_node_list=[] #网络节点集合
g_link_list=[] #网络节点类别集合
g_node_zone={} #网络弧集合
g_shortest_path=[]#最短路径集合
g_origin=None   #网络源节点
g_number_of_nodes=0#网络节点个数
node_predecessor=[]#前向节点集合
node_label_cost=[]#距离标签集合
Max_label_cost=99999#初始距离标签

"""导入网络数据文件，构建基础网络并初始化相关变量"""
#读取网络节点数据
df_node=pd.read_csv('./input_file/node.csv')
df_node=df_node.iloc[:,:].values
for i in range(len(df_node)):
    g_node_list.append(df_node[i,0])
    g_node_zone[df_node[i,0]]=df_node[i,-1]
    g_number_of_nodes+=1
    if df_node[i,3]==1: #第三列node_type数值为1时表示原点
        g_origin=df_node[i,0]
Distance=np.ones((g_number_of_nodes,g_number_of_nodes))*\
Max_label_cost #距离矩阵
node_predecessor=[-1]*g_number_of_nodes
node_label_cost=[Max_label_cost]*g_number_of_nodes
node_predecessor[g_origin-1]=0
node_label_cost[g_origin-1] = 0
#读取网络弧数据
df_link=pd.read_csv('./input_file/road_link.csv')
df_link=df_link.iloc[:,:].values
for i in range(len(df_link)):
    g_link_list.append((df_link[i,1],df_link[i,2]))
    Distance[df_link[i,1]-1,df_link[i,2]-1]=df_link[i,3]

"""最短路径求解：扫描网络弧，依据检查最优性条件更新距离标签"""
while True:
    v=0# 未满足最优性条件的节点个数
    for head,tail in g_link_list:
        if node_label_cost[tail-1]>\
node_label_cost[head-1]+Distance[head-1,tail-1]:
            node_label_cost[tail-1]=\
node_label_cost[head-1]+Distance[head-1,tail-1]
            node_predecessor[tail-1]=head
            v=v+1
    if v==0:
        break
"""依据前向节点生成最短路径"""
agent_id=1
o_zone_id=g_node_zone[g_origin]
for destination in g_node_list:
    if g_origin!=destination:
        d_zone_id=g_node_zone[destination]
        if node_label_cost[destination-1]==Max_label_cost:
            path=" "
            g_shortest_path.append([agent_id, o_zone_id,d_zone_id, path,node_label_cost[destination-1]])
        else:
            to_node=copy.copy(destination)
            path= "%s"%to_node
            while node_predecessor[to_node-1]!=g_origin:
                path="%s;"%node_predecessor[to_node-1]+path
                g=node_predecessor[to_node-1]
                to_node=g
            path="%s;"%g_origin+path
            g_shortest_path.append([agent_id, o_zone_id,d_zone_id,path, node_label_cost[destination - 1]])
        agent_id+=1
"""将求解结果导出到csv文件"""
#将数据转换为DataFrame格式方便导出csv文件
g_shortest_path=np.array(g_shortest_path)
col=['agent_id','o_zone_id','d_zone_id','node_sequence','distance']
file_data = pd.DataFrame(g_shortest_path, index=range(len(g_shortest_path)),columns=col)
file_data.to_csv('./1_generic_label_correcting/agent.csv', index=False)

表3-3  Python实现Generic Label Correcting Algorithm

接下来给出MATLAB版本的Generic Label Correcting Algorithm实现（求解附录2中源节点1到其他节点的最短路径）

%% clear
clc
clear

%% 设置变量
g_node_list = []; %网络节点集合
g_link_list = []; %网络弧集合
g_origin = [];   %网络源节点
g_number_of_nodes = 0;%网络节点个数
node_predecessor = [];%前向节点集合
node_label_cost = [];%距离标签集合
Max_label_cost = inf; %初始距离标签

%% 导入网络数据文件，构建基础网络并初始化相关变量
%读取网络节点数据
df_node = csvread('node.csv',1,0);
g_number_of_nodes = size(df_node,1);
g_node_list = df_node(:,1);
for i = 1 : g_number_of_nodes
    if df_node(i,4)==1
        g_origin=df_node(i,1);
        o_zone_id = df_node(i,5);
    end
end
Distance = ones(g_number_of_nodes,g_number_of_nodes)*Max_label_cost; 
%距离矩阵
node_predecessor = -1*ones(1,g_number_of_nodes);
node_label_cost = Max_label_cost*ones(1,g_number_of_nodes);
node_predecessor(1,g_origin) = 0;
node_label_cost(1,g_origin) = 0;
%读取网络弧数据
df_link = csvread('road_link.csv',1,0);
g_link_list = df_link(:,2:3);
for i = 1 : size(df_link, 1) 
    Distance(df_link(i,2),df_link(i,3)) = df_link(i,4);
end

%% 最短路径求解：扫描网络弧，依据检查最优性条件更新距离标签
while 1
    v=0; %未满足最优性条件的节点个数
    for i = 1 : size(df_link, 1)
        head = g_link_list(i,1);
        tail = g_link_list(i,2);
        if node_label_cost(tail)>…
node_label_cost(head)+Distance(head,tail)
            node_label_cost(tail)=node_label_cost(head)+…
Distance(head,tail);
            node_predecessor(tail)=head;
            v=v+1;
        end
    end
    if v==0
        break;
    end  
end

%% 依据前向节点生成最短路径
distance_column = [];
path_column = {};
o_zone_id_column = o_zone_id * ones(g_number_of_nodes-1, 1);
d_zone_id_column = [];
agent_id_column = [1:(g_number_of_nodes-1)]';
for i = 1: size(g_node_list, 1)
    destination = g_node_list(i);
    if g_origin ~= destination
        d_zone_id_column = [d_zone_id_column; df_node(i,5)];
        if node_label_cost(destination)==Max_label_cost
            path="";
            distance = 99999;
            distance_column = [distance_column; 99999];
        else
            to_node=destination;
            path=num2str(to_node);
            while node_predecessor(to_node)~=g_origin
                path=strcat(';',path);
                path=strcat(num2str(node_predecessor(to_node)),path);
                g=node_predecessor(to_node);
                to_node=g;
            end
            path=strcat(';',path);
            path=strcat(num2str(g_origin),path);
            distance_column = [distance_column; node_label_cost(i)];
        end
        path_column=[path_column;path];
    end
end

title = {'agent_id','o_zone_id','d_zone_id','node_sequence','distance'};
result_table=table(agent_id_column,o_zone_id_column,…
d_zone_id_column,path_column,distance_column,'VariableNames',title);
writetable(result_table, 'agent.csv',…
'Delimiter',',','QuoteStrings',true)

表3-4  MATLAB实现Generic Label Correcting Algorithm

3.3.1 算法介绍

这里先回顾一下Generic Label Correcting Algorithm的核心步骤：对违反最优性条件的弧，更新其对应节点的距离标签及前向节点，即表3-2第4行。我们可以看出在以最优性条件检查距离标签时该算法并没有给出具体的规则，可以认为是一种遍历的方式。因此我们在实现代码时，即表3-3第39行，表3-4第39行，默认采取对所有弧进行遍历。显然这是一个简单但低效的方法。本小节我们将介绍一种改进思路，称其为Modified Label Correcting Algorithm，可有助于提高算法效率。

这里引入一个可扫描列表SE_LIST（Scan Eligible LIST），用来记录可能违反最优性条件的所有弧，如果SE_LIST为空，则表明所有弧都满足最优性条件，已找到最短路径，否则就从SE_LIST中选择一条弧，判定其是否违反最优性条件，并将其从SE_LIST中移除。如果弧违反了最优性条件，就用它更新节点的距离标签，同时更新节点的前向节点。此时请注意，节点的距离标签的任何减少都会影响从节点发出的所有弧的缩减长度，从而导致其中一些弧就可能违反了最优性条件，换句话说，当节点的距离标签更新时，它可能会导致从节点发出的弧不满足最优性条件。还要注意的是，节点的距离标签更新对于所有流入节点的弧都保持最优条件，也就是说节点的距离标签更新不会影响节点的前向节点的最优性。因此，如果节点的距离标签发生改变，则应该将所有从节点发出的弧,即，加入到SE_LIST中。又因为节点唯一对应一个，所以我们可以只记录距离标签发生改变的节点编号，在进行扫描时取出与其对应的，这将有助于减少算法工作量，提高算法效率。以上就是Modified Label Correcting Algorithm的基本思路，其算法步骤如下。

表3-5  Modified Label Correcting Algorithm

算法复杂度分析

在介绍Generic Label Correcting Algorithm的时候我们提到对于任意距离标签最多更新次数为，因此Modified Label Correcting Algorithm总的迭代次数为。当值特别大时，算法总的迭代次数为。

3.3.2 算法实现

首先给出Python版本的Modified Label Correcting Algorithm实现（求解附录2中源节点1到其他节点的最短路径）

"""导入相关基础包，定义全局变量"""
import pandas as pd
import numpy as np
import copy
import random
#全局变量定义
g_node_list=[] #网络节点集合
g_node_zone={} #网络节点类别集合
g_link_list=[] #网络弧集合
g_adjacent_arc_list={}#节点邻接弧集合（从节点i发出的弧集合）
g_shortest_path=[]#OD最短路径集合
g_node_status=[]#网络节点状态
g_origin=None  #网络源节点
g_number_of_nodes=0
node_predecessor=[]#前向节点集合
node_label_cost=[]#距离标签集合
SE_LIST=[]#可扫描节点集合
Max_label_cost=99999#初始距离标签
"""导入网络数据文件，构建基础网络并初始化相关变量"""
#读取网络节点数据
df_node=pd.read_csv('./input_file/node.csv')
df_node=df_node.iloc[:,:].values
for i in range(len(df_node)):
    g_node_list.append(df_node[i,0])
    g_node_zone[df_node[i, 0]] = df_node[i, -1]
    g_number_of_nodes+=1
    g_adjacent_arc_list[df_node[i,0]]=[]
    if df_node[i, 3] == 1:
        g_origin = df_node[i, 0]
g_node_status=[0 for i in range(g_number_of_nodes)] #初始化网络节点状态
Distance=np.ones((g_number_of_nodes,g_number_of_nodes))*\
Max_label_cost #距离矩阵
node_predecessor=[-1]*g_number_of_nodes
node_label_cost=[Max_label_cost]*g_number_of_nodes
node_predecessor[g_origin-1]=0
node_label_cost[g_origin-1] = 0
#读取网络弧数据
df_link=pd.read_csv('./input_file/road_link.csv')
df_link=df_link.iloc[:,:].values
for i in range(len(df_link)):
    g_link_list.append((df_link[i,1],df_link[i,2]))
    Distance[df_link[i,1]-1,df_link[i,2]-1]=df_link[i,3]
    g_adjacent_arc_list[df_link[i,1]].append(df_link[i,2])

"""最短路径求解：扫描网络弧，依据检查最优性条件更新距离标签"""
SE_LIST=[g_origin]
g_node_status[g_origin-1]=1
while len(SE_LIST):
    head=random.sample(SE_LIST,1)[0]#从待检查集合中随机抽取节点
    g_node_status[head-1]=0
    SE_LIST.remove(head)#将被抽取的节点从集合中移除
    adjacent_arc_list=g_adjacent_arc_list[head]#获取当前节点的邻接弧
    for tail in adjacent_arc_list:
        if node_label_cost[tail-1]>\
node_label_cost[head-1]+Distance[head-1,tail-1]:
            node_label_cost[tail-1]=\
node_label_cost[head-1]+Distance[head-1,tail-1]
            node_predecessor[tail-1]=head
            if g_node_status[tail-1]==0:
                SE_LIST.append(tail)
                g_node_status[tail-1]=1
"""依据前向节点生成最短路径"""
agent_id=1
o_zone_id=g_node_zone[g_origin]
for destination in g_node_list:
    if g_origin!=destination:
        d_zone_id=g_node_zone[destination]
        if node_label_cost[destination-1]==Max_label_cost:
            path=" "
            g_shortest_path.append([agent_id, o_zone_id,d_zone_id,path, node_label_cost[destination - 1]])
        else:
            to_node=copy.copy(destination)
            path="%s"%to_node
            while node_predecessor[to_node-1]!=g_origin:
                path="%s;"%node_predecessor[to_node-1]+path
                g=node_predecessor[to_node-1]
                to_node=g
            path="%s;"%g_origin+path
            g_shortest_path.append([agent_id, o_zone_id,d_zone_id,path, node_label_cost[destination - 1]])
        agent_id+=1
"""将求解结果导出到csv文件"""
#将数据转换为DataFrame格式方便导出csv文件
g_shortest_path=np.array(g_shortest_path)
col=['agent_id','o_zone_id','d_zone_id','node_sequence','distance']
file_data = pd.DataFrame(g_shortest_path, index=range(len(g_shortest_path)),columns=col)
file_data.to_csv('./2_modified_label_correcting/agent.csv', index=False)

表3-6  Python实现Modified Label Correcting Algorithm

接下来给出MATLAB版本的Modified Label Correcting Algorithm实现（求解附录2中源节点1到其他节点的最短路径）

%% clear
clc
clear

%% 设置变量
g_node_list = []; %网络节点集合
g_link_list = []; %网络弧集合
g_origin = [];   %网络源节点
g_number_of_nodes = 0;%网络节点个数
node_predecessor = [];%前向节点集合
node_label_cost = [];%距离标签集合
Max_label_cost = inf; %初始距离标签
g_adjacent_arc_list={}; %节点邻接弧集合（从节点i发出的弧集合）
g_node_status=[]; %网络节点状态
SE_LIST=[]; %可扫描节点集合

%% 导入网络数据文件，构建基础网络并初始化相关变量
%读取网络节点数据
df_node = csvread('node.csv',1,0);
g_number_of_nodes = size(df_node,1);
g_node_list = df_node(:,1);
g_node_status=zeros(1,g_number_of_nodes);
for i = 1 : g_number_of_nodes
    if df_node(i,4)==1
        g_origin=df_node(i,1);
        o_zone_id = df_node(i,5);
    end
end
Distance = ones(g_number_of_nodes,g_number_of_nodes)*Max_label_cost; 
%距离矩阵
node_predecessor = -1*ones(1,g_number_of_nodes);
node_label_cost = Max_label_cost*ones(1,g_number_of_nodes);
node_predecessor(1,g_origin) = 0;
node_label_cost(1,g_origin) = 0;
g_adjacent_arc_list = cell(1, g_number_of_nodes);
%读取网络弧数据
df_link = csvread('road_link.csv',1,0);
g_link_list = df_link(:,2:3);
for i = 1 : size(df_link, 1) 
    Distance(df_link(i,2),df_link(i,3)) = df_link(i,4);
    g_adjacent_arc_list{df_link(i,2)} = [g_adjacent_arc_list{df_link(i,2)}, df_link(i,3)];
end

%% 最短路径求解：扫描网络弧，依据检查最优性条件更新距离标签
SE_LIST=[g_origin];
g_node_status(g_origin)=1;
while ~isempty(SE_LIST)
head=SE_LIST(randperm(numel(SE_LIST),1)); 
%从待检查集合中随机抽取节点
    SE_LIST(SE_LIST==head)=[]; %将被抽取的节点从集合中移除
    g_node_status(head)=0;
    adjacent_arc_list = g_adjacent_arc_list(head); %获取当前节点的邻接弧
    adjacent_arc_list = cell2mat(adjacent_arc_list);
    for i = 1 : length(adjacent_arc_list)
        tail = adjacent_arc_list(i);
        if node_label_cost(tail)>…
node_label_cost(head)+Distance(head,tail)
            node_label_cost(tail)=…
node_label_cost(head)+Distance(head,tail);
            node_predecessor(tail)=head;
            if g_node_status(tail)==0
                SE_LIST = [SE_LIST,tail];
                g_node_status(tail) = 1;
            end
        end
    end   
end

%% 依据前向节点生成最短路径
distance_column = [];
path_column = {};
o_zone_id_column = o_zone_id * ones(g_number_of_nodes-1, 1);
d_zone_id_column = [];
agent_id_column = [1:(g_number_of_nodes-1)]';
for i = 1: size(g_node_list, 1)
    destination = g_node_list(i);
    if g_origin ~= destination
        d_zone_id_column = [d_zone_id_column; df_node(i,5)];
        if node_label_cost(destination)==Max_label_cost
            path="";
            distance = 99999;
            distance_column = [distance_column; 99999];
        else
            to_node=destination;
            path=num2str(to_node);
            while node_predecessor(to_node)~=g_origin
                path=strcat(';',path);
                path=strcat(num2str(node_predecessor(to_node)),path);
                g=node_predecessor(to_node);
                to_node=g;
            end
            path=strcat(';',path);
            path=strcat(num2str(g_origin),path);
            distance_column = [distance_column; node_label_cost(i)];
        end
        path_column=[path_column;path];
    end
end

title = {'agent_id','o_zone_id','d_zone_id','node_sequence','distance'};
result_table=table(agent_id_column,o_zone_id_column,…
d_zone_id_column,path_column,distance_column,'VariableNames',title);
writetable(result_table, 'agent.csv',…
'Delimiter',',','QuoteStrings',true)

表3-7  MATLAB实现Modified Label Correcting Algorithm

在公众号内输入【label correcting】不带【】即可下载本文代码资料

周学松教授 是亚利桑那州立大学(ASU)可持续工程与建筑环境学院教授，目前是Transportation Research Part C的副主编，城市轨道交通urbanrail transit 执行主编，Transportation Research Part B的编委。主要研究大规模多模式交通系统优化和仿真算法。

文案&编辑：崔赞扬、李崇楠（北京交通大学）

审稿人：邓发珩、周航、向柯玮（华中科技大学管理学院）

指导老师：周学松（Arizona State University）

如对文中内容有疑问，欢迎交流。（PS：部分资料来自网络）

如有需求，可以联系：

崔赞扬（北京交通大学博士：dr.zanyang@bjtu.edu.cn）

李崇楠（北京交通大学本科：chongnanli1997@hotmail.com）

周学松（Arizona State University Professor：  xzhou74@asu.edu）

邓发珩（华中科技大学本科三年级：  2638512393@qq.com、个人公众号：程序猿声）

周航（华中科技大学本科一年级：zh20010728@126.com）

向柯玮（华中科技大学本科一年级：2562599523@qq.com）

排版：

程欣悦（1293900389@qq.com）