最短路问题与标号算法(label correcting algorithm)研究(2)

最短路问题与标号算法系列推文传送门：
最短路问题与标号算法(label correcting algorithm)研究(1) - 开篇介绍

一、问题描述

在开始介绍最短路问题之前我们先来简单讨论网络流问题（network flow problems）

在我们日常生活中，网络无处不在：为我们提供电力能源的电力网络，为我们提供方便通讯的电话网络，满足我们各种出行需求的交通网络。

在所有这些问题领域，我们都希望某些实体(电力、消费品、一个人或一辆车,一个消息)从一个点到另一个点尽可能需要少的费用以及获取最大的效益。这就是网络流问题的实质。

﹏﹏

﹏

根据不同的研究目的网络流问题可分为：最短路径问题（shortest path problem）、最大流问题（maximum flow problem）、最小费用流问题（minimum cost flow problem）、最小费用最大流问题（minimum cost maximum flow problem）等等

作为网络流问题的研究内容之一，最短路问题主要解决在网络中从一个节点到另一个节点成本最低的路径是什么。
一种最通用的最短路问题可以如此描述：希望在网络中找到一条从源节点（source node）到接收节点（target node）的最小成本路径，这里的最小成本可定义为路径长度、旅行时间、旅行费用等。二、应用领域

二十世纪六十年代，在最短路问题的研究上已经颇有成效，该问题在计算机科学、运筹学等学科的研究中一直是一个热点问题。

最短路问题在现实应用中也相应的代表了最低成本、最短时间问题等。该问题作为网络流学科中的经典问题，以其丰富的适用性，具有广泛的应用领域。

单就交通运输而言，最短路问题就已经有如下重要应用

应用领域	相关文献
车辆路径规划	毕明华. 动态物流中多点多源最佳路径算法研究与实现[D].浙江理工大学,2019.
公共交通换乘方案及线路规划	张妍. 随机环境下的地铁换乘问题两阶段优化模型[D].北京交通大学,2016.牛学勤,王炜.基于最短路搜索的多路径公交客流分配模型研究[J].东南大学学报(自然科学版),2002.马良河,刘信斌,廖大庆.城市公交线路网络图的最短路与乘车路线问题[J].数学的实践与认识,2004.
航空调度	田倩南. 面向航空调度中机场任务指派与受扰航班恢复问题的研究[D].华中科技大学,2018.
供应链管理	郑金忠,陈宏纪,李兴涛,李友虎.基于供应链的航材配送最短路算法[J].物流技术,2004.
铁路运输调度指挥	苗义烽. 突发事件下的列车运行调度模型与算法研究[D].中国铁道科学研究院,2015.Meng, L., & Zhou, X. Simultaneous train rerouting and rescheduling on an N-track network: A model reformulation with network-based cumulative flow variables[J].Transportation Research Part B: Methodological, 2014, 67: 208-234.
交通流量分配	Zhou X , Taylor J , Pratico F . DTALite: A queue-based mesoscopic traffic simulator for fast model evaluation and calibration[J]. Cogent Engineering, 2014.颜佑启,欧阳建湘.最短路—最大流交通分配法[J].中国公路学报,2005.柳伍生,贺剑,李甜甜,谌兰兰.出行策略与行程时间不确定下的公交客流分配方法[J].交通运输系统工程与信息,2018.
行人出行	Shatu F, Yigitcanlar T. Development and validity of a virtual street walkability audit tool for pedestrian route choice analysis—SWATCH[J]. Journal of transport geography, 2018.
物流运输	Mahmoudi M , Zhou X . Finding optimal solutions for vehicle routing problem with pickup and delivery services with time windows: A dynamic programming approach based on state-space-time network representations[J]. 2015.张运河,林柏梁,梁栋,高红艳.优化多式联运问题的一种广义最短路方法研究[J].铁道学报,2006.
随机条件下路径规划	Yang, L., & Zhou, X. (2014). Constraint reformulation and a Lagrangian relaxation-based solution algorithm for a least expected time path problem[J]. Transportation Research Part B: Methodological. 2014..Xing T , Zhou X . Finding the most reliable path with and without link travel time correlation: A Lagrangian substitution based approach[J]. Transportation Research Part B: Methodological, 2011.

三、数学模型

这里给出通用单源最短路径数学模型描述：

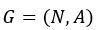G 是由节点集合Ν（元素个数为n）和弧集合A（元素个数为m）组成的网络

定义节点s ∈ N 为源节点（source），其他节点为非源节点（non-source），路径长度为该路径所包含弧的长度之和。求解单源最短路径问题就是找出源节点s到每一个非源节点i的有向最短路径。最短路径问题的数学模型如下：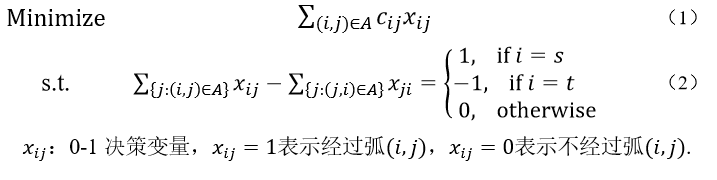

最短路径数学模型

我们可以采用GAMS软件实现上述最短路径模型，并得到准确最优解。这里给出一个GAMS求解Chicago network的简单案例(https://github.com/xzhou99/learning-transportation/tree/master/GAMS_code%20-space-time-network/1%20shortest_path）

GAMS建模过程

variable z;  binary variables  x(a,i,j ) selection of agent a between i and j;
  equations  so_obj  comm_flow_on_node_origin(a,i) origin node flow of agent a on node i at time t  comm_flow_on_node_intermediate(a,i) intermediate node flow of agent a on node i at time t  comm_flow_on_node_destination(a,i) destination node flow of agent a on node i at time t;
  so_obj.. z =e= sum (a,sum((i,j)$(arcs(a,i,j)>0.1), x(a,i,j)*travel_cost(a,i,j)));
  Model SP /ALL/ ;  solve SP using MIP minimizing z;

（左右滑动查看更多）此外，本文所研究的最短路径问题无特殊说明外，均具有以下假设：
● 所有弧长均为整数值● 网络包含从节点s 到网络中所有其他节点的有向路径● 网络不包含负循环● 网络为有向图

四、最短路算法

面对最短路径问题我们可以通过求解整数或线性规划模型（详见：https://en.wikipedia.org/wiki/Unimodular_matrix ）的方法求解，然而这种做法并不高效，当网络含有负环或者网络规模较大时现有计算能力很难对其求解。因此需要更高效的算法来求解最短路径问题。

由于最短路径问题的特殊性，基于图论开发出了许多有效的迭代算法，例如：Dijkstra算法、Floyd-Warshall算法、Bellman-Ford算法等等。表2-3罗列了常见的最短路算法，这些算法被分为两类：Label Setting Algorithm和Label Correcting Algorithm。

表2-3 常见最短路算法分类
这两类算法基本出发点是相同的：在每次迭代时为每个非源节点分配一个临时距离标签，作为源节点到节点,最短路径的估计值。
不同的是它们如何更新临时距离标签：Label Setting Algorithm，在每次迭代时将当前临时距离标签最小的更新为永久距离标签，直到所有的临时距离标签都更新为永久距离标签；
而Label Correcting Algorithm在每次迭代时都有可能更新临时距离标签的值，直到最后一次迭代时所有的临时距离标签才成为永久距离标签。

正因为其更新机制不同，他们所适用的最短路径问题也是有所区别的（如下表）。

Label Setting Algorithms与Label Correcting Algorithms适用条件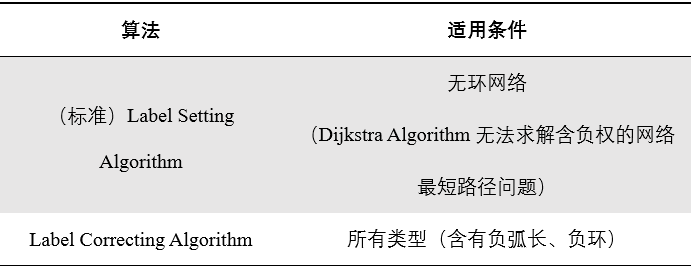

接下来我们以Dijkstra algorithm为例，证明标准Label Setting Algorithm对于含有负环网络的不适用。

Dijkstra algorithm

令为永久距离标签对应的节点集合，非永久距离标签对应的节点集合，为网络节点集合，为网络节点个数，表示源节点到非源节点的临时距离标签，表示非源节点的前向节点，表示从节点发出的所有弧的集合（适用于本文所有符号表示）。

Dijkstra algorithm伪代码如下：

 begin2:      S:="∅"; S ̅:=N;3:      d(i):=∞ for each node i∈N;4:      d(s):=0 and pred(s):=0;5:      while |S| 6:      begin7:         let i ∈S ̅ be a node for which d(i)=min{d(j): j ∈S ̅};8:         S:=S ∪ {i};9:         S ̅:=S ̅– {i};10:         for each arc (i,j)∈A(i) do11:           if d(j) >d(i)+c_ij then d(j):=d(i)+c_ij and pred(j):=i;12:     end;13:   end;

表2-5 Dijkstra Algorithm
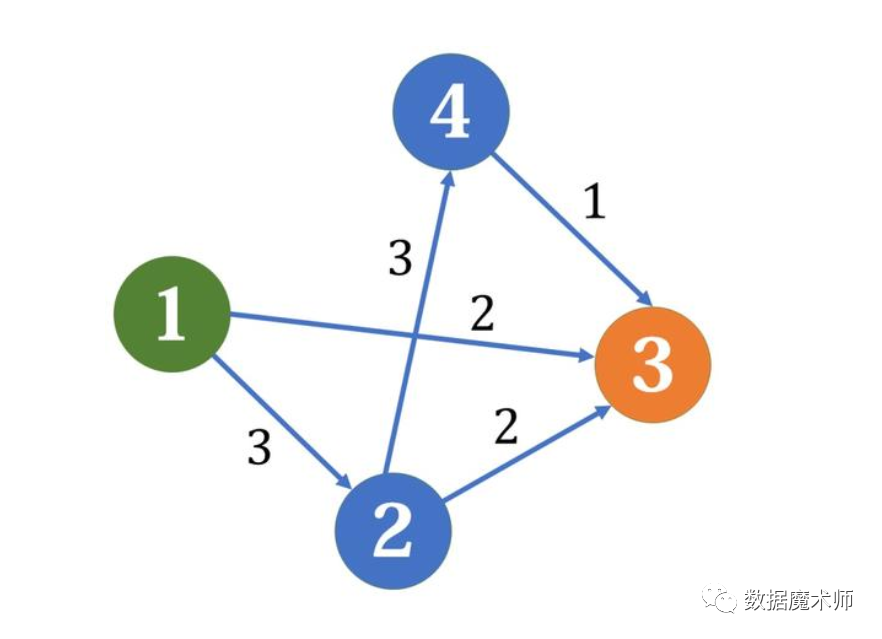
根据表2-5，求解图2-1中从节点1到其他节点最短路径
求解过程

①令,,,,;② 从中选择节点1（距离标签最小）作为当前节点，并将其从移到中（此时节点1标记为永久节点），之后根据判别条件将节点2和3的临时距离标签更新为，前向节点为；③ 继续从中选择节点3（距离标签最小）作为当前节点，并将其从移到中（此时节点3标记为永久节点），之后根据判别条件将节点5的临时距离标签更新为,前向节点为；④ 继续从中选择节点5（距离标签最小）作为当前节点，并将其从移到中（此时节点5标记为永久节点），之后根据判别条件将节点4和6的临时距离标签更新为，前向节点为；⑤继续从中选择节点4作为当前节点，并将其从移到中（此时节点4标记为永久节点），此时没有可更新的距离标签；⑥ 继续从中选择节点2作为当前节点，并将其从移到中（此时节点2标记为永久节点），此时没有可更新的距离标签；⑦ 继续从中选择节点6作为当前节点，并将其从移到中（此时节点6标记为永久节点），此时没有可更新的距离标签，且为空，算法结束。

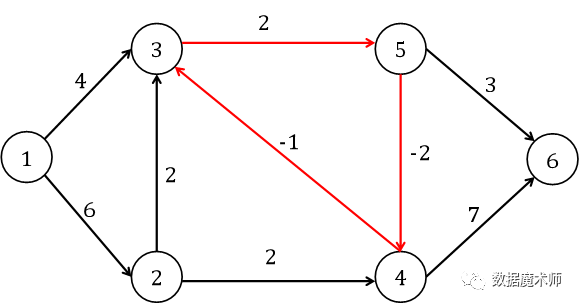图2-1 含有负环的有向图（负环用红色标识）由此得到节点1到其他各节点的最短路径及其长度：1-2（6），1-3（4）,1-3-5-4（4），1-3-5（6），1-3-5-6（9）。

但应注意到节点3、4、5构成一个负环（负环长度为-1），只要经过一次路径长度就减少1，因此可以无限减少节点1到节点3,4,5,6的距离。由此可见，Dijkstra无法正确求解含有负环的网络最短路径问题。其他标准Label Setting Algorithm的情况类似，可自行举出反例进行验证。以上我们通过反例验证标准Label Setting Algorithm不适合处理含负环网络的最短路径问题，Label Correcting Algorithm能否处理这种情况我们将在后续章节进行详细探讨。END

周学松教授是亚利桑那州立大学(ASU)可持续工程与建筑环境学院教授，目前是Transportation Research Part C的副主编，城市轨道交通urbanrail transit 执行主编，Transportation Research Part B的编委。主要研究大规模多模式交通系统优化和仿真算法。

文案&编辑：崔赞扬、李崇楠（北京交通大学）

审稿人：邓发珩、周航、向柯玮（华中科技大学管理学院）

指导老师：周学松（Arizona State University）

如对文中内容有疑问，欢迎交流。（PS：部分资料来自网络）

如有需求，可以联系：

崔赞扬（北京交通大学博士：dr.zanyang@bjtu.edu.cn）

李崇楠（北京交通大学本科：chongnanli1997@hotmail.com）

周学松（Arizona State University Professor： xzhou74@asu.edu）

邓发珩（华中科技大学本科三年级： 2638512393@qq.com、个人公众号：程序猿声）

周航（华中科技大学本科一年级：zh20010728@126.com）

向柯玮（华中科技大学本科一年级：2562599523@qq.com）

推荐阅读：