摘要:群体智能优化算法由于其易实现性及其高效性,已成为最优化方法的研究热点。本文介绍该领域一种近年来的新兴起的优化算法鲸鱼优化算法。在介绍其生物机制的基础上,论述了其捕食、攻击过程的数学模型。最后给出了其与其它优化算法的仿真结果比较。
1. 背景介绍
在流程工业自动化与信息化中,无论操作优化、最优控制,还是生产调度、供应链优化及资源规划等,其实现的理论依据都是最优化方法,因此最优化方法在工业生产起着非常重要的理论基石作用。最优化方法中的启发式优化算法因为它们依赖于相当简单的概念,易于实现,且不需要梯度资料,可以绕过局部最优,可用于涉及不同学科的广泛问题,因此在工程应用中越来越受欢迎。自然启发式优化算法通过模仿生物或物理现象来解决优化问题,又可以分为三大类:基于进化的方法、基于物理的方法和基于群体的方法,本文重点介绍的基于群体智能的优化方法是模仿动物群体社会行为的一种理论。目前该类优化方法包括粒子群算法(PSO)、人工蜂群算法(ABC)、蚁群算法(ACO)、布谷鸟算法(CS)、萤火虫算法等。这类优化算法无论其性质如何,都具有一个共同的特征,即搜索过程分为探索和开发两个阶段。在探索阶段,优化器必须包含操作符来全局探索可搜索空间,移动(即设计变量的扰动)应该尽可能随机化。后续展开的开发阶段,可以定义为对搜索空间中有希望的区域进行详细调查的过程。因此,开发是对在探索阶段发现的设计空间的有希望区域的局部搜索能力。由于优化过程的随机性,如何在探索和开发之间找到合适的平衡点是任何一种启发式算法开发中最具挑战性的任务。本文介绍一种新的模拟座头鲸狩猎行为的群体智能优化算法(鲸鱼优化算法,WOA),采用随机或最佳搜索代理来模拟捕猎行为,并使用螺旋来模拟座头鲸的泡泡网攻击机制。
据研究,鲸鱼大脑的某些区域有与人类相似的梭形细胞,而这些细胞负责人类的判断、情感和社会行为。鲸鱼的这种细胞数量是成年人类的两倍,这是它们聪明的主要原因。事实证明,鲸能像人类一样思考、学习、判断、交流,甚至变得情绪化,但显然它的智能水平要低得多。
据观察,鲸鱼(主要是虎鲸)也能发展自己的方言。而座头鲸最有趣的地方是它们特殊的捕猎方法。这种觅食行为被称为泡泡网觅食法。座头鲸喜欢在接近海面的地方捕食磷虾或小鱼。据观察,这种觅食是通过沿着一个圆圈或“9”形路径创造独特的气泡来完成的,如图1所示。在2011年之前,这一行为仅仅是基于在地表的观察进行研究。后来利用传感器展开了更深入的研究,他们捕获了9头座头鲸的300个标签衍生的泡泡网进食事件。他们发现了两个与气泡有关的动作,并将它们命名为“向上螺旋”和“双环”。在前一种策略中,座头鲸会向下潜水12米,然后开始在猎物周围制造一个螺旋形的气泡,再游向水面。值得一提的是,泡泡网捕食是一种独特的行为,只能在座头鲸身上观察到。本文介绍如何利用螺旋泡沫网捕食机制进行数学建模,以达到优化的目的。
2.2. 数学模型与优化算法
座头鲸能够识别猎物的位置并将其包围。由于优化设计在搜索空间中的位置不是先验已知的,因此WOA算法假设当前的最佳候选解是目标猎物或接近最优解。在定义了最佳搜索个体之后,其他搜索个体将尝试向最佳搜索个体更新它们的位置。这一行为由以下方程表示: (1)
(1)
 (2)
(2)
其中t表示当前迭代, 和
和 是系数向量,X*是目前得到的最佳解的位置向量,
是系数向量,X*是目前得到的最佳解的位置向量, 为位置向量,| |为绝对值,•为逐元素乘法。这里值得一提的是,如果存在更好的解决方案,那么应该在每次迭代中更新X。
为位置向量,| |为绝对值,•为逐元素乘法。这里值得一提的是,如果存在更好的解决方案,那么应该在每次迭代中更新X。
向量 和
和 计算方法如下:
计算方法如下:
 (3)
(3)
 (4)
(4)
这里 在迭代过程中(勘探和开发阶段)从2到0是线性递减的,
在迭代过程中(勘探和开发阶段)从2到0是线性递减的, 是[0,1]中的一个随机向量。
是[0,1]中的一个随机向量。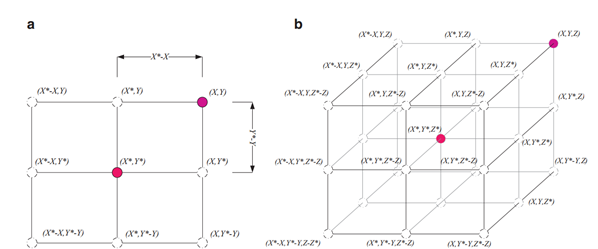
图2 二维和三维位置向量及其可能的下一个位置 (其中X*是目前获得的最佳解决方案)图2(a)结合一个二维问题说明了公式(2)背后的原理。搜索个体的位置(X,Y)可以根据当前最佳记录的位置(X*,Y*)进行更新。围绕最佳个体的不同位置可以通过调整 和
和 向量来得到。图2(b)还描述了搜索在三维空间中可能的更新位置。需要注意的是,通过定义随机向量,可以到达图2所示关键点之间的搜索空间中的任意位置。因此式2允许任何搜索个体更新其在当前最佳解附近的位置,并模拟包围猎物。同样的概念可以扩展到n维的搜索空间,搜索个体将在超立方体中移动,以获得迄今为止最好的解决方案。
向量来得到。图2(b)还描述了搜索在三维空间中可能的更新位置。需要注意的是,通过定义随机向量,可以到达图2所示关键点之间的搜索空间中的任意位置。因此式2允许任何搜索个体更新其在当前最佳解附近的位置,并模拟包围猎物。同样的概念可以扩展到n维的搜索空间,搜索个体将在超立方体中移动,以获得迄今为止最好的解决方案。2)泡泡网攻击方法
为了建立座头鲸泡泡网行为的数学模型,设计了下面两种方法:(1) 收缩包围机制:这种行为是通过减少式(3)中的 来实现,
来实现, 也因此变成(-a, a)之间的一个随机量,a在迭代过程中从2减到0。设置随机值
也因此变成(-a, a)之间的一个随机量,a在迭代过程中从2减到0。设置随机值 在[- 1,1]中,搜索个体的新位置可以定义为介于原个体位置和当前最佳个体位置之间的任何位置。图3(a)显示了在二维空间中0≤a≤1可以实现从(X,Y)变到(X*,Y*)的可能位置。(2) 螺旋更新位置:如图3(b)所示,这种方法首先计算位于(X,Y)的鲸鱼和位于(X,Y,Y)的猎物之间的距离。然后在鲸鱼和猎物的位置之间建立一个螺旋方程,模拟座头鲸的螺旋形运动如式(5):
在[- 1,1]中,搜索个体的新位置可以定义为介于原个体位置和当前最佳个体位置之间的任何位置。图3(a)显示了在二维空间中0≤a≤1可以实现从(X,Y)变到(X*,Y*)的可能位置。(2) 螺旋更新位置:如图3(b)所示,这种方法首先计算位于(X,Y)的鲸鱼和位于(X,Y,Y)的猎物之间的距离。然后在鲸鱼和猎物的位置之间建立一个螺旋方程,模拟座头鲸的螺旋形运动如式(5): (5)这里
(5)这里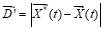 表示第i条鲸到猎物的距离(目前得到的最佳解),b为对数螺旋形状的常数,l为[- 1,1]中的随机数, 是一个元素对元素的乘法。
表示第i条鲸到猎物的距离(目前得到的最佳解),b为对数螺旋形状的常数,l为[- 1,1]中的随机数, 是一个元素对元素的乘法。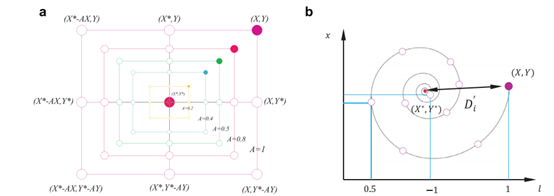
图3 bubbly -net搜索机制在WOA中实现(X是目前获得的最佳解决方案)
座头鲸在一个逐步缩小的圆圈内绕着猎物游动,同时沿着螺旋形的路径游动。为了模拟这种同时发生的行为,我们假设有50%的概率可以在缩小的包围机制和螺旋模型之间做出选择,以更新鲸鱼的位置。模型如下: (6)其中
(6)其中 是一个随机数。座头鲸是根据彼此的位置随机搜索的。随机计算出的
是一个随机数。座头鲸是根据彼此的位置随机搜索的。随机计算出的 比-1小或比1大时,将强迫搜索个体远离参考鲸鱼。相对于开发阶段,我们根据随机选择的搜索个体来更新搜索代理在探索阶段的位置,而不是根据找到的最佳搜索个体,这一机制将使WOA可进行全局搜索。此时的数学模型为:
比-1小或比1大时,将强迫搜索个体远离参考鲸鱼。相对于开发阶段,我们根据随机选择的搜索个体来更新搜索代理在探索阶段的位置,而不是根据找到的最佳搜索个体,这一机制将使WOA可进行全局搜索。此时的数学模型为: (7)
(7) (8)这里
(8)这里 是随机一头鲸对应的随机位置,图4画出了
是随机一头鲸对应的随机位置,图4画出了 时特殊解的一些可能位置。
时特殊解的一些可能位置。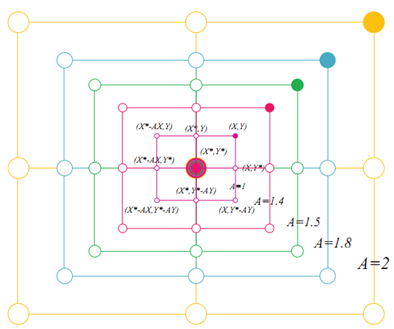
WOA算法从一组随机解开始。在每次迭代中,搜索个体根据随机选择的搜索个体或者获得的最佳解更新其位置,将a参数由2逐步减为为0,以支持勘探和开发。当 时,将选择一个随机的搜索个体;
时,将选择一个随机的搜索个体; 时,将选择最优解作为搜索个体。
时,将选择最优解作为搜索个体。根据p的值,WOA可以在螺旋运动和圆形运动之间进行切换,当满足终止准则时终止WOA算法。
3. 算法的比较效果说明
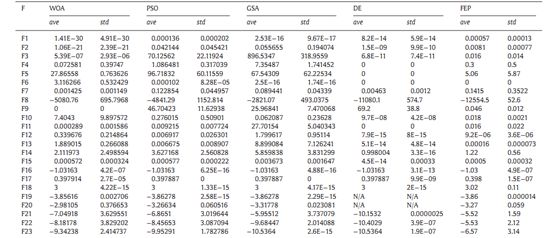
原文中在29个标准测试函数上对该WOA算法进行了测试,结果揭示了所提出的WOA算法的不同特点。WOA具有较高的勘探能力,这是由于式(8)对鲸鱼进行位置更新的机制所致。这个等式要求鲸鱼在迭代的初始步骤中彼此随机移动。而在后续的迭代中,强调高的开发和收敛性,这源于式(6)。这个方程式可以让鲸鱼快速地调整自己的位置,或者沿着螺旋形的路径移动,以获得迄今为止所获得的最佳解。由于这两个阶段是分别完成的,并且几乎在每个迭代的一半中,WOA在迭代过程中同时显示出较高的局部最优避免和收敛速度。然而,PSO和GSA没有操作符来将特定的迭代用于勘探或开发。换句话说,PSO和GSA(以及任何其他类似算法)使用一个公式来更新搜索代理的位置,这增加了局部优化中停滞的可能性。仿真结果见表1和表2。
表1 经典基准函数上的优化结果比较
表2 综合函数上的优化结果比较
为了进一步验证该方法在应用中的性能,原文还对6个结构工程问题(即张力/压缩弹簧的设计、焊接梁的设计、压力容器的设计、15杆桁架的设计、25杆桁架的设计和52杆桁架的设计)和其他优化算法展开了应用比较,最终证实优于传统的优化技术。
参考文献
[1]Mirjalili S, Lewis A. The Whale Optimization Algorithm[J]. Advances inEngineering Software, 2016, Vol. 95, p51-67.
[2]Kaur G , Arora S . Chaotic Whale Optimization Algorithm[J]. Journal ofComputational Design and Engineering, 2018,Vol. 5 (3), p275-284.
[3]Mafarja M M , Mirjalili S . Hybrid Whale Optimization Algorithm with simulatedannealing for feature selection[J]. Neurocomputing, 2017, Vol. 260, p302-312.


(1)
(2)
和
是系数向量,X*是目前得到的最佳解的位置向量,
为位置向量,| |为绝对值,•为逐元素乘法。这里值得一提的是,如果存在更好的解决方案,那么应该在每次迭代中更新X。
和
计算方法如下:
(3)
(4)

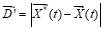 表示第i条鲸到猎物的距离(目前得到的最佳解),b为对数螺旋形状的常数,l为[- 1,1]中的随机数, 是一个元素对元素的乘法。
表示第i条鲸到猎物的距离(目前得到的最佳解),b为对数螺旋形状的常数,l为[- 1,1]中的随机数, 是一个元素对元素的乘法。