SVM 和最优化
点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达
本文转自:机器学习算法那些事
讲解支持向量机(SVM)的文章数不胜数,不过大多缺乏中间很多推导细节。
相比其他经典机器学习算法,SVM里面有更多的数学推导,用到拉格朗日乘子法,KKT条件,线性和非线性的核函数,这些都对非数学专业的入门者造成一定门槛。
不过挑战意味着机遇,完全打通这些知识,可能会助你提升一个台阶,尽管当下SVM用的可能没有之前火爆,但SVM作为在深度学习模型之前应用最广泛的模型之一,仍然有必要研究推导,尤其是如果想继续深造,读博、做科研的。
这篇文章是我之前写的SVM数学推导部分,用的方法比较直白,自信这个推导方法大家都能看明白。
SVM 直接从目标函数和约束部分开始。
SVM经过拉格朗日乘子法,引入了 m 个系数,目标函数的形式如下:
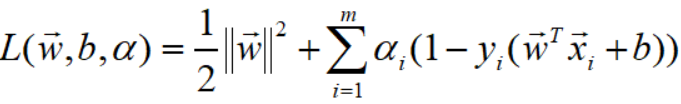
变量含义和相关假设如下:
设 w 向量维度是 m,
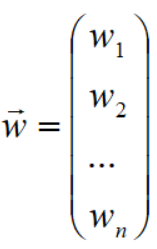
a 的维度是 m (特征个数),
样本(X,Y)的第一维度代表样本个数,设为n; 第二维度是特征维度m,如第 i 个样本的向量表示为:
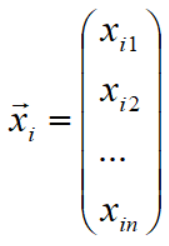
b是标量
因此,下式可以化简为:
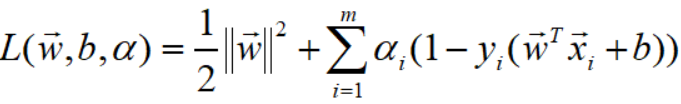
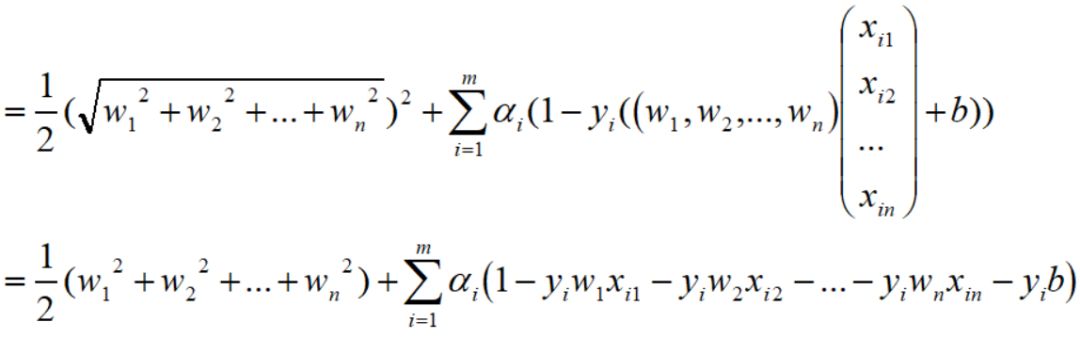
为了更好地理解,
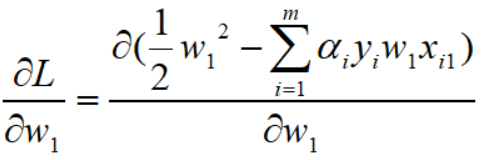
这些只涉及到最简单的求导公式,求出偏导:
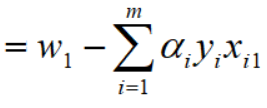
这样对w1的求导完毕,然后对整个的 w 向量求导:
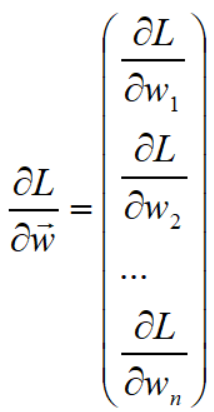
已经求得L对w1的偏导,
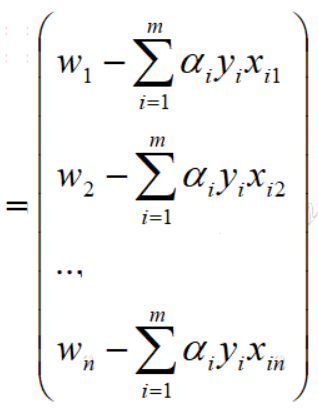
下面再利用一些基本的线性代数中行列式的一些知识,就可以转化为向量的表达,具体操作如下:
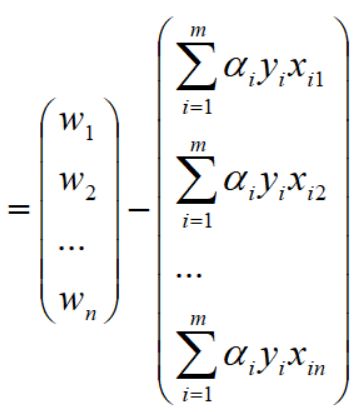
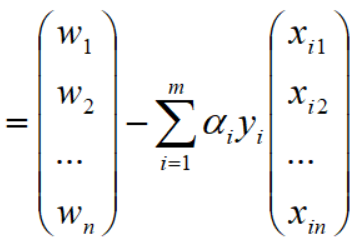
回到文章开始对w向量和xi向量的定义,得到如下向量表达:
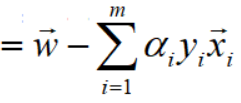
因此,对w向量的偏导求解完毕,结果如下:
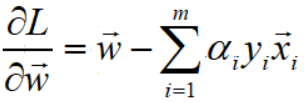
下面
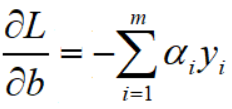
根据拉格朗日乘子法的理论,令L对w偏导等于0,得到关系式:
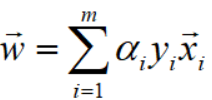
同理,令L对b偏导等于0,得到关系式:
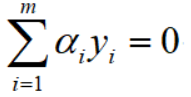
接下来,将得到2个关系式代入到L中,化简L.
为了更好理解,仍然采用更直观地表达方式,将向量完全展开,
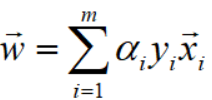
将上面关系式代入到L之前,我们先展开这个式子,

仍然还是先抽出w的第一个分量w1,因为L完全展开中涉及到其平方,
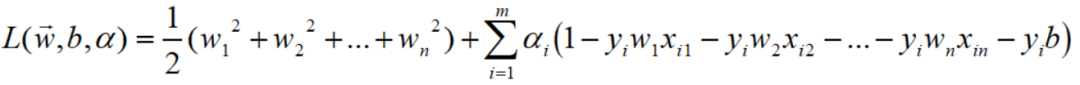
所以,
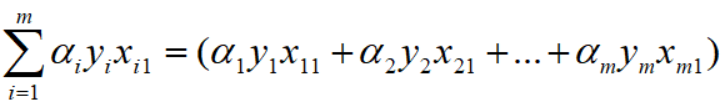
w1的平方,因此可以展成如下形式:
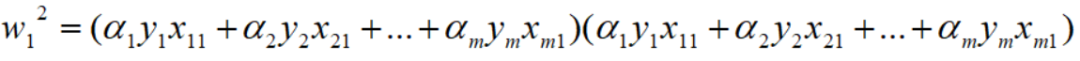
上面这个式子就是基本的多项式求和,w1的平方进一步浓缩下:

至此,w1的平法化简完毕,再整合所有其他w分量并求和,如下,整个推导过程依然相清晰,如下:
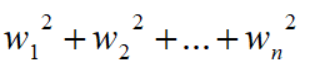
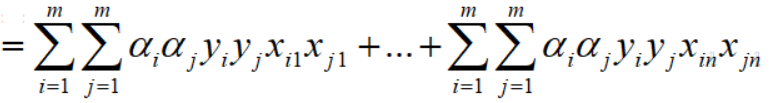
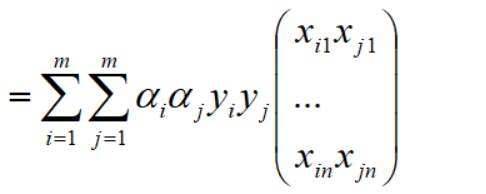
再对上式拆分成两个向量,如下:
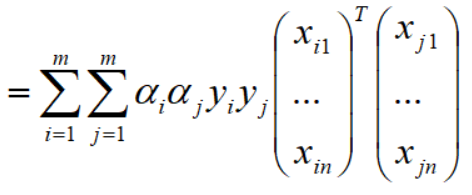
再写成浓缩式子:
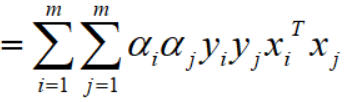
至此,代入w后化简中的第一项已经完毕。
再化简第二块:
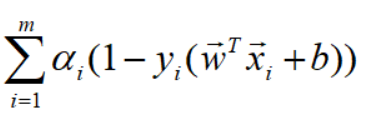
对上式展开,并利用条件: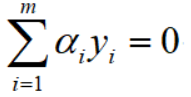 ,化简如下:
,化简如下:
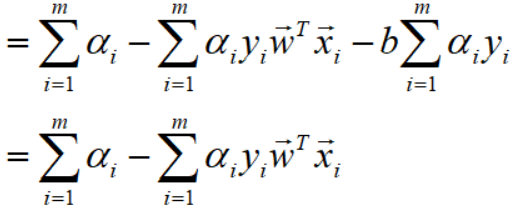
代入w满足的等式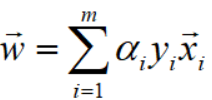 后,
后,
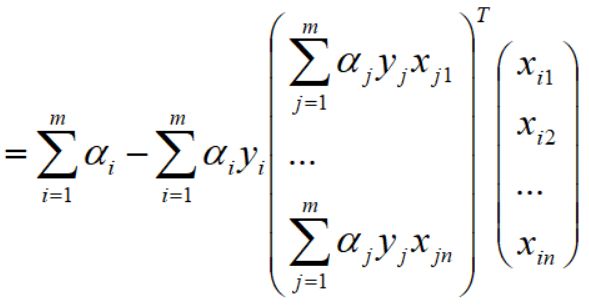
提取出公因子后变为如下:
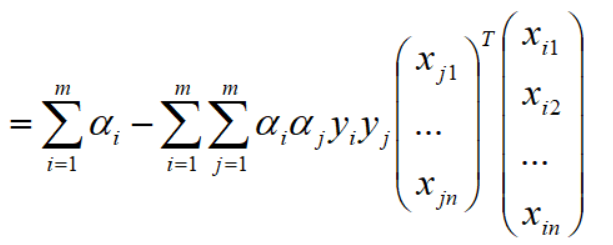
将上式写为向量形式:
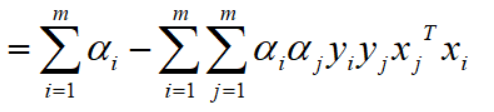
因为都是向量,所以转置相等,故,
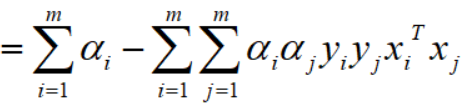
至此,第一二项求解完毕,整理后得到:
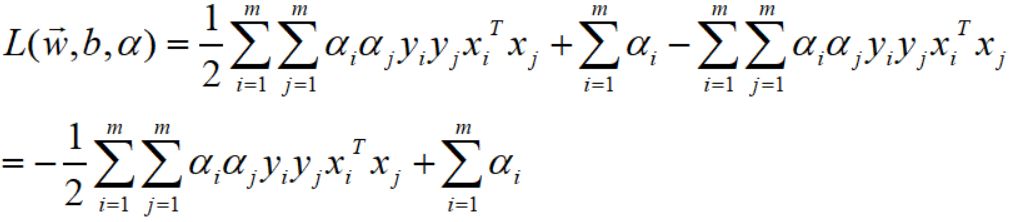
目标函数终于变为系数的函数,接下来使用KKT求解上式的最优解。关于 KKT 的理解,可以先尝试理解拉格朗日乘子法,而它的推导可借助下面这些图更加容易理解
仅含等式约束 仅含不等式约束 等式和不等式约束混合型
拉格朗日乘数法、KKT条件为什么就能求出极值。1 仅含等式约束
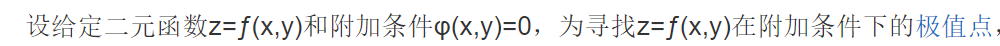
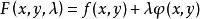

2 找找 sense
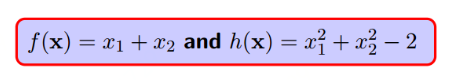
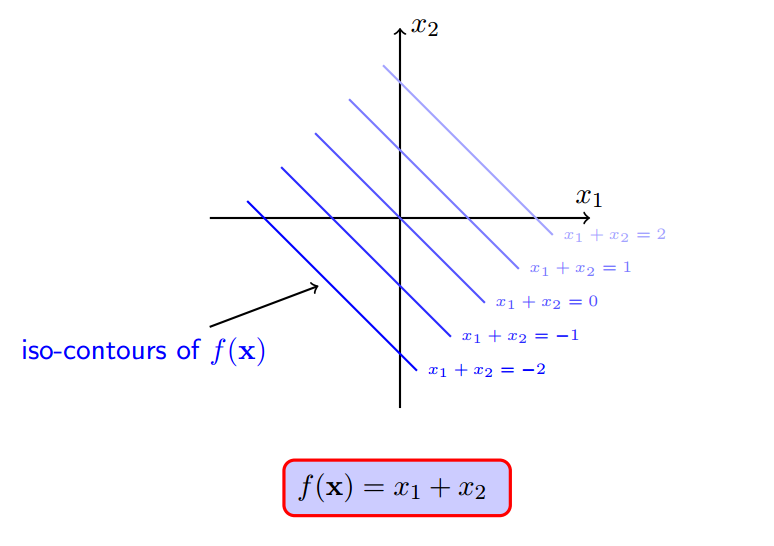
h(x)注定会约束f(x)不会等于100,不会等于10000...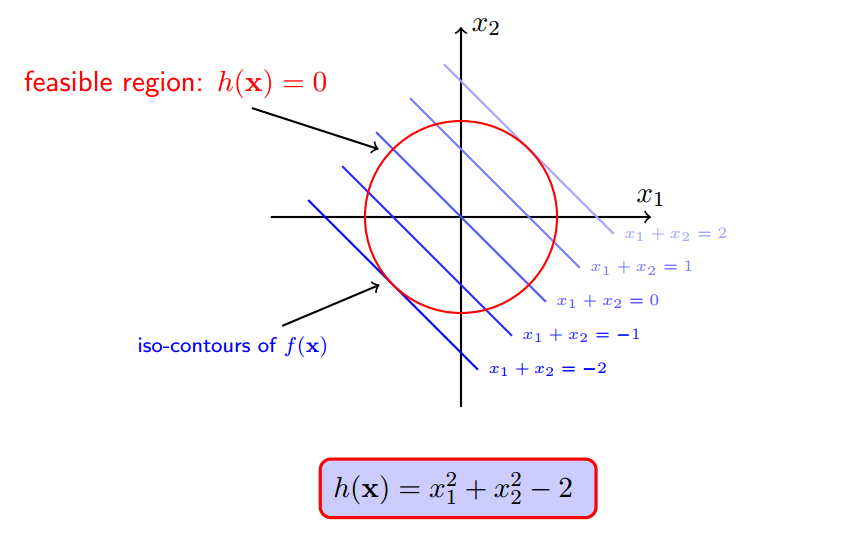
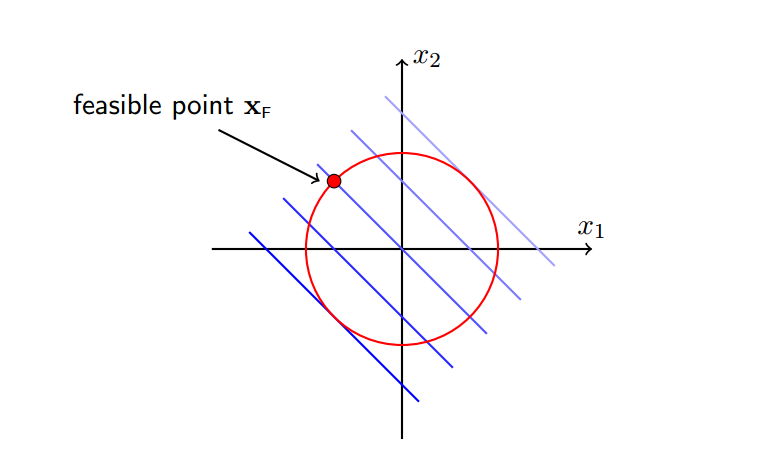
3 梯度下降
我们想要寻找一个移动x的规则,使得移动后f(x+delta_x)变小,当然必须满足约束h(x+delta_x)=0
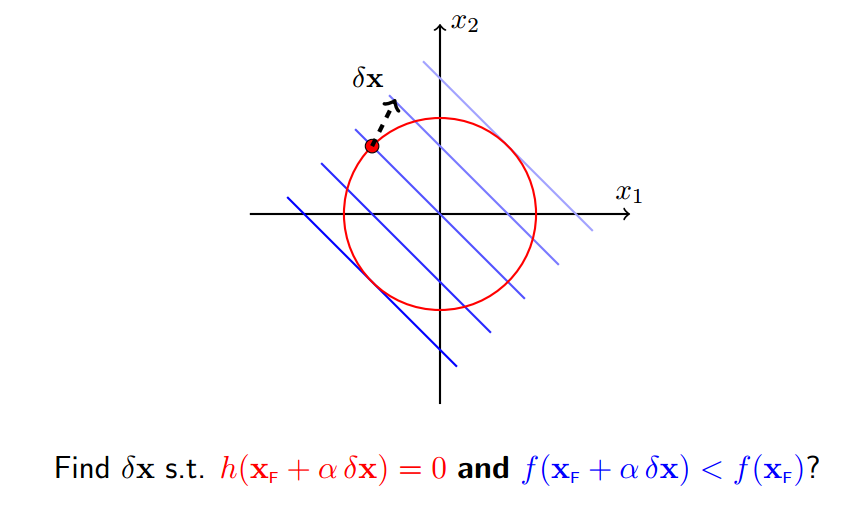 使得
使得f(x)减小最快的方向就是它的梯度反方向,即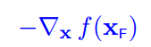
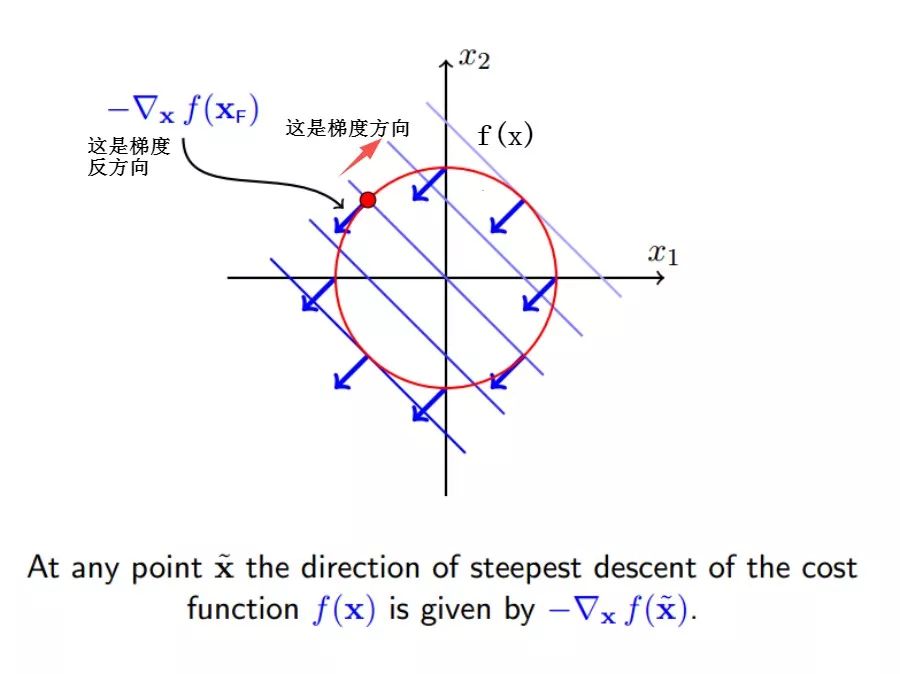
f(x+delta_x)就会变小,转化为公式就是: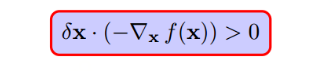
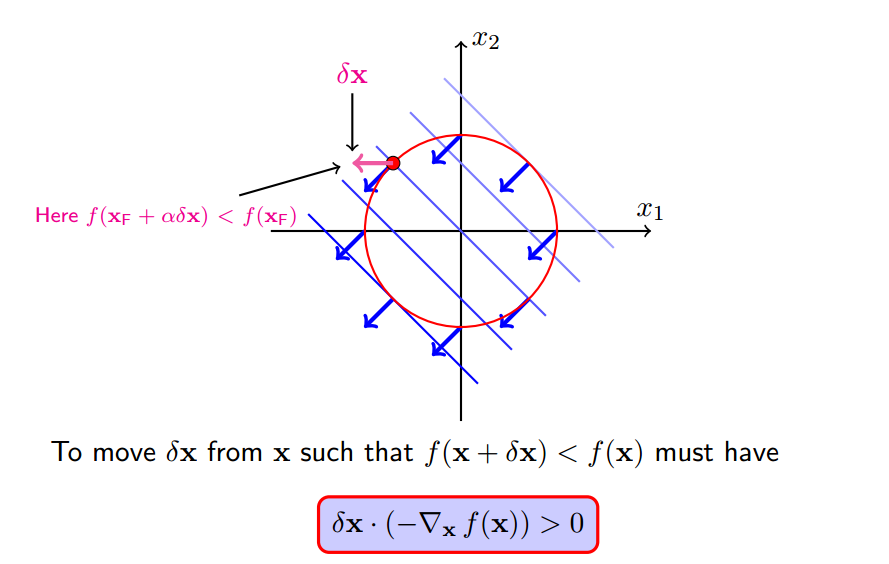
4 约束面的法向
约束面的外法向:
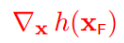
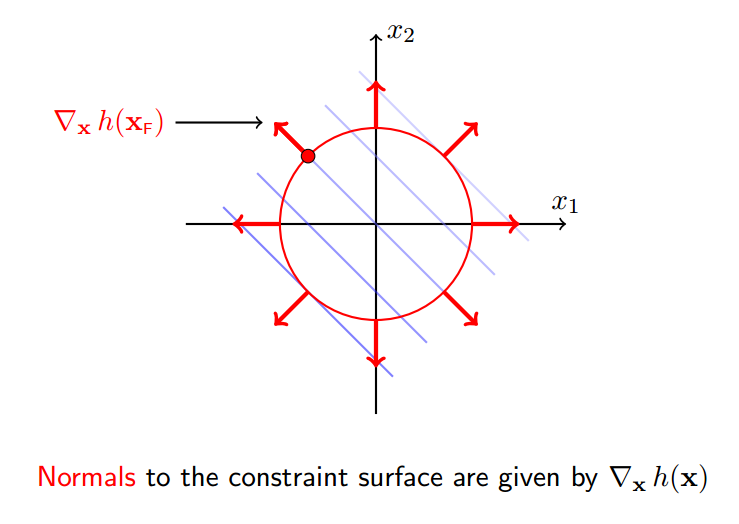
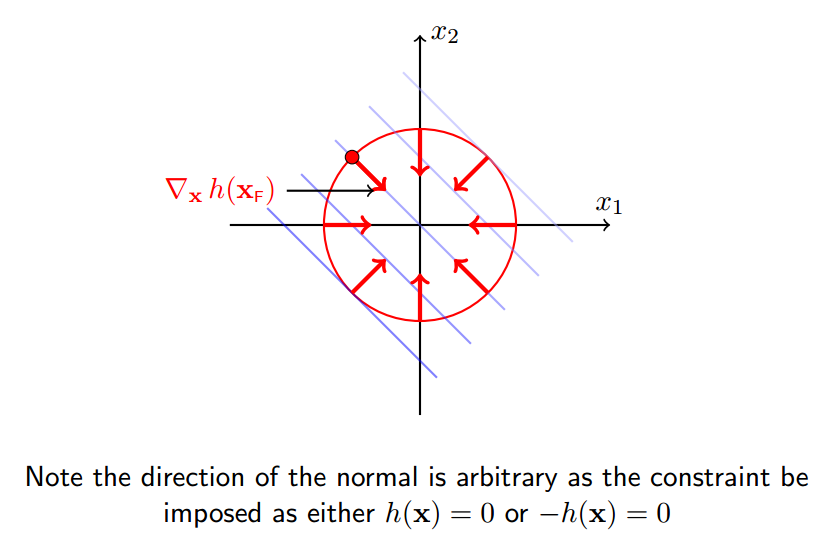
绿圈表示法向的正交方向
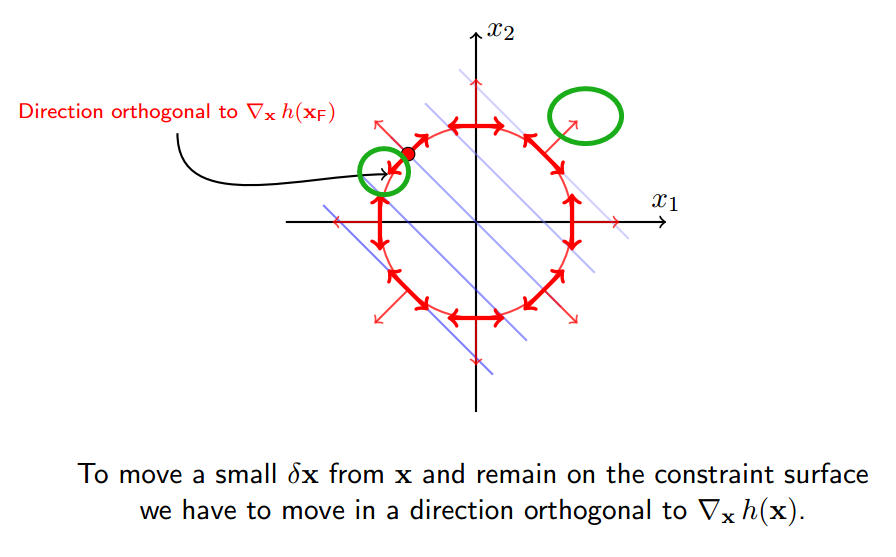
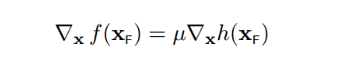
根据第四小节讲述,delta_x必须正交于h(x),所以:
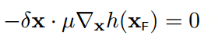
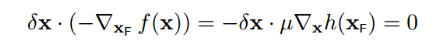
至此,我们就找到f(x)偏导数等于0的点,就是下图所示的两个关键点(它们也是f(x)与h(x)的临界点)。且必须满足以下条件,也就是两个向量必须是平行的:
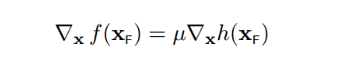
6 完全解码拉格朗日乘数法
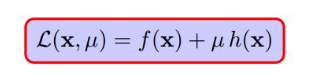
还有取得极值的的三个条件,都是对以上五个小节中涉及到的条件的编码

关于第三个条件,稍加说明。
对于含有多个变量,比如本例子就含有2个变量x1, x2,就是一个多元优化问题,需要求二阶导,二阶导的矩阵就被称为海塞矩阵(Hessian Matrix)
与求解一元问题一样,仅凭一阶导数等于是无法判断极值的,需要求二阶导,并且二阶导大于0才是极小值,小于0是极大值,等于0依然无法判断是否在此点去的极值。
交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

