各种梯度下降优化算法回顾和总结
↓推荐关注↓
不管是使用PyTorch还是TensorFlow,用多了Optimizer优化器封装好的函数,对其内部使用的优化算法却没有仔细研究过,也很难对其优点和缺点进行实用的解释。所以打算以这一篇论文为主线并结合多篇优秀博文,回顾和总结目前主流的优化算法,对于没有深入了解过的算法,正好借这个机会学习一下。
写在前面
计算目标函数关于当前参数的梯度: 根据历史梯度计算一阶动量和二阶动量: , 计算当前时刻的下降梯度: 根据下降梯度进行更新:
鞍点:一个光滑函数的鞍点邻域的曲线,曲面,或超曲面,都位于这点的切线的不同边。例如这个二维图形,像个马鞍:在x-轴方向往上曲,在y-轴方向往下曲,鞍点就是(0,0)。

指数加权平均、偏差修正:可参见这篇文章
Gradient Descent(GD)
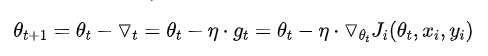
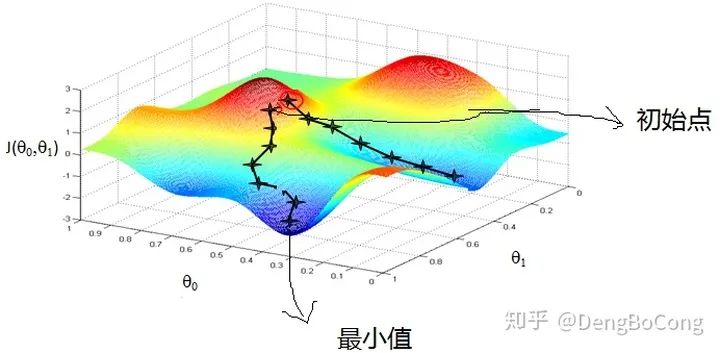
训练速度慢:在应用于大型数据集中,每输入一个样本都要更新一次参数,且每次迭代都要遍历所有的样本,会使得训练过程及其缓慢,需要花费很长时间才能得到收敛解。 容易陷入局部最优解:由于是在有限视距内寻找下山的反向,当陷入平坦的洼地,会误以为到达了山地的最低点,从而不会继续往下走。所谓的局部最优解就是鞍点,落入鞍点,梯度为0,使得模型参数不在继续更新。
Batch Gradient Descent(BGD)
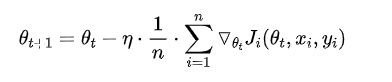
Stochastic Gradient Descent(SGD)
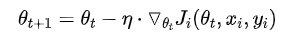
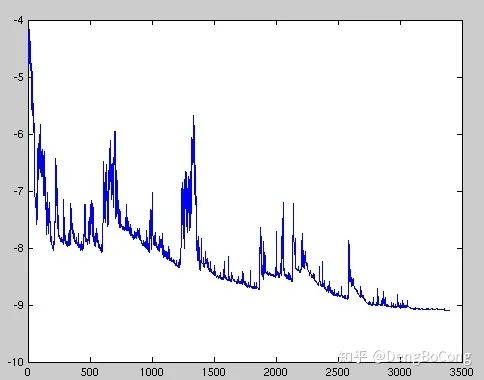
虽然看起来SGD波动非常大,会走很多弯路,但是对梯度的要求很低(计算梯度快),而且对于引入噪声,大量的理论和实践工作证明,只要噪声不是特别大,SGD都能很好地收敛。 应用大型数据集时,训练速度很快。比如每次从百万数据样本中,取几百个数据点,算一个SGD梯度,更新一下模型参数。相比于标准梯度下降法的遍历全部样本,每输入一个样本更新一次参数,要快得多。
SGD在随机选择梯度的同时会引入噪声,使得权值更新的方向不一定正确(次要)。 SGD也没能单独克服局部最优解的问题(主要)。
Mini-batch Gradient Descent(MBGD,也叫作SGD)
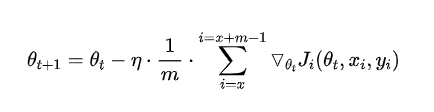
Mini-batch gradient descent 不能保证很好的收敛性,learning rate 如果选择的太小,收敛速度会很慢,如果太大,loss function 就会在极小值处不停地震荡甚至偏离(有一种措施是先设定大一点的学习率,当两次迭代之间的变化低于某个阈值后,就减小 learning rate,不过这个阈值的设定需要提前写好,这样的话就不能够适应数据集的特点)。
对于非凸函数,还要避免陷于局部极小值处,或者鞍点处,因为鞍点所有维度的梯度都接近于0,SGD 很容易被困在这里(会在鞍点或者局部最小点震荡跳动,因为在此点处,如果是BGD的训练集全集带入,则优化会停止不动,如果是mini-batch或者SGD,每次找到的梯度都是不同的,就会发生震荡,来回跳动)。SGD对所有参数更新时应用同样的 learning rate,如果我们的数据是稀疏的,我们更希望对出现频率低的特征进行大一点的更新, 且learning rate会随着更新的次数逐渐变小。
Momentum
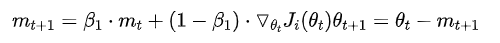
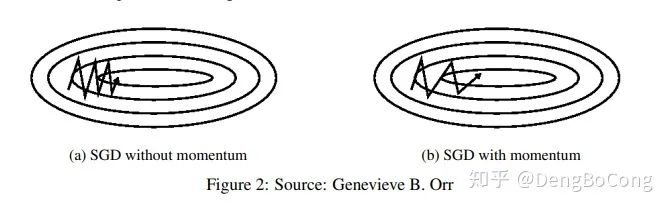
随机梯度的方法(引入的噪声) Hessian矩阵病态问题(可以理解为SGD在收敛过程中和正确梯度相比来回摆动比较大的问题)。
Nesterov Accelerated Gradient
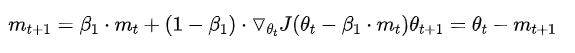
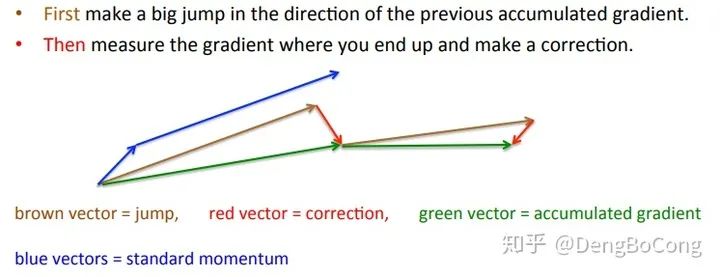
加上nesterov项后,梯度在大的跳跃后,进行计算对当前梯度进行校正。下图是momentum和nesterrov的对比表述图如下:
Adagrad
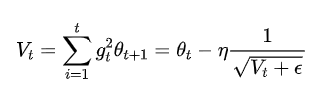
仍需要手工设置一个全局学习率 , 如果 设置过大的话,会使regularizer过于敏感,对梯度的调节太大 中后期,分母上梯度累加的平方和会越来越大,使得参数更新量趋近于0,使得训练提前结束,无法学习
Adadelta
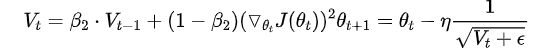
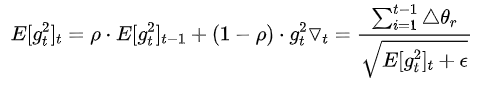
训练初中期,加速效果不错,很快 训练后期,反复在局部最小值附近抖动
RMSprop
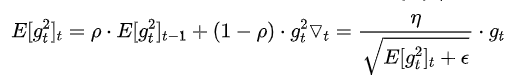
其实RMSprop依然依赖于全局学习率 RMSprop算是Adagrad的一种发展,和Adadelta的变体,效果趋于二者之间 适合处理非平稳目标(包括季节性和周期性)——对于RNN效果很好
Adaptive Moment Estimation(Adam)
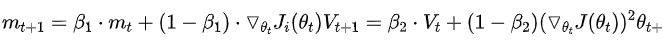
Adam梯度经过偏置校正后,每一次迭代学习率都有一个固定范围,使得参数比较平稳。 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点 为不同的参数计算不同的自适应学习率 也适用于大多非凸优化问题——适用于大数据集和高维空间。
AdaMax
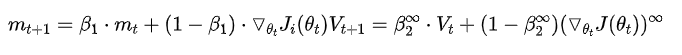
Nadam
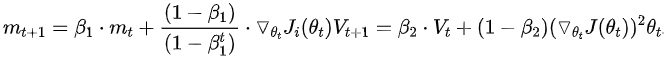
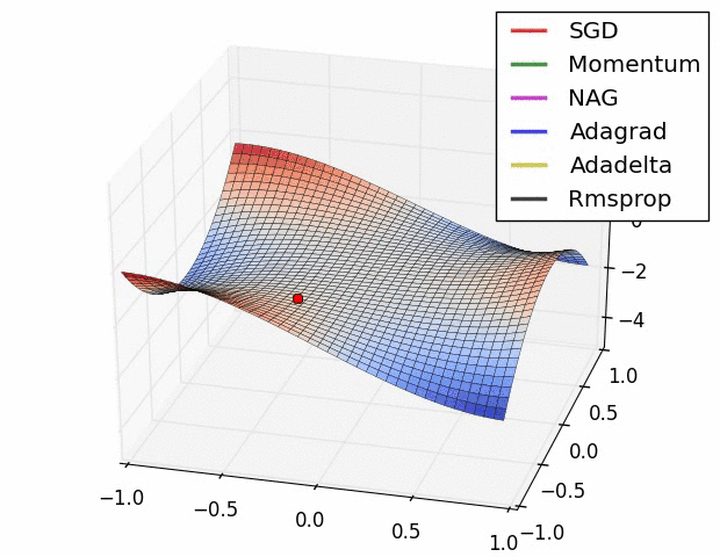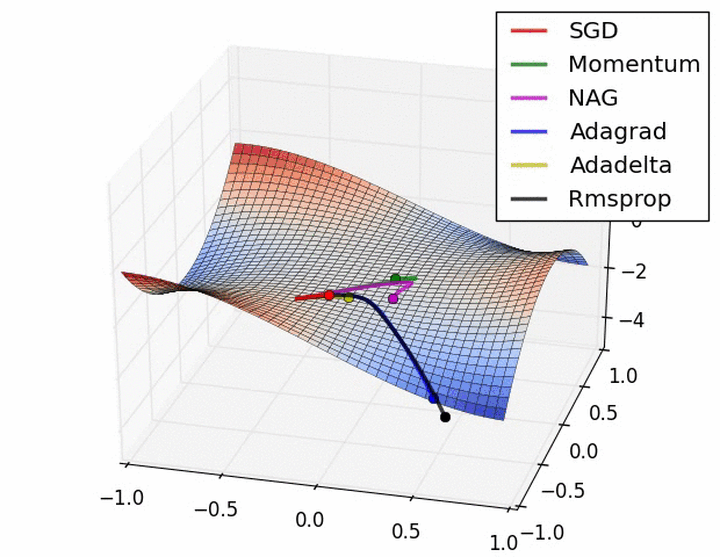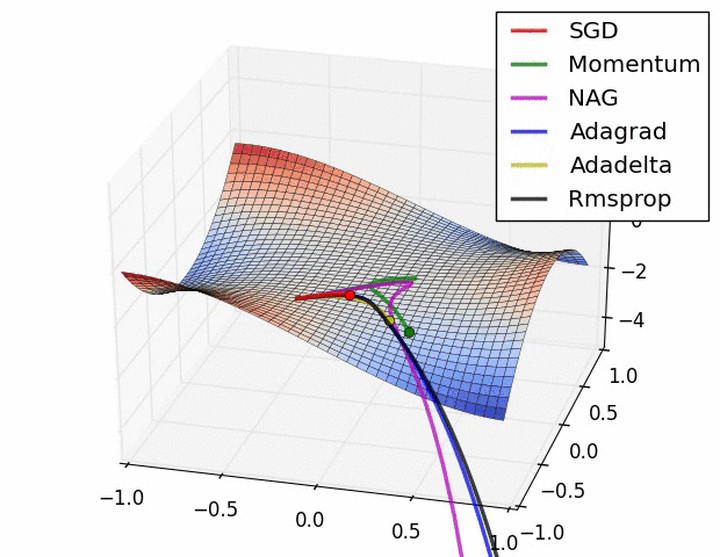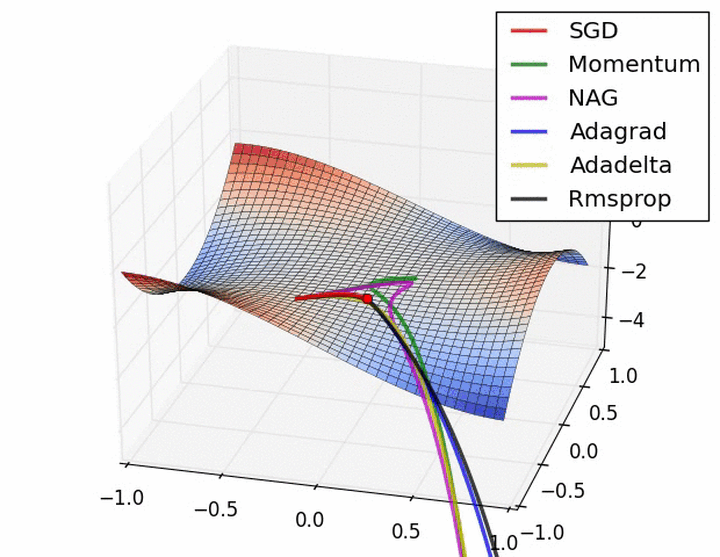
下图描述了在一个曲面上,6种优化器的表现:
下图在一个存在鞍点的曲面,比较6中优化器的性能表现:
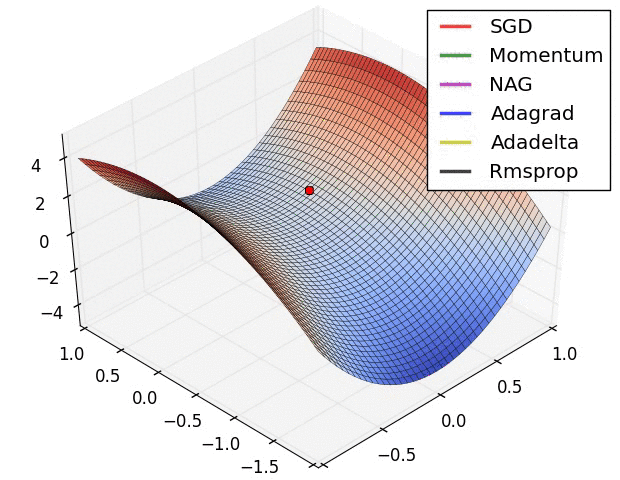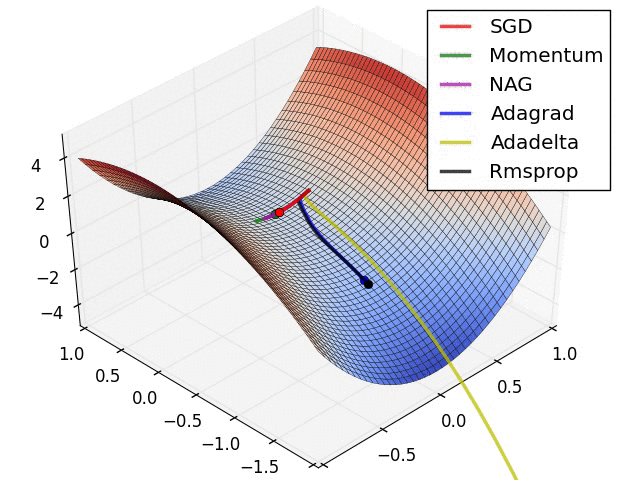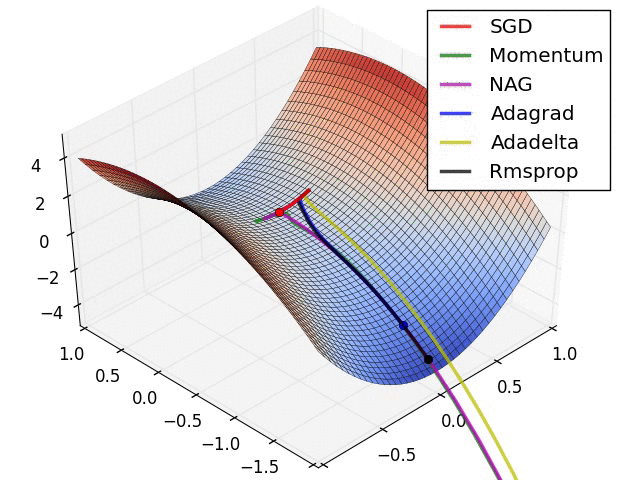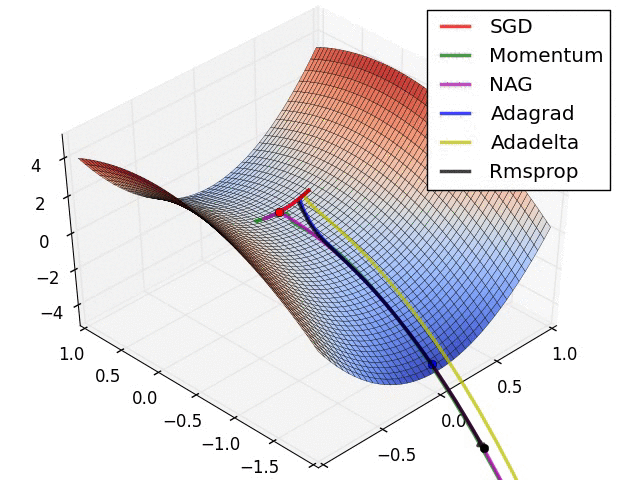
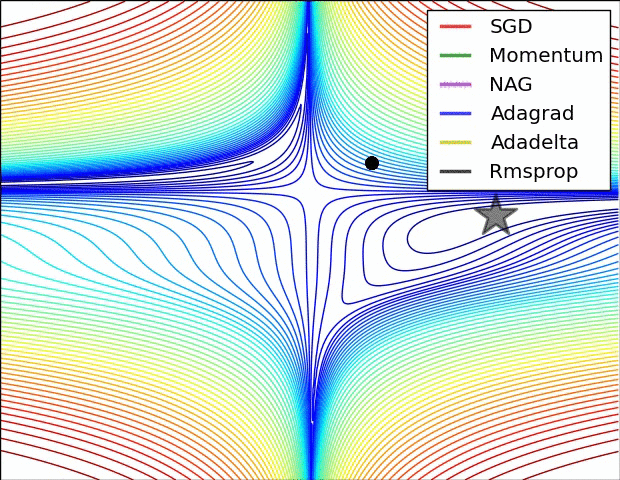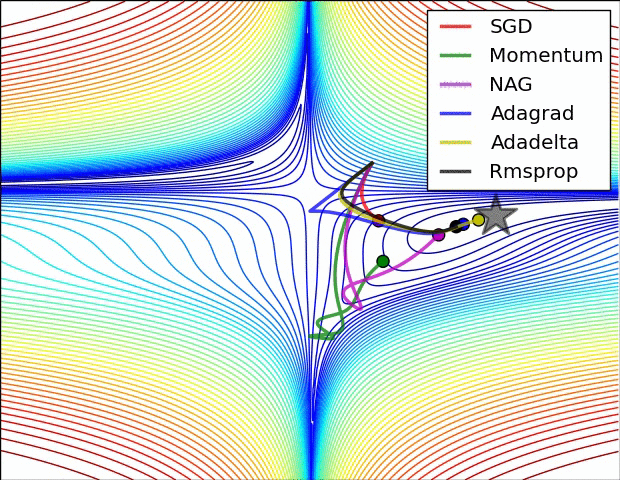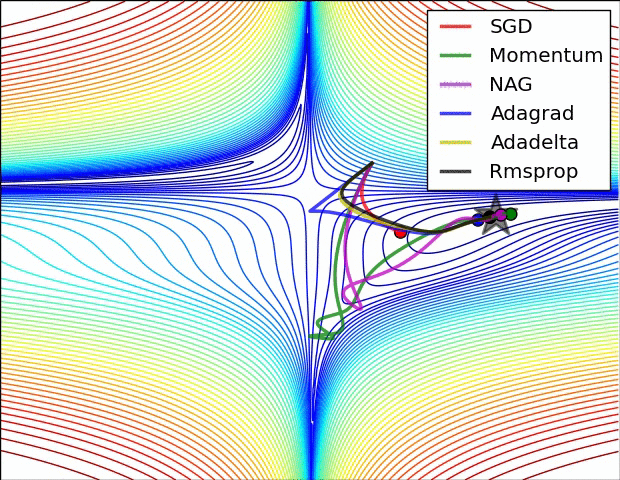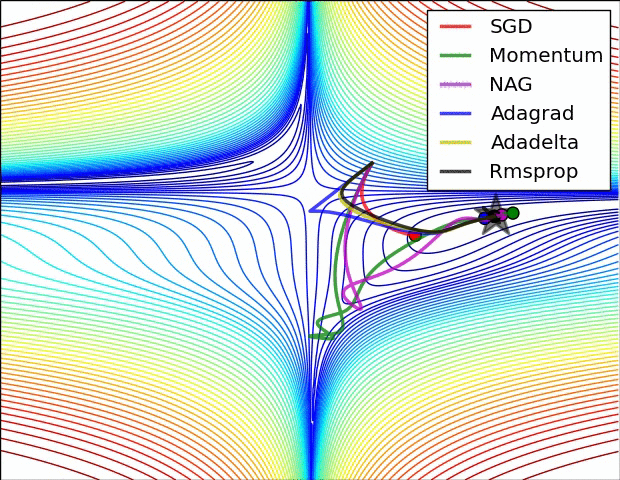
下图图比较了6种优化器收敛到目标点(五角星)的运行过程
总结
对于稀疏数据,尽量使用学习率可自适应的优化方法,不用手动调节,而且最好采用默认值 SGD通常训练时间更长,但是在好的初始化和学习率调度方案的情况下,结果更可靠 如果在意更快的收敛,并且需要训练较深较复杂的网络时,推荐使用学习率自适应的优化方法。 Adadelta,RMSprop,Adam是比较相近的算法,在相似的情况下表现差不多。 在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果 如果验证损失较长时间没有得到改善,可以停止训练。 添加梯度噪声(高斯分布 )到参数更新,可使网络对不良初始化更加健壮,并有助于训练特别深而复杂的网络。
An overview of gradient descent optimization algorithms(https://ruder.io/optimizing-gradient-descent/) 深度学习最全优化方法总结比较(SGD,Adagrad,Adadelta,Adam,Adamax,Nadam)(https://zhuanlan.zhihu.com/p/22252270) visualize_optimizers(https://github.com/snnclsr/visualize_optimizers) lossfunctions(https://lossfunctions.tumblr.com/) 优化算法Optimizer比较和总结(https://zhuanlan.zhihu.com/p/55150256) 一个框架看懂优化算法之异同 SGD/AdaGrad/Adam(https://zhuanlan.zhihu.com/p/32230623) 深度学习——优化器算法Optimizer详解(BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam)(https://www.cnblogs.com/guoyaohua/p/8542554.html) 机器学习:各种优化器Optimizer的总结与比较(https://blog.csdn.net/weixin_40170902/article/details/80092628) optimizer优化算法总结(https://blog.csdn.net/muyu709287760/article/details/62531509#%E4%B8%89%E7%A7%8Dgradient-descent%E5%AF%B9%E6%AF%94)
论文标题:An overview of gradient descent optimization algorithms
原文链接:https://arxiv.org/pdf/1609.04747.pdf
Github:NLP相关Paper笔记和代码复现(https://github.com/DengBoCong/nlp-paper)
说明:阅读论文时进行相关思想、结构、优缺点,内容进行提炼和记录,论文和相关引用会标明出处,引用之处如有侵权,烦请告知删除。
长按或扫描下方二维码,后台回复:加群,即可申请入群。一定要备注:来源+研究方向+学校/公司,否则不拉入群中,见谅!
(长按三秒,进入后台)
推荐阅读
评论

