学习编译原理Time10 ~ NFA转化为DFA及算法实现
开门见山,直接举个例子:
下图为NFA:
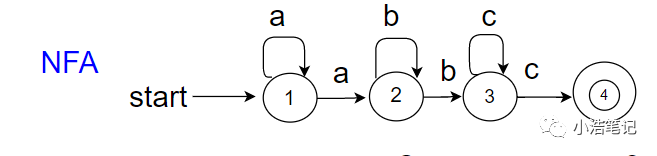
当状态1的时候遇到字符a的时候,可以进入状态2,也可以进入状态1;而状态2的时候遇到状态字符的时候,可以进入状态3,也可以进入状态2,以此类推......
接下来谈等价转换:
1、DFA的初始状态还是NFA的的初始状态
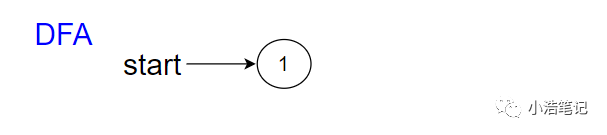
2、当遇到字符a的时候,既可以进入状态2,也可以进入状态1,且不确定进入状态2还是进入状态1,但还是可以确定二者中的一个,因此构造了一个新的状态,由状态1和状态2组成的集合

3、当这个新的状态遇到字符a的是仍然进入这个新的状态
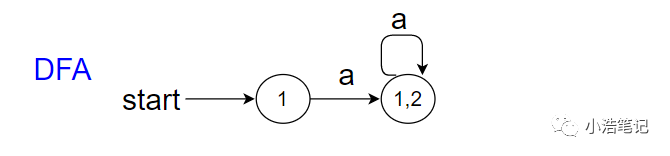
4、以此类推,最终转化为DFA
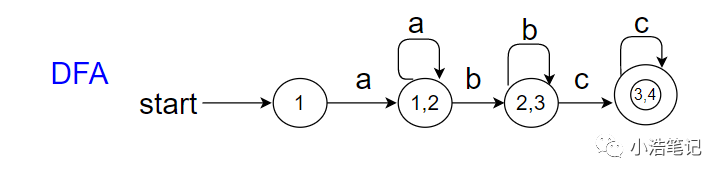
子集构造法:
输入:NFA
输出:接收同样语言的DFA
方法:一开始,ε-closure(s0)是Dstates中唯一状态,且它为加标记;
while(在Dstates中有一个未标记状态T)
{
给T加上标记;
for(每个输入符号a)
{
U=ε-closure(move(T,a));
if(U不在Dstates中)
将U加入到Dstates中,且不加记;
Dtran[T,a]=U;
}
}| 操作 | 描述 |
| ε-closure(s) | 能够从NFA的状态s开始只通过ε转换到达的NFA状态集合 |
| ε-closure(T) | 能够从T中的某个NFA状态s开始只通过ε转换到达的NFA状态集合 |
| move(T,a) | 能够从T中的某个状态s出发通过标号为a的转换到达的NFA状态的集合 |
计算ε-closure(T)
将T的所有状态压入stack中;
将ε-closure(T)初始化为T;
while(stack非空)
{
将栈顶元素t给弹出栈中;
for(每个满足如下条件的u:从t出发有一个标号为ε的转换到达状态)
if(u不在ε-closure(T)中)
{
将u加入到ε-closure(T)中;
将u压入栈中;
}
}
小浩笔记

评论
