常见排序算法原理及JS代码实现
来源:SegmentFault 思否社区
作者:Warren

本文只是将作者学习的过程以及算法理解进行简单的分享,提供多一个角度的理解说明,或许让你的困惑能得以解决(代码或说明若有问题,欢迎留言、联系更正!以免造成更多困惑)
如果要更深入研究这些算法的同学,社区中同类型更优秀,单个算法更深入剖析的文章也是比比皆是,这里或许作为一个常见排序算法入门学习了解更准确
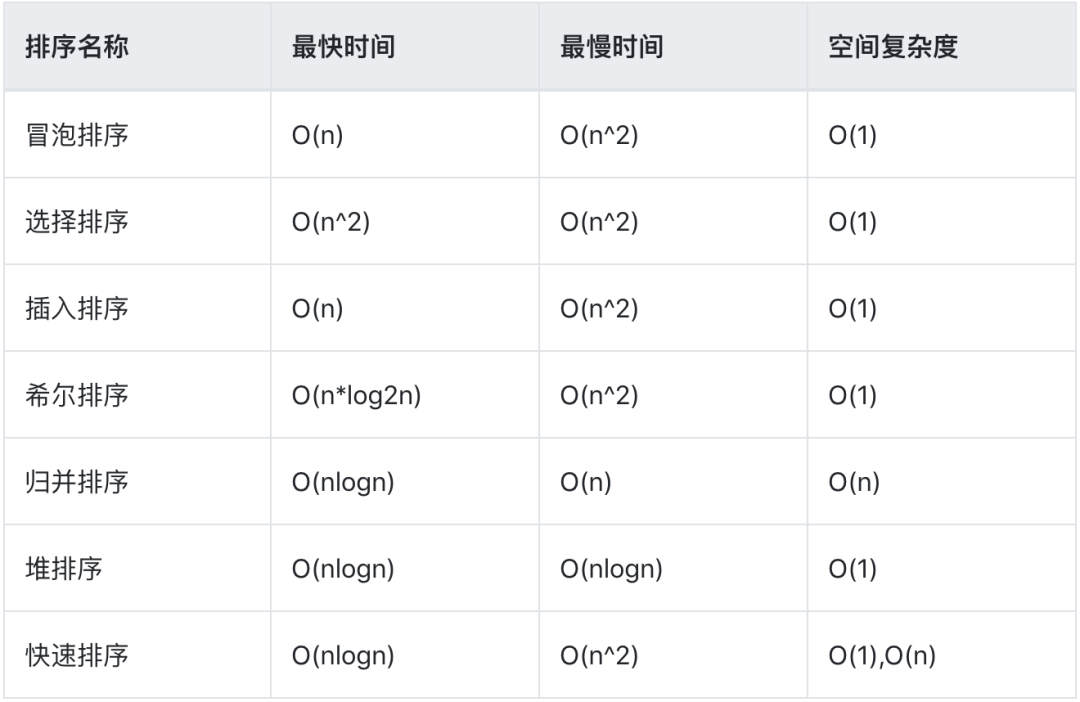
以上时间和空间复杂度会根据算法的优化有所不同
生成测试所用,包含随机十万条数据的数组
const arr = []for (let i = 0; i < 100000; i++) {arr.push(Math.random())}
以下标注的时间均为对该随机数组的数据排序的时间,这里的时间只是作为一个参考,因为并没有控制到只有唯一变量(每个排序算法用到的数组长度相同,但数组值不同),所以这里的时间只反应常规情况
运行时间的计算使用 console.time()
数组 sort() 方法
实现也是基于快排做了很多的优化算法,以保障各种情况都能稳定较快的实现排序 查看C++实现源码
时间:≈ 75ms
function sortCompare(array) {array.sort((a, b) => (a-b))}
冒泡排序
原理:依次比较两个相邻的元素,将较大的放到右边(升序排列)
一轮循环只找到一个最值,然后通过多次这样的循环(所以有两层嵌套循环),获得一个排序结果
以下是经过简单优化的算法实现:
时间:≈ 21899ms
function bubbling(array) {const len = array.lengthlet sorted = true/* 每找到一个最值,需要一次循环 */for (let i = 0; i < len; i++) {/* 必须每轮循环前,假设是排好序后的数组,防止只需要前几次循环就排好的情况 */sorted = true/* 这里的循环是找出当前轮的最值 *//* len-1-i 保障 j+1 能取到,同时放到最后的数,不用参与下一轮的循环,因为它已经是上一轮找出的最值 */for (let j = 0; j < len - 1 - i; j++) {if (array[j] > array[j + 1]) {let temp = array[j]array[j] = array[j + 1]array[j + 1] = tempsorted = false}}/* 如果是已经排好序了就直接退出循环,此时最优时间复杂度 O(n) */if (sorted) break}return array}
选择排序
原理:从剩余未排序序列中找到最小(大)元素,放置在已排序序列的末尾位置,以此循环,直到所有元素均排序完毕
时间:≈ 6353ms
function selectionSort(array) {let len = array.lengthfor (let i = 0; i < len; i++) {/* 默认开始的第一个值的位置放置下一个最小值 */let minIndex = i/* 查找剩余数值中的最小值,从 i + 1 开始的目的是避免与自身进行一次比较 */for (let j = i + 1; j < len; j++) {if(array[minIndex] > array[j]) {minIndex = j}}/* 将最小值和当前位置(i)的值进行交换 */let temp = array[minIndex]array[minIndex] = array[i]array[i] = temp}return array}
插入排序
原理:将未排序队列中的数值,逐个与已排序队列中的数进行比较,当出现大于或小于已排序队列中的某个数时,进行插入操作
注意与选择排序的区别,选择排序是在未排序的数中找最值,然后交换位置,插入排序则是在已排序的的数中找对应的第一个相对最值
时间:≈ 2416ms
function insertionSort(array) {let len = array.lengthfor (let i = 1; i < len; i++) {/* 记录当前未排序的数,该数将会和有序数列中的数进行比较 */let current = array[i]/* 有序数列的最后一个数(如果是从小到大排列,也就是最大的数) */let endIndex = i - 1while (endIndex >=0 && array[endIndex] > current) {/* 将有序数列中的数,逐一与当前未排序数进行比较直到,找出比当前未排序数小的数即停止 */array[endIndex + 1] = array[endIndex]endIndex--}/* 将最后一个往后移动空出来的位置赋值为,当前未排序数 */array[endIndex+1] = current}return array}
希尔排序
原理:
插入排序的一种优化
设置一个增量,将数组中的数按此增量进行分组(比如增量为4,那下标为0,4,8...的数为一组) 对分组的数进行插入排序 缩小增量 重复步骤1、2、3,直到增量为1 当增量为1时,对整个数组进行一次插入排序,输出最后结果
时间复杂度与增量选取有关,以下算法时间复杂度为 O(n^(3/2))
非稳定排序(2个相等的数,在排序完成后,原来在前面的数还是在前面,即为稳定排序)
时间:≈ 35ms
function shellSort(array) {let len = array.length, gap = 1;/* 此处获取一个最大增量,增量的获取方法不固定,这里采用比较常见的方式,一定要保证最后能取到1 */while(gap < len/3) {gap = gap*3+1;}/* 每更新一次增量就进行一次插入排序 */while(gap>0) {/* 以下逻辑与插入排序一致,当增量变为1时即完全一致 */for (let i = gap; i < len; i++) {/* 这里要循环到数组最后是因为要保障当前分组中的每一个数都经过排序,所以当前分组靠前的数据会被与后面的数据进行多次排序 */let current = array[i]let endIndex = i - gapwhile(endIndex>=0 && array[endIndex] > current) {array[endIndex + gap] = array[endIndex]endIndex -= gap}array[endIndex+gap] = current}gap = Math.floor(gap/3)}return array}
分治法:把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并
归并排序
原理:将当前数组,递归分组,比较大小后再一 一合并分组,是采用分治法的一个应用
获取一个中间位置的值,然后以该位置为中心点分组 递归进行分组 比较当前两个分组,将其合并为一个数组
时间:≈ 1170ms
function mergeSort(array) {const len = array.lengthif(len<2) return arrayconst middle = Math.floor(len/2)/* 取中间值进行分组 */const left = array.slice(0, middle)const right = array.slice(middle)/* 递归分组 */return merge(mergeSort(left), mergeSort(right))}function merge(left, right) {const result = []/* 两个分组都有值时,逐个进行比较 */while (left.length && right.length) {if(left[0] <= right[0]) {result.push(left.shift())} else {result.push(right.shift())}}/* 只有一个分组时,表明其全部为最大值,直接全部放入结果数组即可 */if(left.length){result.push(...left)}if(right.length){result.push(...right)}return result}
堆排序
分为大顶堆(子节点都小于父节点),小顶堆(子节点都大于父节点)
原理:
根据给定的数据创建堆 将堆顶和堆尾互换,将堆长度减1 递归步骤1、2
时间:≈ 46ms
function heapSort(array) {let length = array.length/* 第一个非叶子节点(叶子节点:没有子节点的节点):n/2 -1 *//* 为什么从这个点开始,也是因为这是最后一个拥有子节点的父节点,其可能会发生父子节点交换 */const node = Math.floor(length/2) - 1/* 第一步先将数组构建为堆 这里是大顶堆 */for (let i = node; i >= 0 ; i--) {maxHeap(array, i, length)}/* 第二步 将堆顶元素与堆尾元素交换 再将前 (n-1) 个数重复构建堆 */for (let j = length - 1; j > 0; j--) {swap(array, 0, j)length--/* 这里相当于把第一个叶子节点改变了,所以下面从 0 开始, 当前堆的堆尾前一个数为结束 重新构建堆 */maxHeap(array, 0, length)}return array}function maxHeap(array, i, length) {/* 左子节点 */let left = i*2 + 1/* 右子节点 */let right = i*2 + 2/* 父节点 */let parent = i/* 找出子节点中比父节点大的数进行交换 */if(left < length && array[left] > array[parent]) {parent = left}/* 这里两个条件都触发也没有关系,只要保障,一个比父节点大的子节点被移上去即可 */if(right < length && array[right] > array[parent]) {parent = right}if(parent !== i) {swap(array,i, parent)/* 表示有数据移动,所以要重排一下数据移动后,所影响到的父子节点,也就是此时的 parent 节点和其子节点 */maxHeap(array, parent, length)}}function swap(arr, i, j) {var temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
快速排序
原理:
在数组中找一个基准 数组中的数与该基准相比较,比它小的放在其前面,比它大的放在其后面(分区操作) 再递归的去操作基准前、后的分区
方式一:
需要 O(n) 的额外存储空间,和归并排序一样
但是代码更清晰的体现快排的思想
时间:≈ 77ms
function quickSort (array) {if (array.length < 2) return array;const pivot = array[0];let left = []let right = []for (let i = 1, length = array.length; i < length; i++) {if(array[i] < pivot) {left.push(array[i])} else {right.push(array[i])}}return quickSort(left).concat([pivot], quickSort(right));}
方式二:
原地排序
时间:≈ 34ms
function quickSort(array, left, right) {if(left<right) {pivotIndex = fill(array, left, right)quickSort(array, left, pivotIndex-1)quickSort(array, pivotIndex+1, right)}return array}function fill(array, left, right) {const pivotValue = array[left]while(left < right){/* 右边大于基准的数据不需要移动位置 *//* 这里或下面的循环,一定要确保有一处把相等的情况包含在内 */while(array[right] >= pivotValue && left < right){right--}/* 将右边第一个扫描到的小于基准的数据移动到左边的空位 */array[left] = array[right]/* 左边小于基准的数据不需要移动位置 */while(array[left] < pivotValue && left < right){left++}array[right] = array[left]}/* 这里right和left 相等了 */array[right] = pivotValuereturn right}
还有一些更好的优化,比如基准数的选取,避免最坏时间复杂度情况的发生,可自行探索
总结:
在实际项目中可能直接用到这些算法就能解决掉业务需求的情况并不多,甚至直接用 Array.sort() 也能解决。
但是业务需求千变万化,多种多样,总有需要你从底层去更改、优化、变异算法的情况,此时就需要用你理解的这些基本算法的原理来快速解决业务问题。

