点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

无论是什么优化算法，最后都可以用一个简单的公式抽象：

是参数，而是参数的增量，而各种优化算法的主要区别在于对的计算不同，本文总结了下面十个优化算法的公式，以及简单的Python实现：

SGD
Momentum
Nesterov Momentum
AdaGrad
RMSProp
AdaDelta
Adam
AdaMax
Nadam
NadaMax

SGD

虽然有凑数的嫌疑，不过还是把SGD也顺带说一下，就算做一个符号说明了。常规的随机梯度下降公式如下：

其中是学习率，是损失关于参数的梯度（有的资料中会写成等形式），不过相比SGD，用的更多的还是小批量梯度下降（mBGD）算法，不同之处在于一次训练使用多个样本，然后取所有参与训练样本梯度的平均来更新参数，公式如下：

其中是第次训练中个样本损失关于参数梯度的均值，如无特别声明，下文所出现也遵循该定义

另外或者在下面的优化算法中，只是作为一个传入的变量，其具体的计算是由其他模块负责，可以参考下面两个链接：

Numpy实现神经网络框架(3)——线性层反向传播推导及实现

https://zhuanlan.zhihu.com/p/67854272

卷积核梯度计算的推导及实现

https://zhuanlan.zhihu.com/p/64248652

Momentum

Momentum，也就是动量的意思。该算法将梯度下降的过程视为一个物理系统，下图是在百度图片中找的（侵删）

如上图所示，在该物理系统中有一个小球（质点），它所处的水平方向的位置对应为

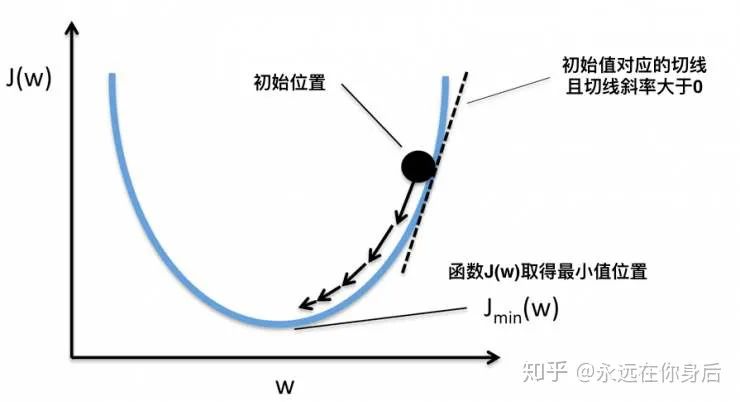
的值，而垂直方向对应为损失。设其质量

，在第

时刻，在单位时间内，该质点受外力而造成的动量改变为：

(1.1)到(1.2)是因为

，所以约去了。另外受到的外力可以分为两个分量：重力沿斜面向下的力

和粘性阻尼力

令

代入(1.2)式中：

然后对“位置”进行更新：

所以这里

，另外

的方向与损失的梯度方向相反，并取系数为

，得到：

代入(1.4)，得到速度的更新公式：

进一步的，将(1.6)式展开，可以得到：

可以看出来是一个变相的等比数列之和，且公比小于1，所以存在极限，当

足够大时，

趋近于

实现代码

import numpy as np

class Momentum(object):
    def __init__(self, alpha=0.9, lr=1e-3):
        self.alpha = alpha  # 动量系数
        self.lr = lr        # 学习率
        self.v = 0          # 初始速度为0

    def update(self, g: np.ndarray):    # g = J'(w) 为本轮训练参数的梯度
        self.v = self.alpha * self.v - self.lr * g  # 公式
        return self.v    # 返回的是参数的增量，下同

以上是基于指数衰减的实现方式，另外有的Momentum算法中会使用指数加权平均来实现，主要公式如下：

不过该方式因为

，刚开始时

会比期望值要小，需要进行修正，下面的Adam等算法会使用该方式

Nesterov Momentum

Nesterov Momentum是Momentum的改进版本，与Momentum唯一区别就是，Nesterov先用当前的速度

更新一遍参数，得到一个临时参数

，然后使用这个临时参数计算本轮训练的梯度。相当于是小球预判了自己下一时刻的位置，并提前使用该位置的梯度更新：

为了更加直观，还是上几个图吧，以下是Momentum算法

的更新过程：

假设下一个位置的梯度如下：

那么Nesterov Momentum就提前使用这个梯度进行更新：

整体来看Nesterov的表现要好于Momentum，至于代码实现的话因为主要变化的是

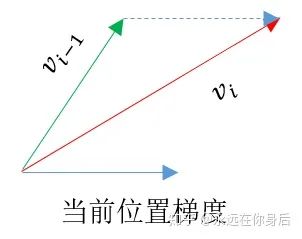
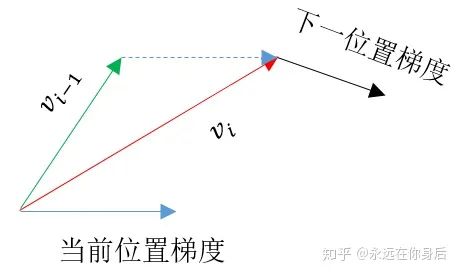
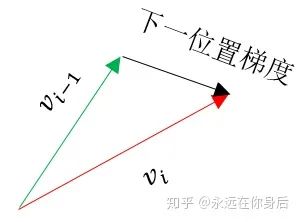
，所以可以之前使用Momentum的代码

AdaGrad

AdaGrad全称为Adaptive Subgradient，其主要特点在于不断累加每次训练中梯度的平方，公式如下：

其中

是一个极小的正数，用来防止除0，而

，

是矩阵的哈达玛积运算符，另外，本文中矩阵的平方或者两矩阵相乘都是计算哈达玛积，而不是计算矩阵乘法

从公式中可以看出，随着算法不断迭代，

会越来越大，整体的学习率会越来越小。所以，一般来说AdaGrad算法一开始是激励收敛，到了后面就慢慢变成惩罚收敛，速度越来越慢

对于代码实现，首先将

展开得到：

通常

，所以在第一次训练时(2.2)式为：

因为每次训练

的值是不确定的，所以要防止处0，但是可以令

，这样就可以在(2.2)式中去掉

将

代入(2.3)式，可以得到：

可知

恒大于0，因此不必在计算

中额外加入

，代码如下：

class AdaGrad(object):
    def __init__(self, eps=1e-8, lr=1e-3):
        self.r = eps    # r_0 = epsilon
        self.lr = lr

    def update(self, g: np.ndarray):
        r = r + np.square(g)
        return -self.lr * g / np.sqrt(r)

RMSProp

RMSProp是AdaGrad的改进算法，其公式和AdaGrad的区别只有

的计算不同，先看公式

可以看出，与AdaGrad不同，RMSProp只会累积近期的梯度信息，对于“遥远的历史”会以指数衰减的形式放弃

并且AdaGrad算法虽然在凸函数(Convex Functions)上表现较好，但是当目标函数非凸时，算法梯度下降的轨迹所经历的结构会复杂的多，早期梯度对当前训练没有太多意义，此时RMSProp往往表现更好

以下是将

展开后的公式：

与AdaGrad一样，令

，从而去掉计算

时的

，实现代码：

class RMSProp(object):
    def __init__(self, lr=1e-3, beta=0.999, eps=1e-8):
        self.r = eps
        self.lr = lr
        self.beta = beta

    def update(self, g: np.ndarray):
        r = r * self.beta + (1-self.beta) * np.square(g)
        return -self.lr * g / np.sqrt(r)

AdaDelta

AdaDelta是与RMSProp相同时间对立发展出来的一个算法，在实现上可以看作是RMSProp的一个变种，先看公式：

可以看到该算法不需要设置学习率

，这是该算法的一大优势。除了同样以

来累积梯度的信息之外，该算法还多了一个

以指数衰减的形式来累积

的信息

与前面相同，令：

然后去掉(3.1)中的

，得到：

这样的话可以减少一些计算，代码如下：

class AdaDelta(object):
    def __init__(self, beta=0.999, eps=1e-8):
        self.r = eps
        self.s = eps
        self.beta = beta

    def update(self, g: np.ndarray):
        g_square = (1-self.beta) * np.square(g)     # (1-beta)*g^2
        r = r * self.beta + g_square
        frac = s / r
        res = -np.sqrt(frac) * g
        s = s * self.beta + frac * g_squaretmp      # 少一次乘法。。。
        return res

关于以上几个算法的对比：

其中NAG是Nesterov Momentum

更多关于AdaDelta的信息，可以参考这篇文章：自适应学习率调整：AdaDelta（https://www.cnblogs.com/neopenx/p/4768388.html）

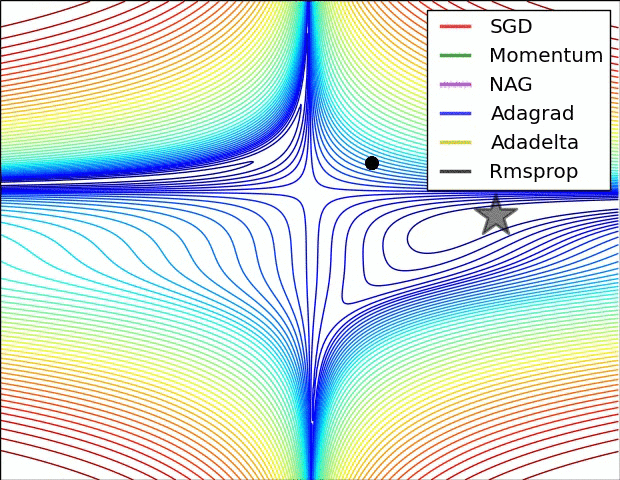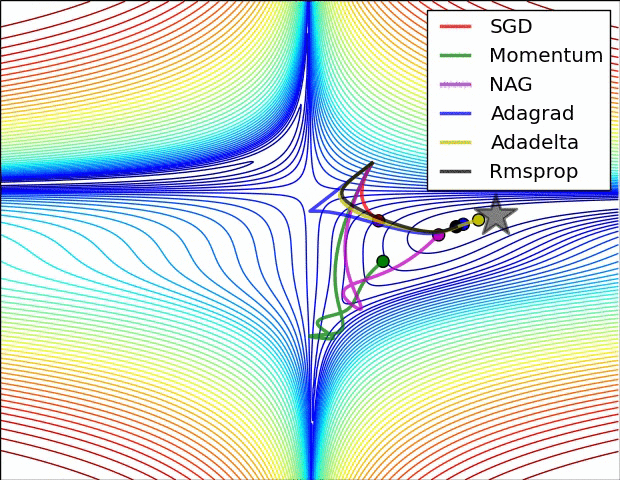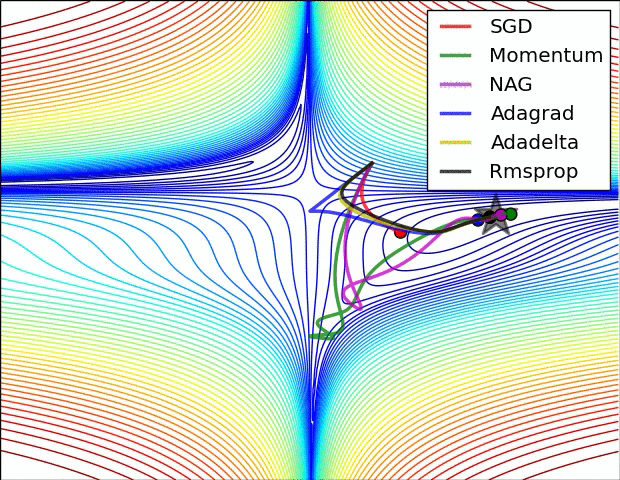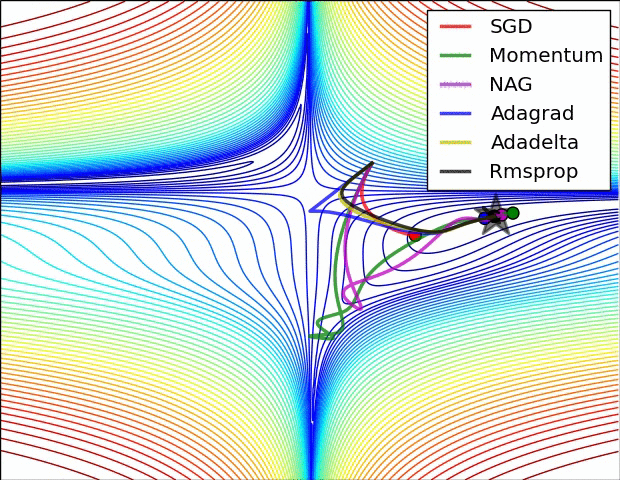
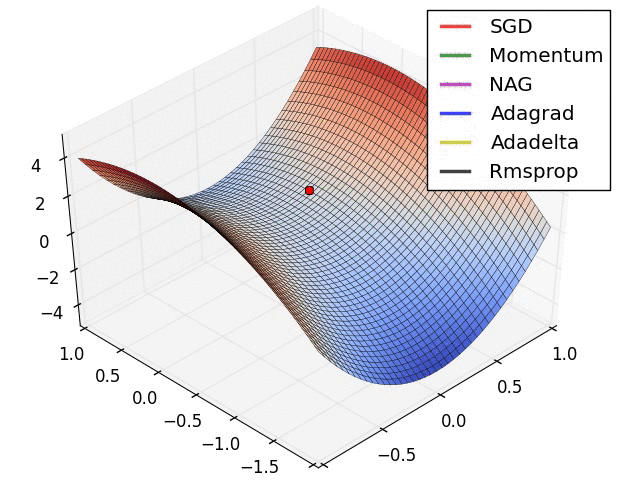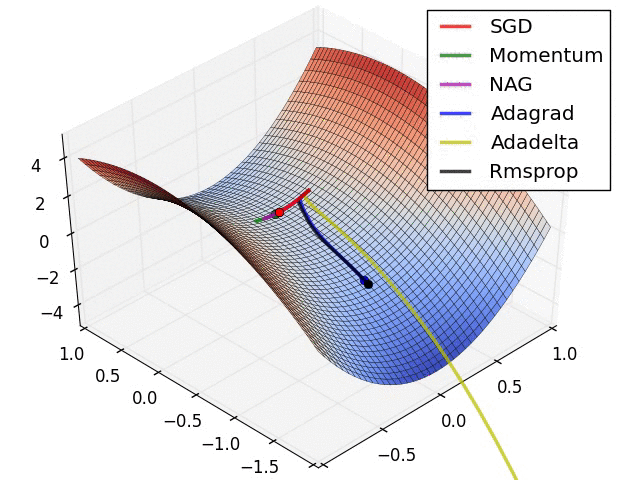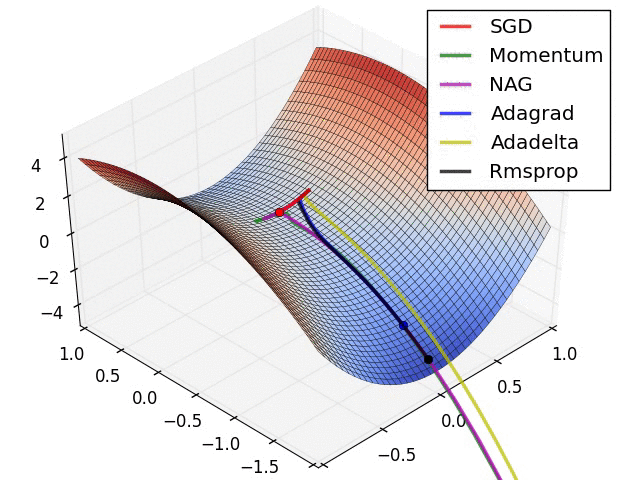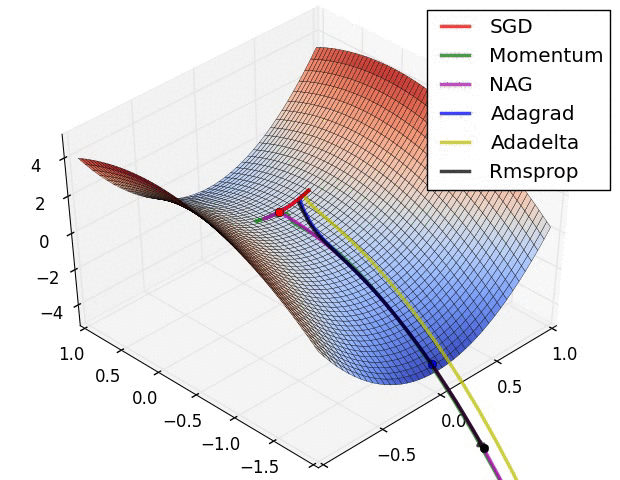
Adam

Adam的名称来自Adaptive Momentum，可以看作是Momentum与RMSProp的一个结合体，该算法通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率，公式如下：

(4.1)和(4.2)在Momentum和RMSProp中已经介绍过了，而不直接使用

计算

却先经过(4.3)和(4.4)式是因为通常会设

，所以此时梯度的一阶矩估计和二阶矩估是有偏的，需要进行修正

虽然没办法避免修正计算，但是还是可以省去一些计算过程，初始化时令：

然后(4.5)式变为：

因为

，可知当

足够大时修正将不起作用（也不需要修正了）：

代码如下：

class Adam(object):
    def __init__(self, lr=1e-3, alpha=0.9, beta=0.999, eps=1e-8):
        self.s = 0
        self.r = eps
        self.lr = lr
        self.alpha = alpha
        self.beta = beta
        self.alpha_i = 1
        self.beta_i = 1

    def update(self, g: np.ndarray):
        self.s = self.s * self.alpha + (1-self.alpha) * g
        self.r = self.r * self.beta + (1-self.beta) * np.square(g)
        self.alpha_i *= self.alpha
        self.beta_i *= self.beta_i
        lr = -self.lr * (1-self.beta_i)**0.5 / (1-self.alpha_i)
        return lr * self.s / np.sqrt(self.r)

AdaMax

首先回顾RSMSProp中

的展开式并且令

，得到：

可以看到这相当于是一个

的

范数，也就是说

的各维度的增量是根据该维度上梯度的

范数的累积量进行缩放的。如果用

范数替代就得到了Adam的不同变种，不过其中

范数对应的变种算法简单且稳定

对于

范数，第

轮训练时梯度的累积为：

然后求无穷范数：

由此再来递推

：

需要注意，这个max比较的是梯度各个维度上的当前值和历史最大值，具体可以结合代码来看，最后其公式总结如下：

另外，因为

是累积的梯度各个分量的绝对值最大值，所以直接用做分母且不需要修正，代码如下：

class AdaMax(object):
    def __init__(self, lr=1e-3, alpha=0.9, beta=0.999):
        self.s = 0
        self.r = 0
        self.lr = lr
        self.alpha = alpha
        self.alpha_i = 1
        self.beta = beta

    def update(self, g: np.ndarray):
        self.s = self.s * self.alpha + (1-self.alpha) * g
        self.r = np.maximum(self.r*self.beta, np.abs(g))
        self.alpha_i *= self.alpha
        lr = -self.lr / (1-self.alpha_i)
        return lr * self.s / self.r

Nadam

Adam可以看作是Momentum与RMSProp的结合，既然Nesterov的表现较Momentum更优，那么自然也就可以把Nesterov Momentum与RMSProp组合到一起了，首先来看Nesterov的主要公式：

为了令其更加接近Momentum，将(5.1)和(5.2)修改为：

然后列出Adam中Momentum的部分：

将(5.5)和(5.6)式代入到(5.7)式中：

将上式中标红部分进行近似：

代入原式，得到：

接着，按照(5.4)式的套路，将

替换成

，得到：

整理一下公式：

同样令

，消去(5.8)式种的

：

代码

class Nadam(object):
    def __init__(self, lr=1e-3, alpha=0.9, beta=0.999, eps=1e-8):
        self.s = 0
        self.r = eps
        self.lr = lr
        self.alpha = alpha
        self.beta = beta
        self.alpha_i = 1
        self.beta_i = 1

    def update(self, g: np.ndarray):
        self.s = self.s * self.alpha + (1-self.alpha) * g
        self.r = self.r * self.beta + (1-self.beta) * np.square(g)
        self.alpha_i *= self.alpha
        self.beta_i *= self.beta_i
        lr = -self.lr * (1-self.beta_i)**0.5 / (1-self.alpha_i)
        return lr * (self.s * self.alpha + (1-self.alpha) * g) / np.sqrt(self.r)

NadaMax

按照同样的思路，可以将Nesterov与AdaMax结合变成NadaMax，回顾以下(5.8)式：

然后是AdaMax的二阶矩估计部分：

用(6.2)式替换掉(6.1)式中标红部分，得到：

最后，整理公式：

代码实现：

class NadaMax(object):
    def __init__(self, lr=1e-3, alpha=0.9, beta=0.999):
        self.s = 0
        self.r = 0
        self.lr = lr
        self.alpha = alpha
        self.alpha_i = 1
        self.beta = beta

    def update(self, g: np.ndarray):
        self.s = self.s * self.alpha + (1-self.alpha) * g
        self.r = np.maximum(self.r*self.beta, np.abs(g))
        self.alpha_i *= self.alpha
        lr = -self.lr / (1-self.alpha_i)
        return lr * (self.s * self.alpha + (1-self.alpha) * g) / self.r

好消息！
小白学视觉知识星球
开始面向外开放啦👇👇👇



下载1：OpenCV-Contrib扩展模块中文版教程
在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~

收藏 | 从SGD到NadaMax，深度学习十种优化算法原理及实现

SGD

Numpy实现神经网络框架(3)——线性层反向传播推导及实现

卷积核梯度计算的推导及实现

Momentum

Nesterov Momentum

AdaGrad

RMSProp

AdaDelta

Adam

AdaMax

Nadam

NadaMax