【机器学习基础】四个小项目完全解读支持向量机
支持向量机算法的基础是最大间隔分类器,最大间隔分类器虽然很简单,但不能应用于大部分数据,因为大部分属是非线性数据,无法用线性分类器进行分类,解决方案是对特征空间进行核函数映射,然后再运行最大间隔分类器。
本文跳过枯燥乏味的算法推导过程,循序渐进的介绍支持向量机分类原理,并通过四个小项目快速的理解支持向量机的线性分类,非线性分类和参数调参过程。
最大间隔分类器使用超平面进行分类。
什么是超平面?
假如特征空间是 p 维,超平面就是 p-1维,为了可视化超平面,假设特征空间是3个维度的,那么超平面是2维的。
超平面表达式如下:
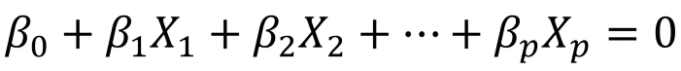
如果数据的特征满足上式,那么该点落在超平面上,若不满足,则该点处于超平面的两侧。
超平面如下图:
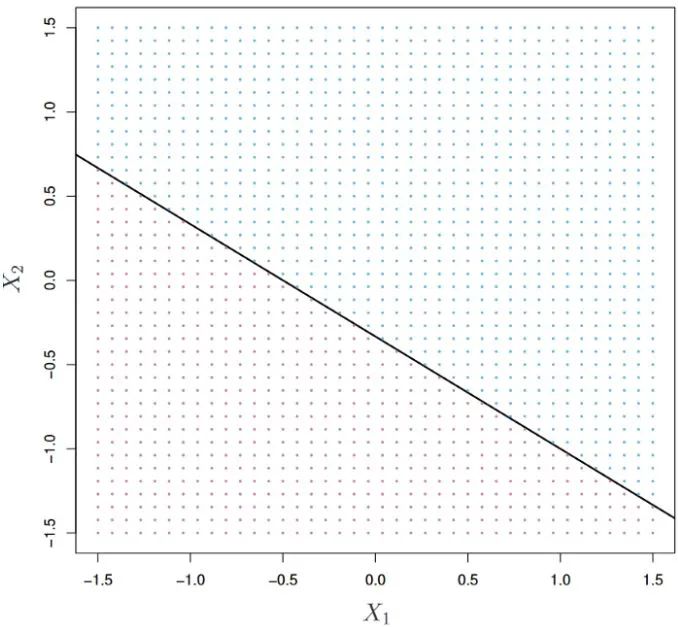
一般来说,如果数据可以用超平面完美地进行分离,那么超平面的数量是无限的,因为它可以向上移动、向下移动,或者对该超平面进行小角度的选择而不与观测数据接触。
超平面是无限的,如何选择最优超平面?
最优超平面是离观测点最远的分离超平面,在给定超平面的情况下,我们计算每个训练数据到超平面的距离,这就是所谓的间隔,最优超平面也就是间隔最大的分类器。如下图:
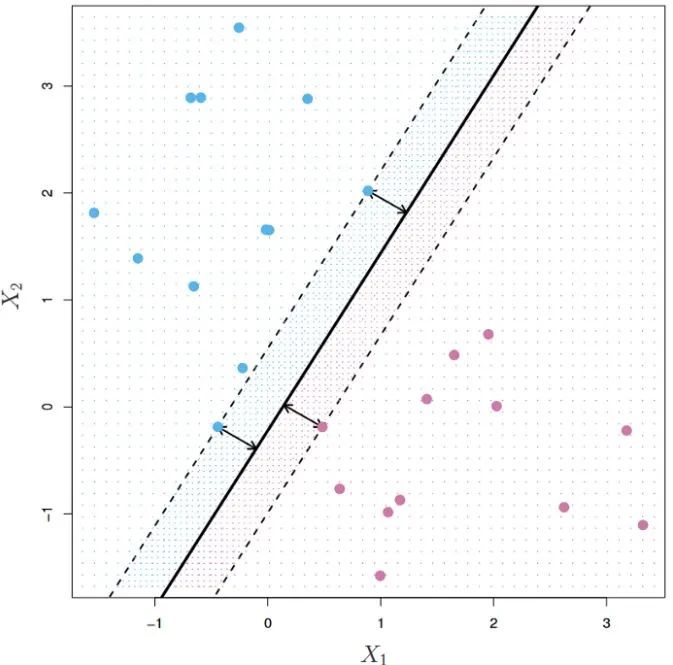
正如你所看到的,有三个观测点到超平面的距离相等,这三个观测点就是支持向量,若这三个观测点的位置改变了,超平面也会相应的改变。最大间隔分类器的性能只与这三个点相关,与其他数据不相关,看到这里,是不是对支持向量机算法有了新的收获了?
如果数据分布是非线性的,不能用超平面进行分类,如下图:
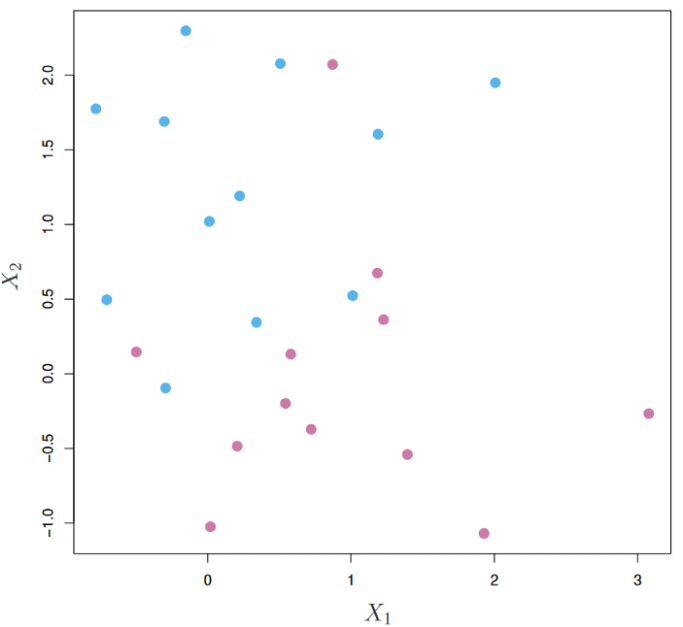
对于这样的数据分布,我们将使用核函数映射为新的特征空间,再运行最大间隔分类器进行分类,这种方法称为支持向量机。
支持向量机的核函数映射是一种扩展特征空间的方法,核函数的核心思想是计算两个数据点的相似度。核函数的度没有限制,使用度大于1的内核可以得到更灵活的决策边界,如下图所示:
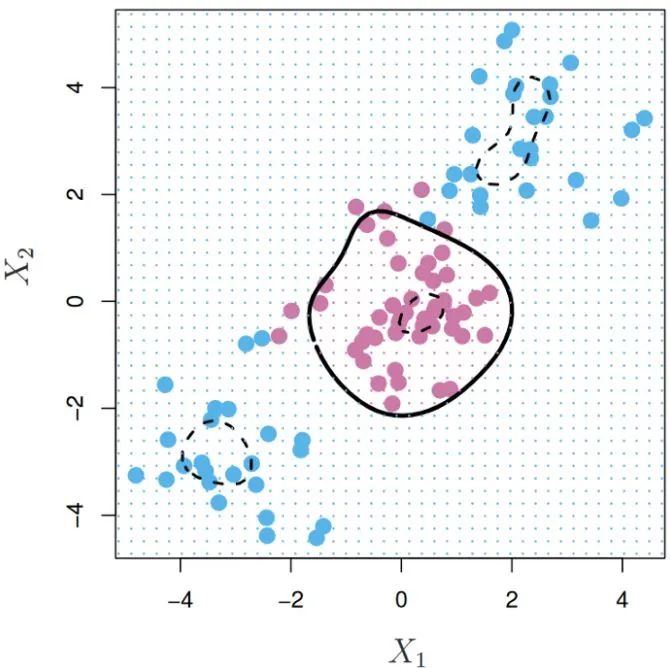
为了更好的理解核函数的选择是如何影响SVM算法,我们在四个不同的场景实现它。
项目1——线性核支持向量机
在开始之前,让我们导入一些有用的库:

导入需要训练和测试的数据路径:

定义可多次调用的画图函数:

散点图可视化数据:

散点图如下:
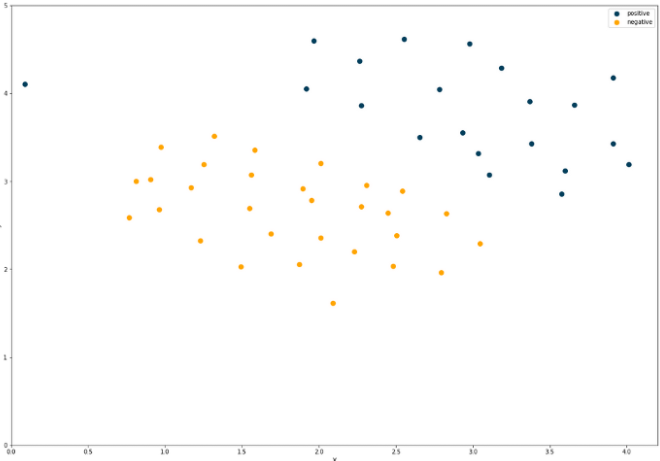
线性核支持向量机对该数据进行分类,其中正则化参数C=1,并使用预测值绘制超平面(hyperplane),如下图:
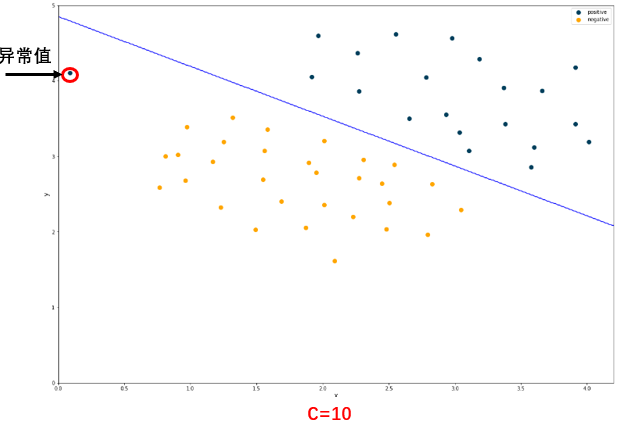
由上图的分类结果可知,当正则化参数等于1时,模型对异常值不敏感。因此,低的正则化参数往往泛化能力更好,测试误差率大于验证误差率。
若增加正则化参数C等于100,那么模型对异常点异常敏感,分类结果如下图:
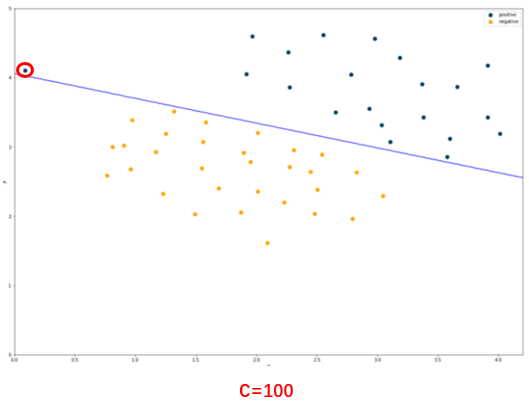
由上图结果可知:C=100时,异常值能够正确分类,但是分类超平面与样本点的距离非常近,可以推断该模型处于过拟合状态,泛化能力差。
项目2——高斯核支持向量机
若分类边界是非线性的,我们常常使用高斯核进行SVM分类。
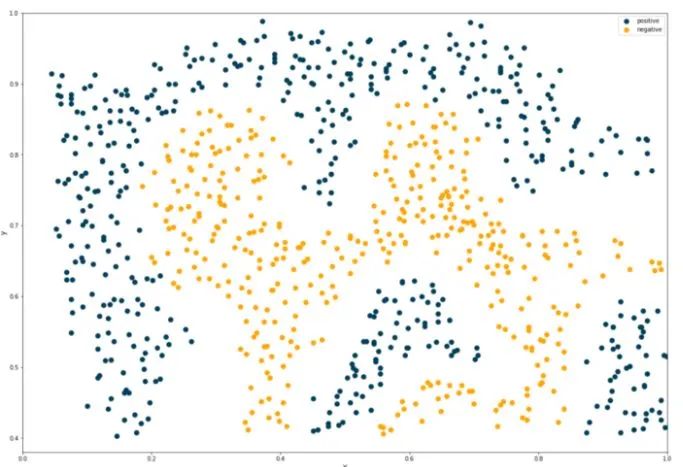
首先,可视化需要分类的数据:

散点图:
高斯核用来衡量两个数据点的相似度,公式如下:
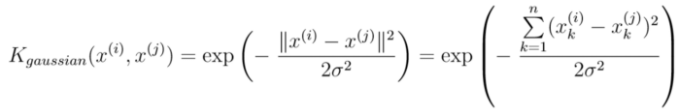
其中参数σ决定相似度指标趋于零的速度。
高斯核支持向量机训练和预测代码:

预测结果及分类边界如下图:
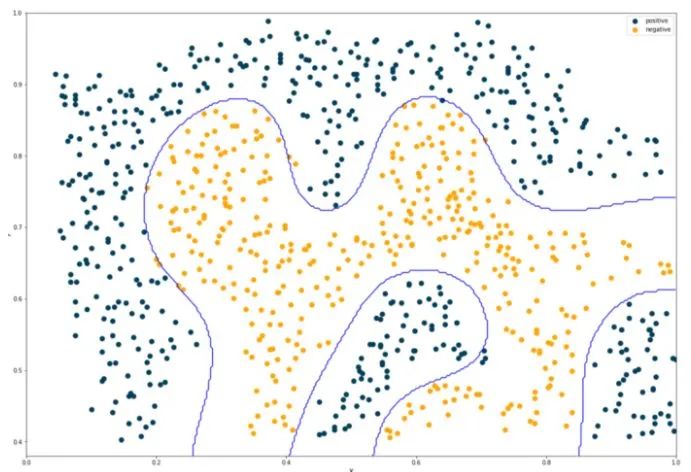
项目3——支持向量机调参
本节介绍用交叉验证方法选择模型最优参数,首先下载数据集:

图形如下:
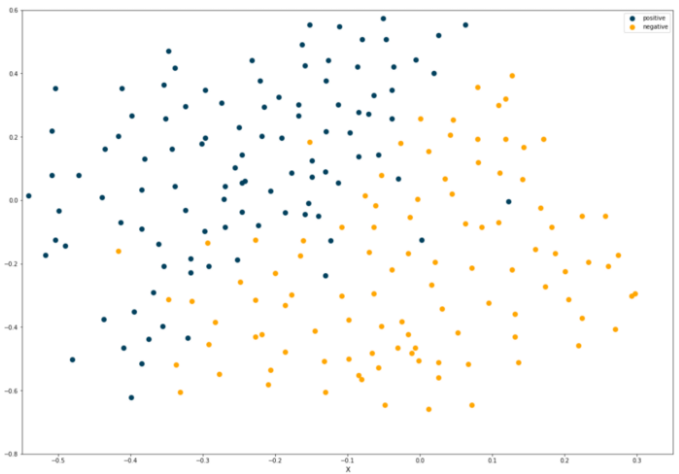
使用交叉验证方法选择最优参数,代码如下:

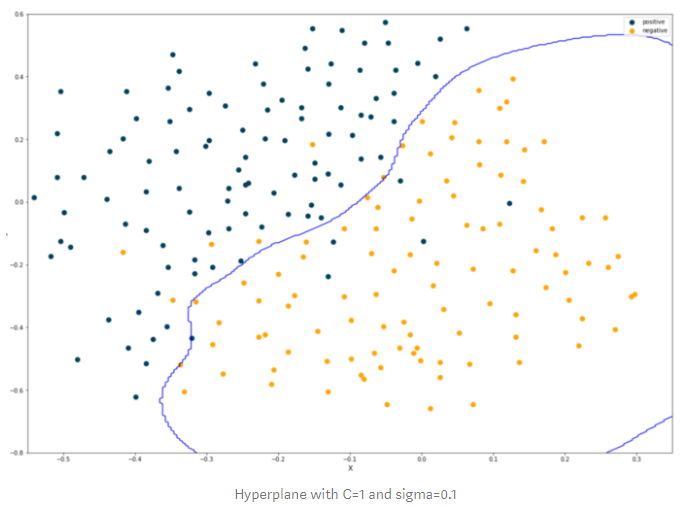
选择最优参数的模型(C=1,sigma=0.1)来预测和画出分类边界:

结果图:
项目4——用SVM进行垃圾邮件分类
下载数据,并用线性核进行分类,得到训练准确率和测试准确率。
代码如下:

得到训练准确率和测试准确率的结果分别为:99.8%和98.9%。
本文介绍了最大间隔分类器的原理,若遇到非线性边界数据的分类任务,则需要用支持向量机去构建模型。文章通过四个小项目解释线性核SVM,高斯核SVM,正则化参数C的作用以及如何用交叉验证方法选择模型的最优参数。
往期精彩回顾
本站qq群851320808,加入微信群请扫码:
