机器学习基础篇：支持向量机（SVM）理论与实践-技术圈

编译 | AI有道

什么是支持向量机（SVM）？

支持向量机 (SVM) 是一种相对简单的监督机器学习算法，用于解决分类或回归问题。它更适合分类，但有时对回归也非常有用。SVM算法的本质是在不同的数据类型之间找到一个超平面来创建边界。在二维空间中，这个超平面是一条直线。

在 SVM算法中，我们在 N 维空间中绘制数据集中的每个数据项，其中 N 是数据中特征/属性的数量。接下来，我们找到最佳的超平面来对不同类型的数据进行分类。因此我们可以了解到SVM 本质上只能解决二分类的问题（即，在两个类之间进行选择）。但是，如今有多种技术可用于解决多分类的问题。

支持向量机（SVM）解决多分类问题

为了在多分类问题上使用SVM，我们可以为每一类数据创建一个二元分类器。每个分类器的两个结果将是：

数据点属于该类或
数据点不属于该类或

例如，在水果分类问题中，要进行多类分类，我们可以为每个水果创建一个二元分类器。例如，“芒果”类，将有一个二元分类器来预测它是芒果还是不是芒果。选择得分最高的分类器作为 SVM 的输出。

复杂的 SVM（非线性可分）

SVM对线性可分数据进行分类有比较好的表现。线性可分数据是任何可以绘制在图形中并且可以使用直线进行分类的数据。

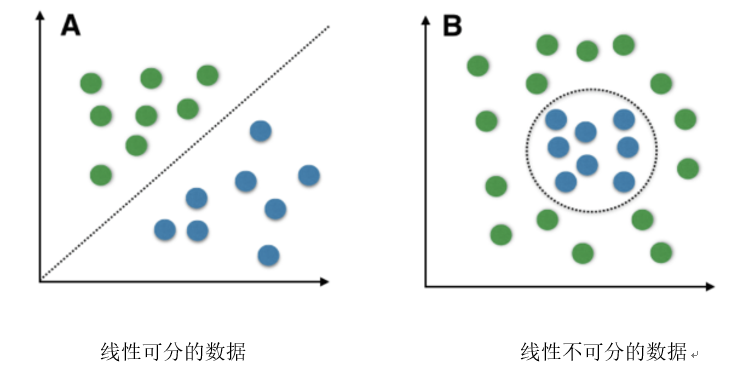
我们使用带内核的SVM 来处理非线性可分的数据。比如说，我们把一维非线性可分的数据可以转换为二维数据，该数据将将在二维上线性可分。这是通过将每个一维数据点映射到相应的二维有序对来完成的。

因此，对于任何维度的任何非线性可分数据，我们可以将数据映射到更高的维度，然后使其变得线性可分。这是一个非常强大和普遍的转变。

内核不是数据点之间相似性的度量。核化 SVM 中的核函数告诉您，给定原始特征空间中的两个数据点，新变换的特征空间中的点之间的相似度是多少。

现有各种可用的内核函数，其中两个比较流行：

Radial BasisFunction Kernel (RBF)：变换后的特征空间中两点之间的相似度是向量与原始输入空间之间距离的指数衰减函数，如下所示。RBF 是 SVM 中使用的默认内核。

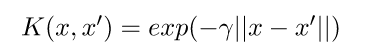
多项式内核：多项式内核采用一个附加参数“度”来控制模型的复杂度和转换的计算成本。

内核化 SVM 的优点：

1、在有些数据集上表现的比较常好；

2、具有通用性：可以指定不同的内核函数，或者也可以为特定数据类型定义自定义内核；

3、同样适用于高维数据和低维数据。

内核化 SVM 的缺点：

1、效率（运行时间和内存使用）随着训练集大小的增加而降低；

2、需要标准化输入数据和参数调整，自适应能力弱；

3、没用提供概率估计方法；

4、对做出的预测比较难解释。

用python语言实现SVM

首先我们用sklearn包自带的方法创建两组数据集：

# importing scikit learn with make_blobsfrom sklearn.datasets.samples_generator import make_blobs
# creating datasets X contarining n_samples# Y containing two classesX,Y = make_blobs(n_samples=500, centers=2,          random_state=0, cluster_std=0.40)import matplotlib.pyplot as plt# plotting scattersplt.scatter(X[:,0], X[:, 1], c=Y, s=50, cmap='spring');plt.show()

创建后的数据集可视化如下图：

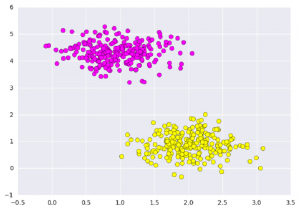
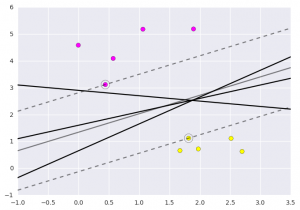
SVM不仅是在此处在两个类之间画一条线，而且还要考虑某个给定宽度的线周围的区域。下面是它的外观示例：

# creating line space between -1 to 3.5 xfit = np.linspace(-1, 3.5)
# plotting scatterplt.scatter(X[:, 0], X[:, 1], c=Y, s=50, cmap='spring')
# plot a line between the different sets of datafor m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:    yfit = m * xfit + b    plt.plot(xfit, yfit, '-k')    plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',     color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);plt.show()

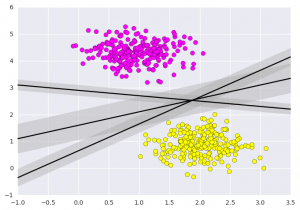
以上是支持向量机的直觉，它优化了表示数据集之间垂直距离的线性判别模型。现在让我们使用我们的训练数据训练分类器。在训练之前，我们需要将癌症数据集导入为 csv 文件，我们将从所有特征中训练两个特征。

# importing required librariesimport numpy as npimport pandas as pdimport matplotlib.pyplot as plt
# reading csv file and extracting class column to y.x = pd.read_csv("C:\...\cancer.csv")a = np.array(x)y  = a[:,30] # classes having 0 and 1
# extracting two featuresx = np.column_stack((x.malignant,x.benign))
# 569 samples and 2 featuresx.shape 
print (x),(y)

现在我们将利用这些点来拟合SVM分类器。虽然似然模型的数学细节很有趣，但我们将在别处阅读这些细节。相反，我们只是将scikit-learn 算法视为完成上述任务的黑匣子。

# import support vector classifier # "Support Vector Classifier"from sklearn.svm import SVC  clf = SVC(kernel='linear') 
# fitting x samples and y classes clf.fit(x, y)

拟合完成后，该模型可用于预测新值：

clf.predict([[120, 990]])
clf.predict([[85, 550]])

输出：

array([ 0.])

array([ 1.])

我们可以通过 matplotlib 分析获取的数据和预处理方法以制作最佳超平面的过程。

原文链接：

https://www.geeksforgeeks.org/introduction-to-support-vector-machines-svm/

仅用于学术分享，版权属于原作者。

若有侵权，请联系微信号:yiyang-sy 删除或修改！

—THE END—