【机器学习基础】数学推导+纯Python实现机器学习算法10：线性不可分支持向量机-技术圈

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

本节笔者和大家讨论支持向量机的最后一种情况——非线性支持向量机。前面两节我们探讨了数据样例是完全线性可分情况和近似线性可分情况下的支持向量机模型。但线性可分情况并非总如人愿，大多数时候我们遇到的都是非线性情况。

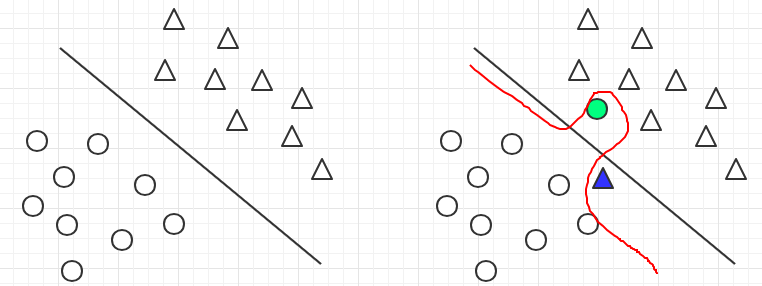
所谓非线性可分问题，就是对于给定数据集，如果能用一个超曲面将正负实例正确分开，则这个问题为非线性可分问题。非线性问题的一个关键在于将原始数据空间转换到一个新的数据空间，在原始空间中的非线性可分问题到新空间就是是线性可分问题。

一般来说，用线性可分方法来解决非线性可分问题可分为两步：首先用一个变换将原始空间的数据映射到新空间，再在新空间中用线性分类学习方法训练分类模型。这种将原始空间转换到新空间的方法称为核技巧(kernel trick)。

假设存在一个从输入空间到特征空间的映射，使得所有的x和z都有函数K(x,z)=&(x).&(z)，则称K(x,z)为核函数。在实际问题中，通常直接给定核函数的形式，然后进行求解。核函数的选择通常依赖于领域知识，最后由实验验证其有效性。常用的核函数包括多项式核函数、高斯核函数以及sigmoid核函数等，核函数更多细节问题可参考统计学习方法。

基于核函数的非线性支持向量机对偶优化问题如下：

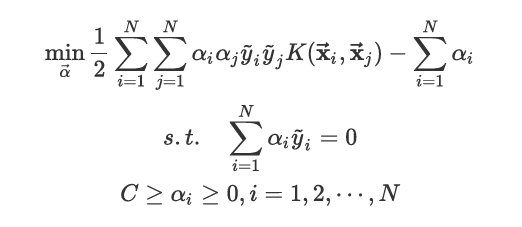
当核函数为正定核的时候，上述优化问题为凸优化问题，是可以直接进行求解的。可求得最优解：

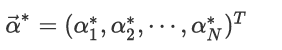
计算w如下：

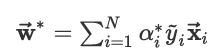
最后可构造分类决策函数：

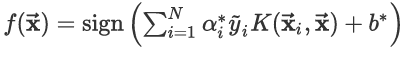
虽然凸优化问题可以直接求解，但当数据量很大时，直接求解将会非常低效，这时候可能需要一些高效的训练算法，比如说SMO(序列最小最优化)算法。关于SMO算法的内容这里不展开叙述，可参考统计学习方法了解更多内容。

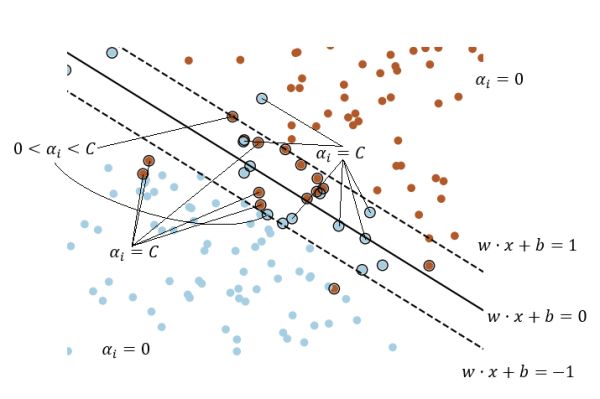
下面来看基于cvxopt的非线性支持向量机快速实现方法。

导入相关package：

import numpy as npfrom numpy import linalgimport cvxoptimport cvxopt.solversimport pylab as pl

定义多项式核函数如下：

def polynomial_kernel(x, y, p=3):    return (1 + np.dot(x, y)) ** p

生成示例数据：

def gen_non_lin_separable_data():    mean1 = [-1, 2]    mean2 = [1, -1]    mean3 = [4, -4]    mean4 = [-4, 4]    cov = [[1.0, 0.8], [0.8, 1.0]]    X1 = np.random.multivariate_normal(mean1, cov, 50)    X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50)))    y1 = np.ones(len(X1))    X2 = np.random.multivariate_normal(mean2, cov, 50)    X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50)))    y2 = np.ones(len(X2)) * -1    return X1, y1, X2, y2

然后是构建非线性支持向量机模型，完整版代码如下：

import numpy as npfrom numpy import linalgimport cvxoptimport cvxopt.solvers
def polynomial_kernel(x, y, p=3):    return (1 + np.dot(x, y)) ** p
class nolinear_svm(object):        def __init__(self, kernel=linear_kernel, C=None):        self.kernel = kernel        self.C = C        if self.C is not None: self.C = float(self.C)        def fit(self, X, y):        n_samples, n_features = X.shape                # Gram 矩阵        K = np.zeros((n_samples, n_samples))        for i in range(n_samples):            for j in range(n_samples):                K[i, j] = self.kernel(X[i], X[j])                P = cvxopt.matrix(np.outer(y, y) * K)        q = cvxopt.matrix(np.ones(n_samples) * -1)        A = cvxopt.matrix(y, (1, n_samples))        b = cvxopt.matrix(0.0)                if self.C is None:            G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1))            h = cvxopt.matrix(np.zeros(n_samples))        else:            tmp1 = np.diag(np.ones(n_samples) * -1)            tmp2 = np.identity(n_samples)            G = cvxopt.matrix(np.vstack((tmp1, tmp2)))            tmp1 = np.zeros(n_samples)            tmp2 = np.ones(n_samples) * self.C            h = cvxopt.matrix(np.hstack((tmp1, tmp2)))                # 求解二次规划        solution = cvxopt.solvers.qp(P, q, G, h, A, b)                # 获得拉格朗日乘子        a = np.ravel(solution['x'])                # 非零拉格朗日乘子的支持向量        sv = a > 1e-5        ind = np.arange(len(a))[sv]        self.a = a[sv]        self.sv = X[sv]        self.sv_y = y[sv]        print("%d support vectors out of %d points" % (len(self.a), n_samples))                # 截距项        self.b = 0        for n in range(len(self.a)):            self.b += self.sv_y[n]            self.b -= np.sum(self.a * self.sv_y * K[ind[n], sv])        self.b /= len(self.a)                # 权重参数向量        if self.kernel == linear_kernel:            self.w = np.zeros(n_features)            for n in range(len(self.a)):                self.w += self.a[n] * self.sv_y[n] * self.sv[n]        else:            self.w = None                # 预测函数    def project(self, X):        if self.w is not None:            return np.dot(X, self.w) + self.b        else:            y_predict = np.zeros(len(X))            for i in range(len(X)):                s = 0                for a, sv_y, sv in zip(self.a, self.sv_y, self.sv):                    s += a * sv_y * self.kernel(X[i], sv)                y_predict[i] = s            return y_predict + self.b        def predict(self, X):        return np.sign(self.project(X))

if __name__ == "__main__":    def gen_non_lin_separable_data():        mean1 = [-1, 2]        mean2 = [1, -1]        mean3 = [4, -4]        mean4 = [-4, 4]        cov = [[1.0, 0.8], [0.8, 1.0]]        X1 = np.random.multivariate_normal(mean1, cov, 50)        X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50)))        y1 = np.ones(len(X1))        X2 = np.random.multivariate_normal(mean2, cov, 50)        X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50)))        y2 = np.ones(len(X2)) * -1        return X1, y1, X2, y2        def split_train(X1, y1, X2, y2):        X1_train = X1[:90]        y1_train = y1[:90]        X2_train = X2[:90]        y2_train = y2[:90]        X_train = np.vstack((X1_train, X2_train))        y_train = np.hstack((y1_train, y2_train))        return X_train, y_train        def split_test(X1, y1, X2, y2):        X1_test = X1[90:]        y1_test = y1[90:]        X2_test = X2[90:]        y2_test = y2[90:]        X_test = np.vstack((X1_test, X2_test))        y_test = np.hstack((y1_test, y2_test))        return X_test, y_test        def plot_margin(X1_train, X2_train, clf):        def f(x, w, b, c=0):            return (-w[0] * x - b + c) / w[1]                pl.plot(X1_train[:, 0], X1_train[:, 1], "ro")        pl.plot(X2_train[:, 0], X2_train[:, 1], "bo")        pl.scatter(clf.sv[:, 0], clf.sv[:, 1], s=100, c="g")                # w.x + b = 0        a0 = -4;        a1 = f(a0, clf.w, clf.b)        b0 = 4;        b1 = f(b0, clf.w, clf.b)        pl.plot([a0, b0], [a1, b1], "k")                # w.x + b = 1        a0 = -4;        a1 = f(a0, clf.w, clf.b, 1)        b0 = 4;        b1 = f(b0, clf.w, clf.b, 1)        pl.plot([a0, b0], [a1, b1], "k--")                # w.x + b = -1        a0 = -4;        a1 = f(a0, clf.w, clf.b, -1)        b0 = 4;        b1 = f(b0, clf.w, clf.b, -1)        pl.plot([a0, b0], [a1, b1], "k--")                pl.axis("tight")        pl.show()            def plot_contour(X1_train, X2_train, clf):        pl.plot(X1_train[:, 0], X1_train[:, 1], "ro")        pl.plot(X2_train[:, 0], X2_train[:, 1], "bo")        pl.scatter(clf.sv[:, 0], clf.sv[:, 1], s=100, c="g")                X1, X2 = np.meshgrid(np.linspace(-6, 6, 50), np.linspace(-6, 6, 50))        X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))])        Z = clf.project(X).reshape(X1.shape)        pl.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')        pl.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower')        pl.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower')                pl.axis("tight")        pl.show()        def test_non_linear():        X1, y1, X2, y2 = gen_non_lin_separable_data()        X_train, y_train = split_train(X1, y1, X2, y2)        X_test, y_test = split_test(X1, y1, X2, y2)                clf = nolinear_svm(polynomial_kernel)        clf.fit(X_train, y_train)                y_predict = clf.predict(X_test)        correct = np.sum(y_predict == y_test)        print("%d out of %d predictions correct" % (correct, len(y_predict)))                plot_contour(X_train[y_train == 1], X_train[y_train == -1], clf)        test_non_linear()

基于多项式核函数的非线性支持向量机分类效果如下：

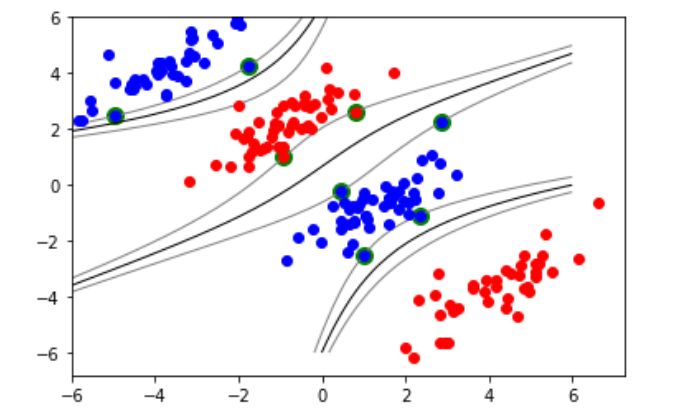
以上就是本节内容，关于支持向量机的部分内容，笔者就简单写到这里，下一讲我们来看看朴素贝叶斯算法。完整代码文件和数据可参考笔者GitHub地址：

https://github.com/luwill/machine-learning-code-writing

好消息！
小白学视觉知识星球
开始面向外开放啦👇👇👇



下载1：OpenCV-Contrib扩展模块中文版教程
在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~