探究Integral Pose Regression性能不足的原因

论文标题：Removing the Bias of Integral Pose Regression

论文链接：Removing the Bias of Integral Pose Regression (thecvf.com)

补充材料链接：Gu_Removing_the_Bias_ICCV_2021_supplemental.pdf (thecvf.com)

小伙伴介绍的一篇ICCV 2021的文章，作者深入分析了Integral Pose Regression的问题，并提出了一个解决方案，虽然没有提出什么fancy的结构，却能让我们对于过去习以为常的做法更加深入理解，我个人很喜欢这种性质的文章。本文实验相当翔实，从不同角度对Heatmp和Regression方法的优劣进行了探索，其中很多结论都让我获益匪浅。

并且，由于本文提出的方法足够简单，所以在理解后根本不需要开源就能很容易加入到我们的代码中使用。

0. 前言

Integral Pose Regression是DSNT方法提出来以后一个较为完整的实验工作，不仅将DSNT在各个数据集上的实验补齐，还利用DSNT的特性进一步扩展到了3D任务上，让2D和3D数据可以联合训练。

所谓DSNT，或者说Integral Pose Regression方法，其实就是对特征图进行归一化后求期望来获得坐标值的方法，是对Heatmap-based方法后处理时Argmax不可导问题的一个解决方案，将Argmax软化为可微分的Soft-Argmax，进而实现了端到端训练，使得坐标值可以直接监督网络训练。

更多的细节我在Sampling-Argmax这篇文章中进行了详细介绍，有兴趣的小伙伴可以前往阅读。

在本文的工作中，作者将Heatmap-based方法总结为一种检测任务：网络输出的是二维平面上的概率分布，在标准的做法里，这个概率分布图的解码方式是通过Argmax操作来进行的：

由于Argmax操作不可导，使得训练无法端到端进行，网络的输出还需要进行后处理，于是Integral Pose Regression通过Soft-Argmax替换了Argmax，通常来说，会对网络输出的Heatmap经过一次Softmax归一化，然后计算期望：

需要注意的是，一般我们常用的softmax是没有使用参数 的，它可以起到平滑作用，越小时softmax的结果越“扁平”，越大则结果越“尖锐”，正常情况下，我们默认取所以没有写出来。

1. Softmax的问题

一般来说，Softmax后计算期望，能够得到一个非常近似Argmax的值，这是一个很自然的过程，而且更妙的是，由于期望并不一定是整数，Soft-Argmax甚至能避开Argmax方法由于输出特征图尺寸过小带来的量化误差影响，这听上去很美好。

然而大家都知道的现实是Soft-Argmax方法虽然确实在小分辨率特征图输出上，能略胜Heatmap方法一筹，但一旦输出分辨率够高，性能就远远不如了。

那么我们很自然地就要问一句，为什么？

本文揭示了Softmax的一个性质：倾向于让每一项的值都非零。简单来说，对于一个非常尖锐的分布（比如one-hot），Softmax会将其软化，变成一个渐变的分布，也就是说，原本取值为0的项，会被Softmax赋上一个非零的值，尽管这个值也许非常小，非常接近于0，但它是非零的。

从图像上来看，概率分布图会出现一个长长的非零的尾巴。 而当我们计算概率分布的期望时，这些原本为0，现在非零的项，就都会为期望值的计算“贡献自己的一份力”（os：大可不必）

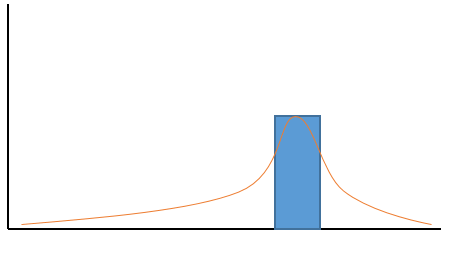
那么，很自然地，输入特征图上响应值的大小，就会对Softmax的结果起到影响了，因为假如响应值是一个接近0的数字，那么Softmax之后的分布，原本为0的项，跟非0项的值会非常接近。

这个性质导致的结果是，最后计算得到的期望值会不准确。只有响应值足够大，分布足够尖锐的时候，期望值才接近Argmax结果，一旦响应值小，分布平缓，期望值会趋近于中心位置。

这里我用一段简单的代码来实验：

# 定义一个一维的长度为10的分布
a = torch.zeros((10, ))

# 在第8项上设置响应
target_idx = 8
a[target_idx] = 10
print('dist:\n', a)

# 进行softmax归一化
softmax_res = a.softmax(0)
print('after softmax:\n', softmax_res)

# 求期望值
lin = torch.tensor([x for x in range(10)])
expectation = (lin * softmax_res).sum()
print('expectation:\n', expectation)

dist:
 tensor([ 0., 0., 0., 0., 0., 0., 0., 0., 10., 0.]) 

after softmax:
 tensor([4.5381e-05, 4.5381e-05, 4.5381e-05, 4.5381e-05, 4.5381e-05, 4.5381e-05, 4.5381e-05, 4.5381e-05, 9.9959e-01, 4.5381e-05])

expectation:
 tensor(7.9984)

可以看到，当响应值取10时，估计的期望值为7.998，是非常接近8的。

但假如我们把响应值改为1：

# 定义一个一维的长度为10的分布
a = torch.zeros((10, ))

# 在第8项上设置响应
target_idx = 8
a[target_idx] = 1
print('dist:\n', a)

# 进行softmax归一化
softmax_res = a.softmax(0)
print('after softmax:\n', softmax_res)

# 求期望值
lin = torch.tensor([x for x in range(10)])
expectation = (lin * softmax_res).sum()
print('expectation:\n', expectation)

dist:
 tensor([0., 0., 0., 0., 0., 0., 0., 0., 1., 0.]) 

after softmax:
 tensor([0.0853, 0.0853, 0.0853, 0.0853, 0.0853, 0.0853, 0.0853, 0.0853, 0.2320, 0.0853])

expectation:
 tensor(5.0132)

期望值顿时就不尽如人意了。

更进一步讲，这里的“尖锐”与否，实际上是与分布的长度相关的，这很好理解，某个高楼大厦放在某个地区来看，它是高楼，但如果是用中国地图来看，它也许只是一个不起眼的小突起了。Softmax的性质会把它原本突起的力量发散给所有的非零项，所以输出特征图分辨率越大的时候，所需要的响应强度也越大，否则期望值就可能因为“响应不够强”而趋近于中央。

2. naive solution

在发现Softmax这个性质后，作者先想到了一个朴素的解决方案，也就是我们上面专门提到的，通过调整，我们可以控制Softmax输出的分布的尖锐与否，只要足够大，是能够让期望估计值重新回到准确的。

本文实验可视化如下：

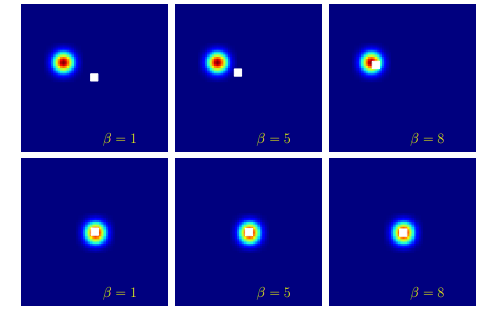
图中的圆圈为特征图响应值，白色的点为计算得到的期望值，可以看到随着增大，期望值逐渐去到了响应值最大点。

然而问题当然不会这么简单，取值越来越大，当趋近无穷大时，Softmax就会收敛到Argmax形式，函数就变成不可导了。并且，随着它增大，远离中心点的像素上的梯度也会变小，直到消失。 因此在实际应用中，我们不得不进行trade-off，并且这个最优的参数值很难把握。

于是本文又继续思考新的解决方案。

3. Bias Compensation

我们其实已经定位了问题根源所在，Soft-Argmax方法不准是因为响应值不够大时，期望值趋近于中央，而期望值趋近于中央的原因在于，Softmax后出现的那条多余的长长的尾巴，更气人的是，这个尾巴通过只能尽可能地缩小，无法消除，甚至在这个过程中还会产生副作用（回传导数消失）。

那么，我们是不是可以换个思路，既然这个尾巴消除不了，我们干脆把它求出来，然后从结果期望值里减去，这不就相当于“切掉”了这个尾巴吗？

具体而言，假设响应值是符合高斯分布的，我们可以根据响应最大值点两倍的宽度，把特征图划分成四个区域：

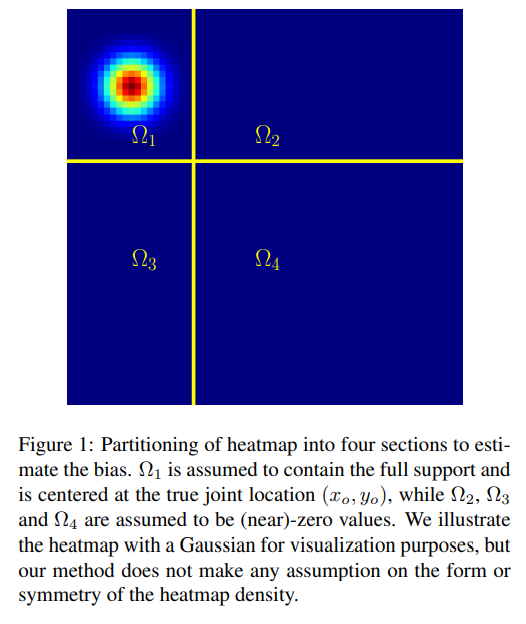
我们知道一旦经过Softmax，原本都是0值的2、3、4象限区域瞬间就会被长长的尾巴填满，而对于第1象限区域，由于响应值正处于区域的中央，因此不论响应值大小，该区域的估计期望值都会是准确的。

让我们回到Softmax公式：

为了简洁，我们先把分母部分用C来表示：

由于假设2、3、4区域的响应值都为0，因而分子部分计算出来为1，划分区域后的Softmax结果可以表示成：

然后继续按照Soft-Argmax的计算公式带入，期望值的计算可以表示为：

即：第一区域的期望值，加上另外三个区域的期望值。

已知2、3、4区域，因此这三个区域的期望值可以把提出来，只剩下

而这里的求和，在几何意义上等价于该区域的中心点坐标乘以该区域的面积，我给一个简单的演示，对于[n, m]区间：

因而对于整块特征图的期望值，又可以看成四个区域中心点坐标的加权和：

由于四个区域的中心点存在对称性，假设第一区域中心点坐标为，那么剩下三个区域中心点坐标为

对应上面我们得出的乘以中心点坐标乘以面积，就得到了每个加权值：

带入上面的加权和公式(6)，整张特征图的期望值可以表示为：

由于已知四个区域权重相加为1，所以有 ，因此整张特征图期望值化简成如下形式：

由于值可以很容易通过对整张图计算Soft-Argmax得到，因此对公式(9)移项就能得到准确的第一区域中心点坐标：

这一步就相当于将原本多余的长尾从期望值中减去了，对该公式我们还可以进一步分析，整张图的期望估计值相当于第一区域期望值的一个偏移，当C足够大时，和是趋近于相等的。

又因为C中是包含的，因此我们最初通过来优化结果的本质其实也是在调节C的大小：

另外我们可以发现，公式(10)是与区域位置无关的，并且不需要用到任何的Gound Truth信息，因此不论是训练还是推理阶段，都可以直接计算准确的坐标值。

至此，本文最核心的方法就介绍完了。

4.实验结果

经过实验可以看到，本文提出的方法对于Integral Pose Regression有显著提升，能追平甚至超越Heatmap-based方法：

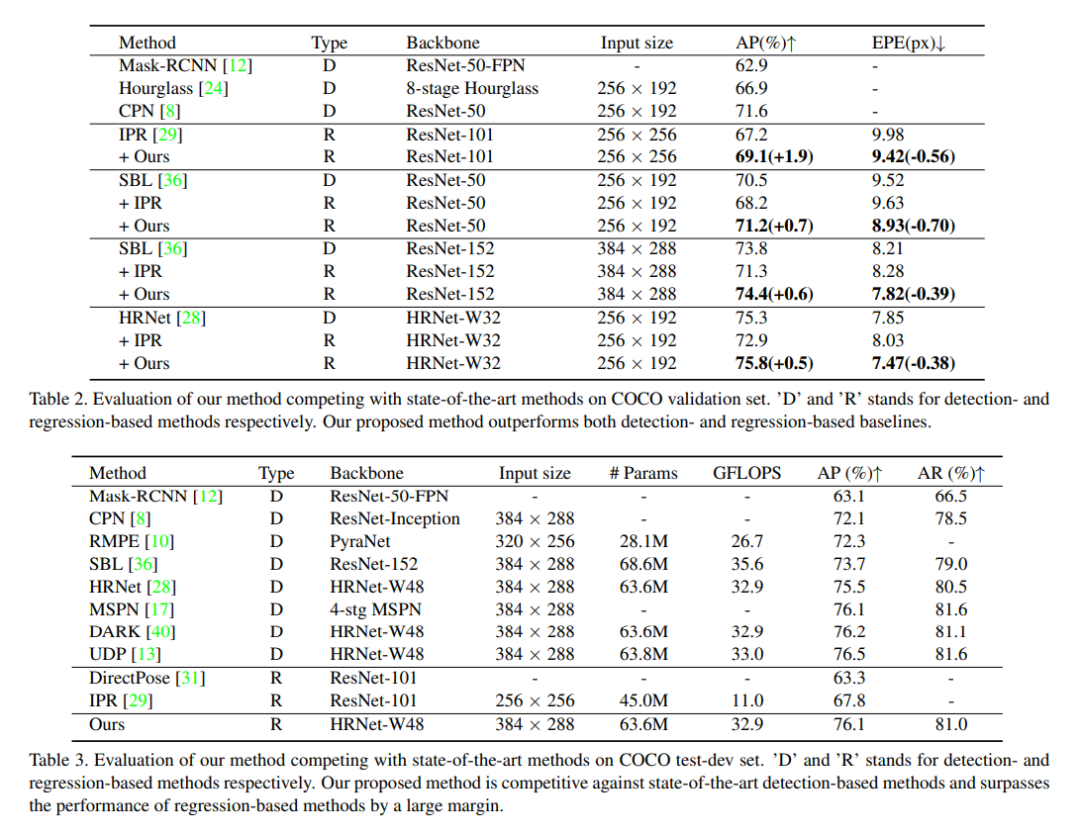
本文做的其他几个实验我觉得是比较有意思的，很值得我们关注。

本文对数据集进行了进一步的精细化分，按照关键点个数、遮挡率、输入尺寸等多个角度来评估不同方法的表现，这是非常科学且严谨的，能帮助我们看清不同方法的优势和劣势。

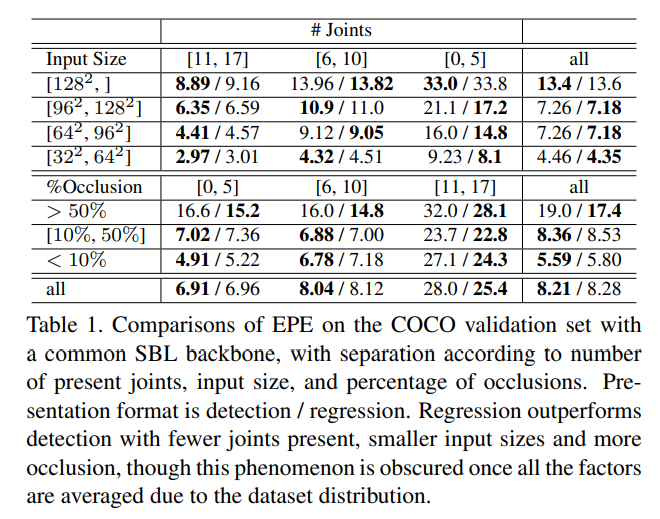
从该实验结果我们可以得出以下结论：

1. Heatmap-based方法在输入尺寸大、遮挡少的情况下表现更佳
2. Regression-based方法在输入尺寸小、遮挡多的情况表现更佳
3. 当对象被画面截断时，画面中出现的关键点数少时，Heatmap-based方法更有优势

加入本文提出的修正方法后，在任何情况下模型均能取得更好的表现：

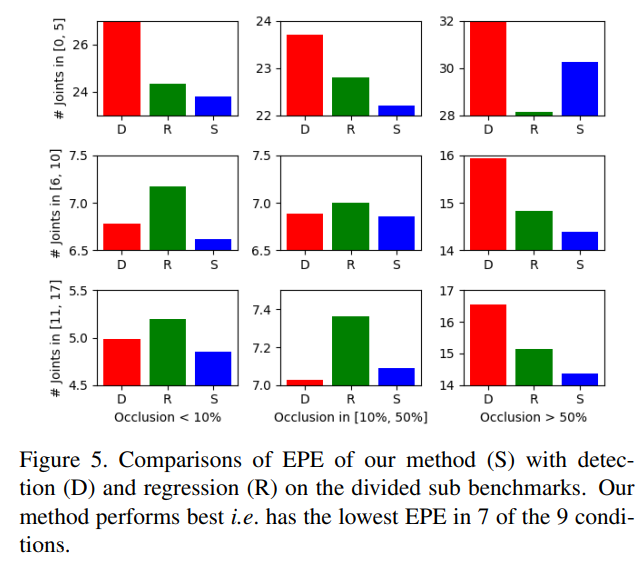
关于Heatmap和Regression不同的监督方式对于训练速度的影响，本文也进行了实验探索：

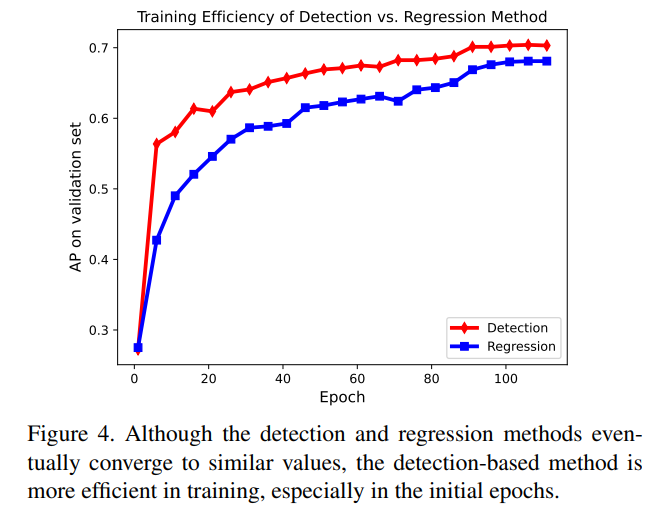
首先是可以观察到，尽管两种方法最终取得的精度相差不大，但训练效率上却有显著差异，Heatmap监督的方法在训练初期提升非常迅速。本文分析其原因在于，Heatmap的监督信息非常明确，而Regression方法由于只依赖期望值的监督，对概率分布的性质没有约束，因此存在歧义性影响了模型学习，这部分的结论在我之前介绍的Sampling-Argmax文章中进行了深入分析，并且提出了更优的解决方案。

随后本文提出了一种监督策略，将两种监督信息进行了混合，Heatmap作为辅助loss，并随着训练的进行逐渐降低其权重：

实验结果如下：

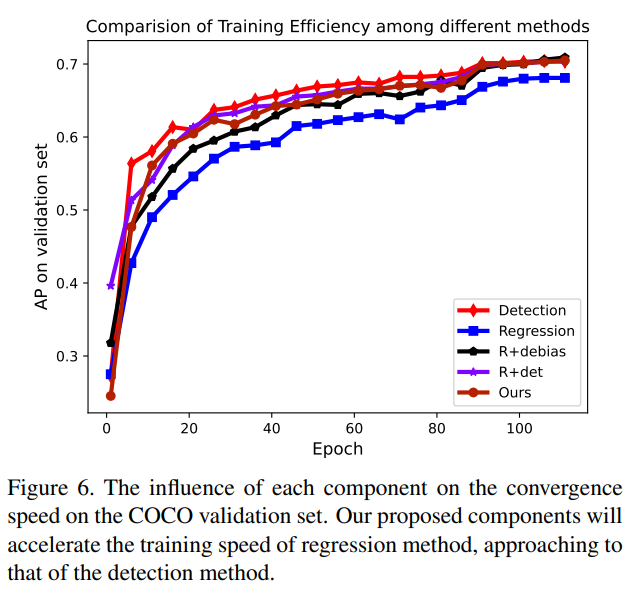
另外一个合适的值在本文的方法基础上还能带来进一步的收益：

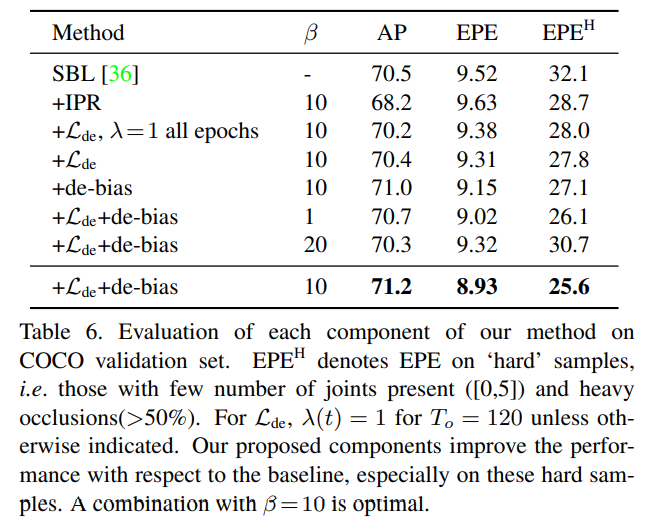
而的使用也非常简单，只需要对代码做一点点修改：

x = x.softmax() # original
x = (10 * x).softmax() # new

5. 结语

本文深入分析了Softmax的性质，找到了其中的问题，挖掘出Soft-Argmax方法性能不足的原因，并通过数学方式进行了修正，使得Regression方法获得了巨大的性能提升，并且做了大量的实验来对比分析，为我们自己的模型训练提供了可以参考的经验，我认为是一篇非常优秀的工作。

声明：转载请说明出处