使用逻辑回归预测用户是否会购买SUV-技术圈

往期推荐

机器学习100天学习计划 — 第1天数据预处理

机器学习100天学习计划 — 第2天线性回归

机器学习100天学习计划 — 第3天多元线性回归

这是机器学习100天学习计划的第4天，我们将探讨逻辑回归存在的必要性、逻辑回归训练时的数据要求、逻辑回归的基本运行原理。

文章的最后我们会做一个简单应用：使用逻辑回归预测用户是否会购买SUV.

为什么需要逻辑回归？

从前面的学习中知道，线性回归对数据的要求非常严格，比如自变脸必须满足正态分布，特征之间的多重共线性需要消除，实际生活中的数据无法彻底满足这些要求，因此它在现实场景中的应用效果有限。

为了解决那些不满足线性回归的严格要求的数据分析需求，我们需要逻辑回归。

逻辑回归由线性回归变化而来，它对数据的要求没那么高，分类效力很强，对数据不需要做消除多重共线性之类的预处理。逻辑回归有以下三个优点：

1.逻辑回归对线性关系的拟合效果好到丧心病狂，比如电商营销预测、信用卡欺诈、打分等实际落地应用相关的数据都是逻辑回归的强项。

2.对于线性数据，逻辑回归的拟合和计算非常快，尤其对于大数据，这点优势极其明显。

3.逻辑回归返回的分类结果不是固定的0或1，而是以小数形式反馈的类概率数字，因此你可以把逻辑回归返回的结果当成连续型数据使用。

逻辑回归的原理不简单，细节非常多，不是在本篇文章能讲完的，所以本篇文章主要是给大家提供逻辑回归的使用方法及其注意事项，并以一个小应用为例入门逻辑回归。

逻辑回归数据要求

逻辑回归对数据并不是没有要求，下面就是使用逻辑回归分析前需要注意的几个问题：

1.样本数量最好大于300.

2.自变量最好是“分类”的形式。

3.模型运行前去除异常值和缺失值。

你并不需要严格遵守上述要求，遇到特殊情况可以灵活变通。

逻辑回归如何工作

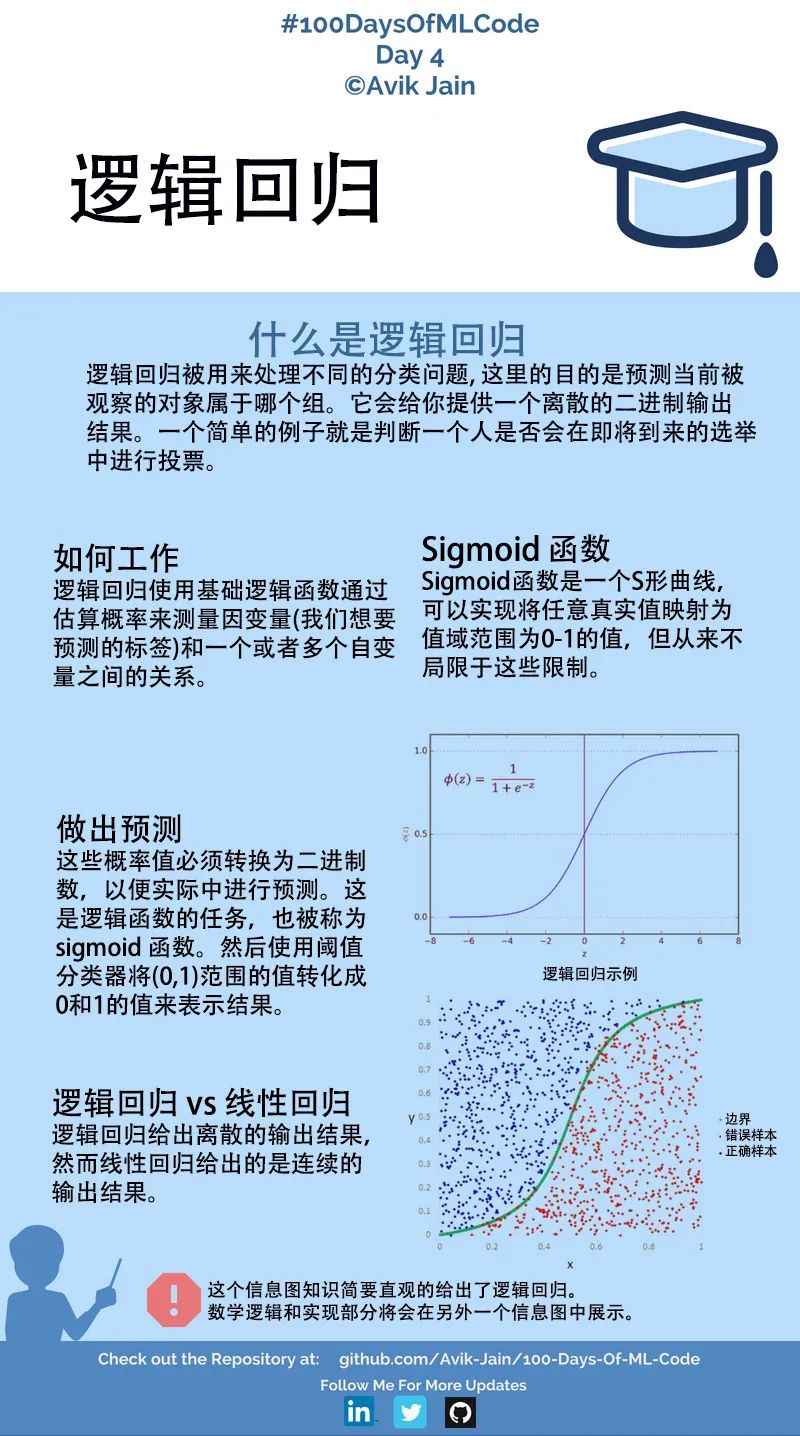
上述内容可能你不一定能看得懂，没关系，往后看我们的实操训练，动手实操后你一定有所收获。

预测用户是否会购买SUV

现在有一个数据集包含了社交网络中用户的信息。这些信息涉及用户ID,性别,年龄以及预估薪资。一家汽车公司刚刚推出了他们新型的豪华SUV，我们尝试预测哪些用户会购买这种全新SUV。并且在最后一列用来表示用户是否购买:

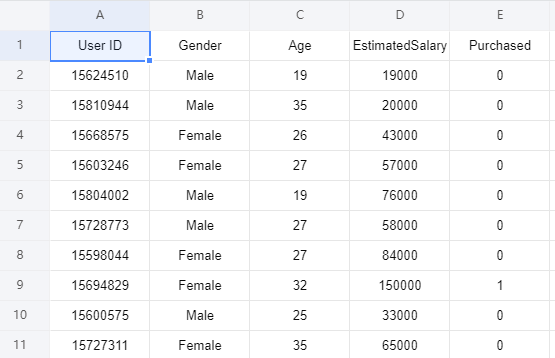
接下来我们将建立一种逻辑回归模型来预测用户是否购买这种SUV，该模型基于两个变量，分别是年龄和预计薪资。因此我们的特征矩阵将是这两列。我们尝试寻找用户年龄与预估薪资之间的某种相关性，以及他是否购买SUV的决定。

本文数据集和源代码可在Python实用宝典公众号后台回复：机器学习4 下载。

4.1

数据预处理

导入库：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

导入数据集，为了方便可视化，我们暂时去除了性别这一列：

dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
Y = dataset.iloc[:,4].values

将数据集分成训练集和测试集：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.25, random_state = 0)

特征缩放：

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

4.2

逻辑回归模型

逻辑回归是一个线性分类器，这意味着我们在二维空间中，我们两类用户（购买和不购买）将被一条直线分割。

将逻辑回归应用于训练集：

from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
classifier.fit(X_train, y_train)

4.3

预测

预测测试集结果：

y_pred = classifier.predict(X_test)

4.4

模型评估

刚刚我们预测了测试集。现在我们将评估逻辑回归模型是否正确的学习和理解数据。我们将用到混淆矩阵：

混淆矩阵是一种可视化工具，矩阵的每一列代表一个类的实例预测，而每一行表示一个实际的类的实例。之所以如此命名，是因为通过这个矩阵可以方便地看出机器是否将两个不同的类混淆了。

生成混淆矩阵：

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print(cm)

结果如下：

[[65  3]
 [ 8 24]]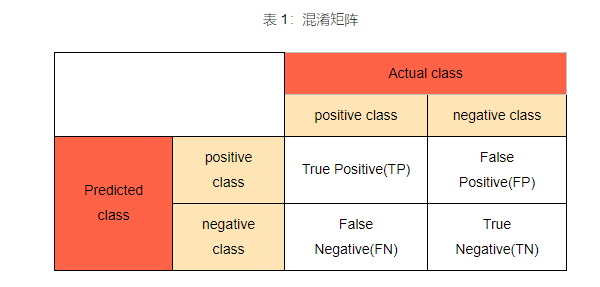

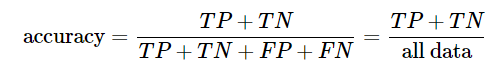
这说明，分类正确的值有65+24=89个，分类错误的值有3+8=11个，准确率为89%.

可视化的代码如下：

上滑查看更多代码

X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
                      np.arange(start=X_set[:, 1].min()-1, stop=X_set[:, 1].max()+1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)

plt.title('LOGISTIC(Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
                      np.arange(start=X_set[:, 1].min()-1, stop=X_set[:, 1].max()+1, step=0.01))

plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)

plt.title('LOGISTIC(Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()

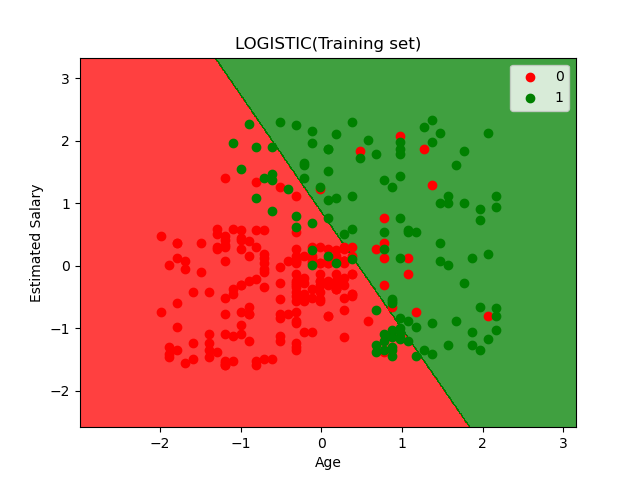
对于训练集，我们训练得到的分隔线如上图所示，存在部分的错误分类，但大部分数据点都分类正确。

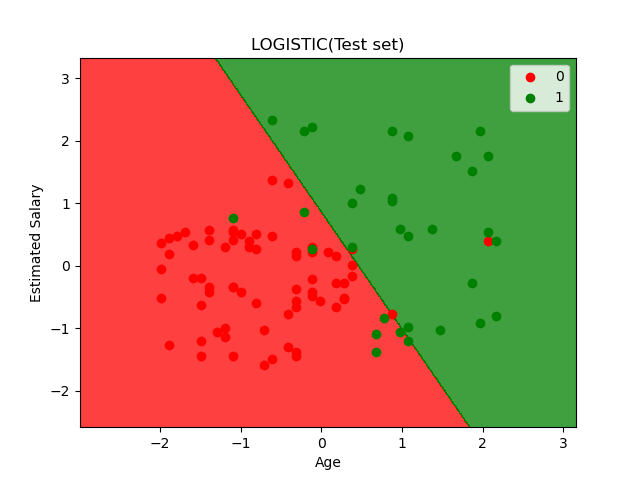
使用训练集得到的分割线来分隔测试集，分类结果如上图所示，有11个错误分类的点。

加上性别一列进行预测

刚刚为了可视化结果，我们去掉了性别这一列进行训练和测试。

但性别对结果的影响是实际存在的，所以我们将性别重新加入训练集中进行训练并测试。

改动非常简单，只需要在导入数据集的时候将性别这一列加回来，并将性别转化为数字：

# 1.导入数据集
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [1, 2, 3]].values
Y = dataset.iloc[:, 4].values

# 性别转化为数字
labelencoder_X = LabelEncoder()
X[:, 0] = labelencoder_X.fit_transform(X[:, 0])

完整代码如下：

上滑查看更多代码

from sklearn.metrics import confusion_matrix
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 1.导入数据集
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [1, 2, 3]].values
Y = dataset.iloc[:, 4].values

# 性别转化为数字
labelencoder_X = LabelEncoder()
X[:, 0] = labelencoder_X.fit_transform(X[:, 0])

# 2.将数据集分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, Y, test_size=0.25, random_state=0)

# 3.特征缩放
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

# 4.训练
classifier = LogisticRegression()
classifier.fit(X_train, y_train)

# 5.预测
y_pred = classifier.predict(X_test)

# 6.评估预测 生成混淆矩阵
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print(cm)

# 生成混淆矩阵
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
print(cm)

结果如下：

(base) G:\push\20210117>python test_with_gender.py
[[65 3]
 [ 7 25]]

可见，分类正确的值有65+25=90个，分类错误的值有3+7=10个，准确率为90%.

这相比于除去性别这一列时得到的89%准确率的测试结果有1%的提升。

我们的文章到此就结束啦，如果你喜欢今天的Python 实战教程，请持续关注Python实用宝典。

有任何问题，可以在公众号后台回复：加群，回答相应红字验证信息，进入互助群询问。

原创不易，希望你能在下面点个赞和在看支持我继续创作，谢谢！

点击下方阅读原文可获得更好的阅读体验

Python实用宝典 (pythondict.com)
不只是一个宝典
欢迎关注公众号：Python实用宝典