干货|简单理解逻辑回归基础
点击上方“小白学视觉”，选择加"星标"或“置顶”
重磅干货，第一时间送达
分类问题其实和回归问题很相似，但是它的输出值y值（也即是说我们打算预测的值）只是少量的一些离散值，像是如果我们只是想要机器通过“观察”某个西瓜的一些特征从而来告诉我们这个西瓜是好是坏，那么我们就可以设输出值y为0表示坏瓜，1表示好瓜，那么判断这个西瓜好坏的过程其实就是一个分类问题，它的输出值就是离散的（仅为0或者1） 。
而分类问题中最简单的是二元分类，顾名思义，就是输出值只有两个，就像上面那个例子，结果只有好瓜和坏瓜，不会输出“不好不坏的”这种莫名其妙的瓜。
在二元分类中，我们常常用0和1来限定y值，继续套用上面那个分瓜的例子，我们假设x(i) 表示西瓜的特征，那么y就被称作西瓜的标签（也就是类别），y的0值往往被称作西瓜的“负类”，1值便称作西瓜的“正类”。有时候我们还会用“+”和“-”来代替1和0，像是在图上的时候，这样会表现的更清楚。
既然分类问题和回归问题的区别仅仅是输出值不同，那么线性回归是不是也能拿来当作分类问题的模型使用呢？就像是那个西瓜，我们如果先用线性回归学习一批好瓜和坏瓜的特征，然后似乎就可以用训练好的模型来预测一个新出现的西瓜是更接近好瓜还是坏瓜了。
这样做确实可以，但得到的结果往往非常不理想。既然我们已经很清楚的知道y要么是0要么是1，就没有必要再用这种吃力不讨好的方式去强行拟合一条回归曲线。但“回归”的假设函数hθ(x)的原理是没有毛病的，因此，我们只需要对原来的线性回归的假设函数做出一些修改:
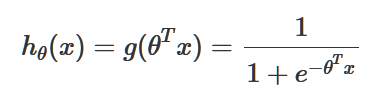
就可以让原来的“回归”曲线变成一条分类曲线。
这里的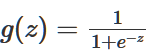
也被叫做逻辑函数或Sigmoid函数，它的图像如下：
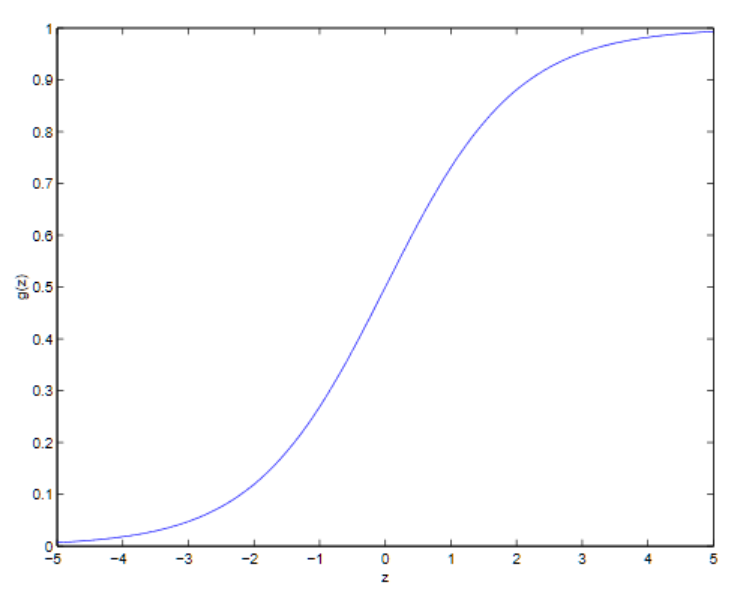
这个时候g(z)在z→∞的时候趋向于1，在z→−∞的时候趋向于0而且除了g(z)，它上面的函数h(x)也被限制在区间(0,1)之间取值。这个sigmoid函数是一个非常神奇的函数，它不仅把输出y映射在了0，1之内，还是一个非常符合“自然”的函数，因为它默认了样本服从高斯分布——太详细的内容我们在之后的“广义生成模型”中讨论，现在讲这个就跑的太远啦。目前的话，我们就先姑且认为我们通过一个神奇的函数把线性回归变成了用于解决分类问题的逻辑回归。
像之前一样，我们让x0=1，可以得到：
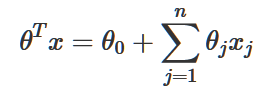
然后，又因为sigmoid函数拥有的优良求导性质：
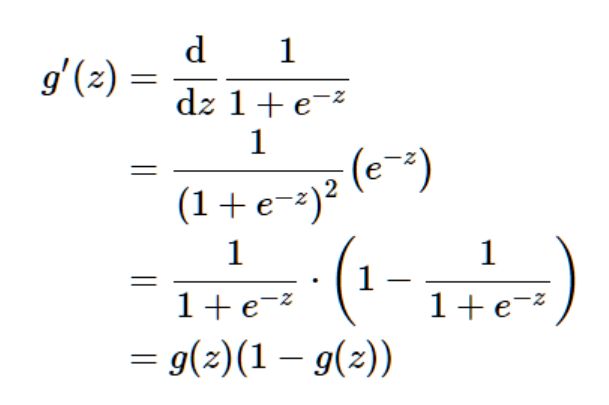
我们就可以利用这个函数来拟合逻辑回归模型了。
根据我们对线性回归应用的在一系列假设的情况下求极大似然的方式，我们可以赋予我们的分类模型一系列概率假设，然后通过最大似然来估计拟合参数。假设：
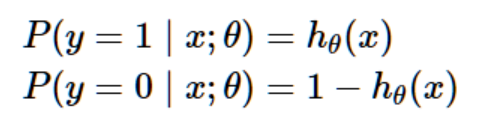
当然，这个两个式子可以合为：
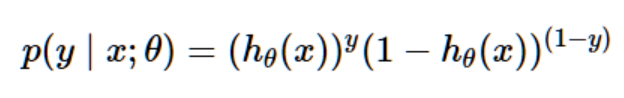
假设训练集中的m个训练样本是相互独立的，我们可以这样写出参数的似然估计：
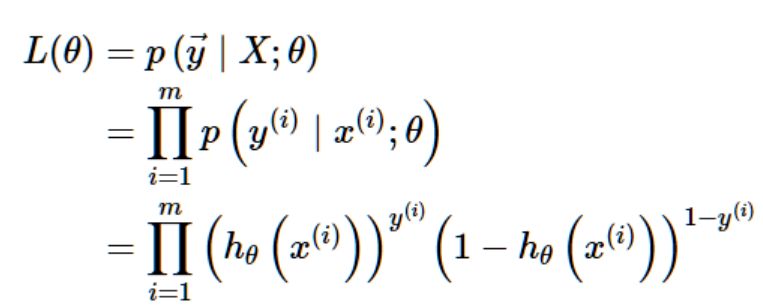
同线性回归中的运算方式一样，我们取对数似然函数：
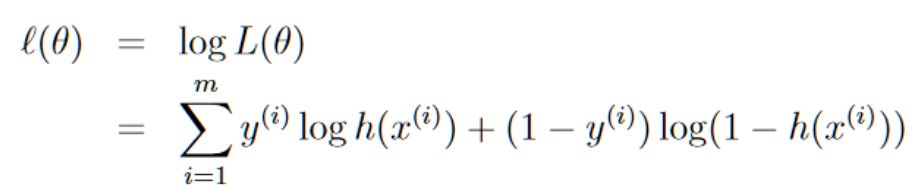
为了让l(θ)取到最大值，我们这次使用梯度上升法，它与梯度下降一样，只不过方向θ要增大，因此，θ的梯度更新方程为：
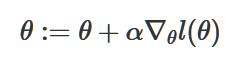
这个方程中我们使用了加号（线性回归中的梯度下降我们用的是负号），因为我们想要求的是函数的最大值。（这也是它被称为梯度上升的原因）。
假设训练集中只有一个训练样本(x,y)，我们对l(θ)求导以此来获得随机梯度上升的规则：
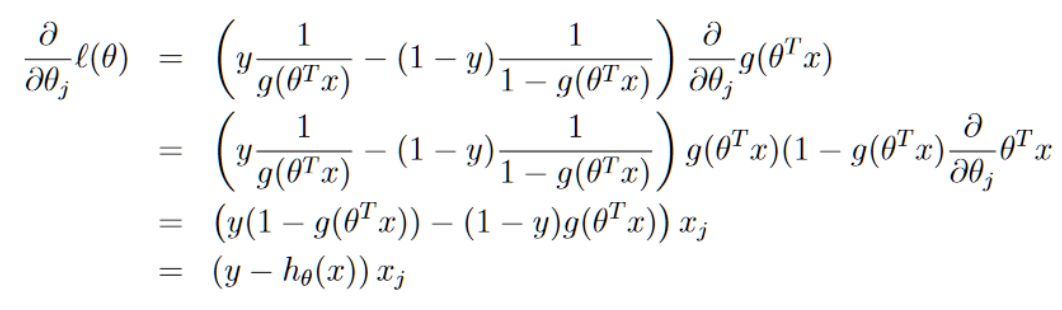
然后，我们将得出的结果应用到随机梯度上升的θ更新公式：
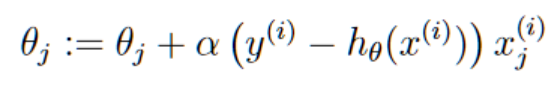
若是应用到批梯度上升则是：
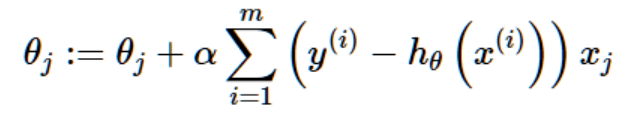
将他们和之前的最小均方法里面的梯度下降的θ的更新公式作比较，会发现二者一模一样。但是，事实上这里的hθ(x)已经变为关于θTx(i)的非线性函数（它的函数式和线性回归地h(x)是不一样的），所以这与我们的线性回归并不是同一个算法。
如果你还关注过其它的一些关于机器学习的消息的话，你会觉得这个函数很眼熟，因为这个函数，事实上也是神经网络中单个神经元常用的激励函数。
交流群
欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~