【SU Ruby教程】几何与变换(3):变换与变换矩阵

这一篇继续介绍 Geom 模块的另一个重要概念——变换类。和前两个部分的概念相同,变换类也有两种具体的类定义,分别是 Geom:: Transformation 和 Geom:: Transformation2d。其中前者用于 SketchUp 中三维空间的变换;后者用于 Layout,则不在教程内容范围内。
Geom:: Transformation 类是移动图元的操作工具,也是组件实例定位的必要组成。
几何与变换(3):变换与变换矩阵
| 【本期目录】 | |
(1)五种基本变换 ①单位变换 ②平移变换 ③旋转变换 ④缩放变换 ⑤坐标轴变换 | (3)变换组合 ①矩阵乘法 ②逆矩阵 ③矩阵插值 |
(2)应用变换 ①原点与坐标轴变换 ②点与向量的变换 ③图元的变换 | (4)变换矩阵详解 ①变换对象的矩阵表示 ②齐次坐标变换矩阵 |
(1)四种基本变换
①单位变换
直接通过 .new 方法无参数创建的变换类实例就是一个单位变换,单位变换表示一个完全没有变换的变换,相当于乘法中的1。使用 .identity? 方法可以判断一个 Geom:: Transformation 类实例是否是单位变换。
t = Geom::Transformation.newt.identity?#>> true
②平移变换
像某个方向移动一段距离的变换为平移变换,可以使用 .translation 方法创建这类变换类实例。
t1 = Geom::Transformation.translation([0,1,2])t2 = Geom::Transformation.translation(Geom::Point3d.new([0,1,2]))t3 = Geom::Transformation.translation(Geom::Vector3d.new([0,1,2]))
以上三种方法均可以创建平移变换实例,点坐标参数表示将原点移动到该点,而向量参数的含义亦是如此。另外,也可以将 .translation 改为 .new 方法,以上三种参数形式同样可以创建平移变换的实例。不过由于默认的创建对象方法参数形式繁多,分别可以创建不同类型的变换对象。因此为了避免不必要的混淆,推荐使用 .translation 来创建平移变换对象。
③旋转变换
绕一条直线旋转一定角度的变换为旋转变换,可以使用 .rotation 方法创建。
t1 = Geom::Transformation.rotation([0,0,0],[0,0,1],90.degrees)center = Geom::Point3d.new([0,0,0])normal = Geom::Vector3d.new([0,0,1])t2 = Geom::Transformation.rotation(center,normal,90.degrees)
以上两种方法都能够创建一个绕z轴正半轴90°旋转的变换对象, [center, normal] 即该变换的旋转轴。这里的角度是根据第二个参数向量的方向确定的,可以用右手定则记忆(下图)。
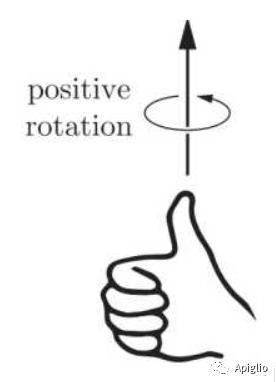
同样地,保持参数类型不变,将 .rotation 换成 .new 也同样可以创建旋转变换对象,但是出于相同的理由并不推荐。
④缩放变换
以原点为缩放中心,在x轴、y轴和z轴上分别缩放若干倍数的变换为缩放变换,可以使用 .scaling 方法创建。
t1 = Geom::Transformation.scaling(3)t2 = Geom::Transformation.scaling(2,3,4)pt = Geom::Point3d.new([100,100,-100])t3 = Geom::Transformation.scaling(pt,3)t4 = Geom::Transformation.scaling(pt,2,3,4)
缩放变换有四种创建方式,其中: t1 表示以原点为缩放中心放大3倍的变换; t2 表示以原点为缩放中心,在x轴、y轴、z轴上分别放大2、3、4倍的变换; t3 表示以 (100, 100, -100) 为缩放中心放大3倍的变换; t2 表示以 (100, 100, -100) 为缩放中心,在x轴、y轴、z轴上分别放大2、3、4倍。
同样地,保持参数类型不变,将 .scaling 换成 .new 也同样可以创建旋转变换对象,也不推荐这样使用。
⑤坐标轴变换
有时需要这样一种变换,将诸如 (x, z, -y) 这样的坐标转换成 (x, y, z) 坐标,这时就需要使用到坐标轴变换。
t1 = Geom::Transformation.axes([0,0,0],[1,0,0],[0,0,1],[0,-1,0])t2 = Geom::Transformation.axes(ORIGIN, X_AXIS, Z_AXIS, Y_AXIS.reverse)
其中, t2 是官方文档中的例子,使用到了 ORIGIN、 X_AXIS、 Y_AXIS 和 Z_AXIS 这些常量来表示特定的空间概念:

(2)应用变换
①原点与坐标轴的变换
一个 Geom:: Transformation 类实例预设有一些能够返回变换基本特征的方法,其中包括原点和坐标轴方向在这个变换后的空间位置。此处使用平移变换和坐标轴变换作为例子:
tr1 = Geom::Transformation.translation([0,1,2])tr2 = Geom::Transformation.axes([0,0,0],[1,0,0],[0,0,1],[0,-1,0])tr1.origin#>> Geom::Point3d(0, 1, 2)tr1.xaxis#>> Geom::Vector3d(1, 0, 0)tr1.yaxis#>> Geom::Vector3d(0, 1, 0)tr1.zaxis#>> Geom::Vector3d(0, 0, 1)tr2.origin#>> Geom::Point3d(0, 0, 0)tr2.xaxis#>> Geom::Vector3d(1, 0, 0)tr2.yaxis#>> Geom::Vector3d(0, 0, 1)tr2.zaxis#>> Geom::Vector3d(0, -1, 0)
②点与向量的变换
Geom:: Point3d 和 Geom:: Vector3d 类实例都有 .transform 和 .transform! 两个方法,用于应用具体的变换。很显然,两者区别在于前者只返回新的、变换后的实例;而以感叹号结尾的后者同时修改此实例的值。
pt = Geom::Point3d.new(2,-4,9)pt.transform!(tr1)puts pt#>> Geom::Point3d(2, -3, 11)vr = Geom::Vector3d.new(193,61,205)vr.transform!(tr2)puts vr#>> Geom::Vector3d(193, -205, 61)
③图元的变换
变换类最直观的作用就是用于移动当前模型中的图元,而移动图元需要使用的是 Sketchup:: Entities 类的 .transform_entities 方法,这个方法可以一次性变换一系列图元。
ents = Sketchup.active_model.entitiestrans = Geom::Transformation.rotation([0,0,0],[0,0,1],30.degrees)#令当前模型至少有两个群组ents.transform_entities(trans, ents.to_a)groups = ents.grep(Sketchup::Group)ents.transform_entities(trans, groups)ents.transform_entities(trans, groups[0], groups[1])
以上例子中,第4行表示将整个模型中的所有图元进行绕z轴正半轴30°的旋转,第5行则表示只旋转模型中所有群组,而第6行表示只旋转模型中第一个和第二个群组。 .transform_entities 的第一个参数必须是 Geom:: Transformation 类实例,而之后可以有多个参数,每个参数都可以是图元类或者是图元类的数组。可以理解成如下的定义:
module Sketchupclass Entitiesdef transform_entities(trans,*arg)entities_list = arg.flatten#对entities_list进行trans变换endendend
(3)变换组合
①矩阵乘法
当图元进行依次多个变换时,可以使用如下的变换方式:
t1 = Geom::Transformation.scaling(2,3,4)t2 = Geom::Transformation.rotation([0,0,0],[0,0,1],45.degrees)ents = Sketchup.active_model.entitiesent = ents[0]ents.transform_entities(t1,ent)ents.transform_entities(t2,ent)
如果变换的数量继续增加,不仅代码量会提高,每执行一次 .transform_entities 方法后就需要进行一次的模型更新也会大大影响代码执行效率。好在多个变换对象依次组合可以得到一个新的组合变换,而只需要通过 .*() 方法就可以实现。以上例子可以直接写成这样:
ents.transform_entities(t1*t2,ent)②逆矩阵
如果依次应用两个变换对象后,图元最终回到了没有变换之前的状态,就说这两个变换对象是互为对方的逆变换,通过 .inverse 和 .invert! 方法实现。可以从方法名称得出,前者只是返回一个变换对象的逆变换,而后者是在返回的基础上同时将此对象改为这个逆变换。
t3 = Geom::Transformation.translation([20,10,-30])puts t3.origin#>> Geom::Point(20, 10, -30)t3.invert!puts t3.origin#>> Geom::Point(-20, -10, 30)
根据逆变换的定义可以得知以下代码返回结果一定为 true:
# tn 为任意一个 Geom::Transformation 实例(tn*tn.inverse).identity?#>> true
③矩阵插值
Geom:: Transformation类中包含了五个类方法: .axes、 .translation、 .rotation、 .scaling 和 .interpolate,另外还有 .new 这样的构造方法。它们都是直接在类名之后使用,而不需要在类的实例之后使用。这意味着这些方法与具体的类实例没有关系,其执行内容是普遍的,而非针对具体某一个实例。Transformation 类的这几个类方法都可以理解成特定限定的 .new 方法,用以创建特定的变换类实例。
其他方法在前文都已经进行了介绍,都是返回特定意义的特殊变换对象。而 .interpolate 方法与这些方法有一点显著差异,它根据两个变换对象返回它们的线性插值结果。
例如以下的例子:
ents=Sketchup.active_model.entitiest=Geom::Transformation.newt1=Geom::Transformation.rotation([0,0,0],[0,0,1],180.degrees)t2=Geom::Transformation.translation([0,0,100])ttmp=Geom::Transformation.interpolate(t,t1*t2,1.0/18)acc=0timer=UI.start_timer(0.1,true){ents.transform_entities(ttmp, ents.to_a)if acc>=18 then UI.stop_timer(timer) endacc+=1}
其中, t1 为一个绕z轴旋转变换, t2 为沿z轴平移上升变换, t1*t2 表示这两个变换的组合。 .interpolate 方法在单位矩阵 t 和 t1*t2 之间寻找两个变换的中间状态。例如,第三个参数为 1.0/18,这就意味着方法返回了一个变换对象给 ttmp,使得连续变换18次 ttmp 就可以达到 t1*t2 的效果。如果参数是 1.0/4,那就是连续变换4次。
第6-11行是一个“超纲”的内容,大意为:每个0.1秒给整个模型应用一个 ttmp 变换,循环18次。最终的效果如下:
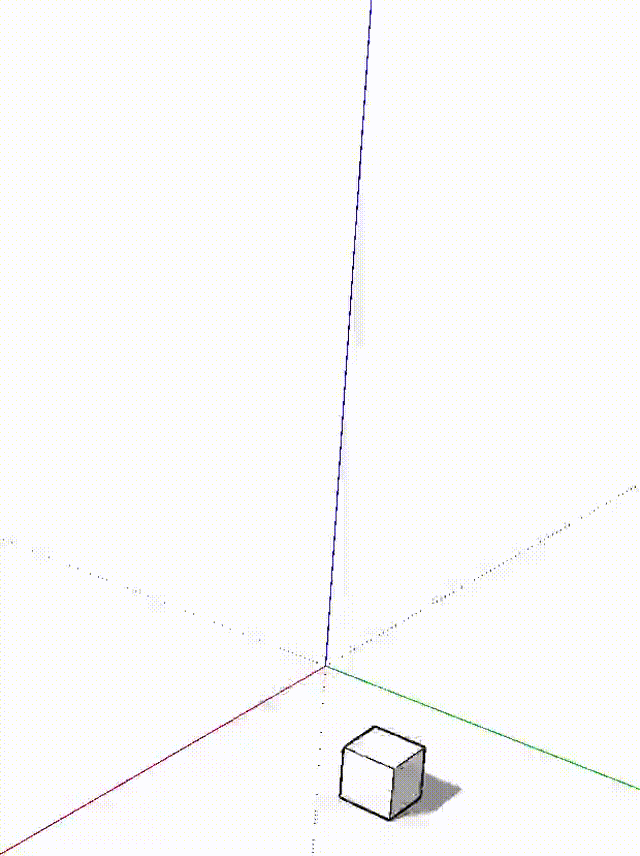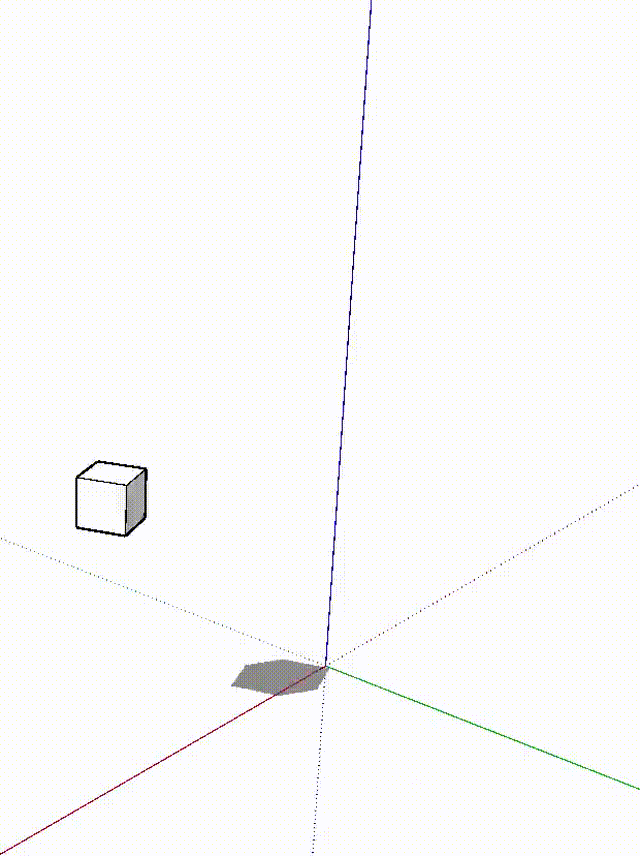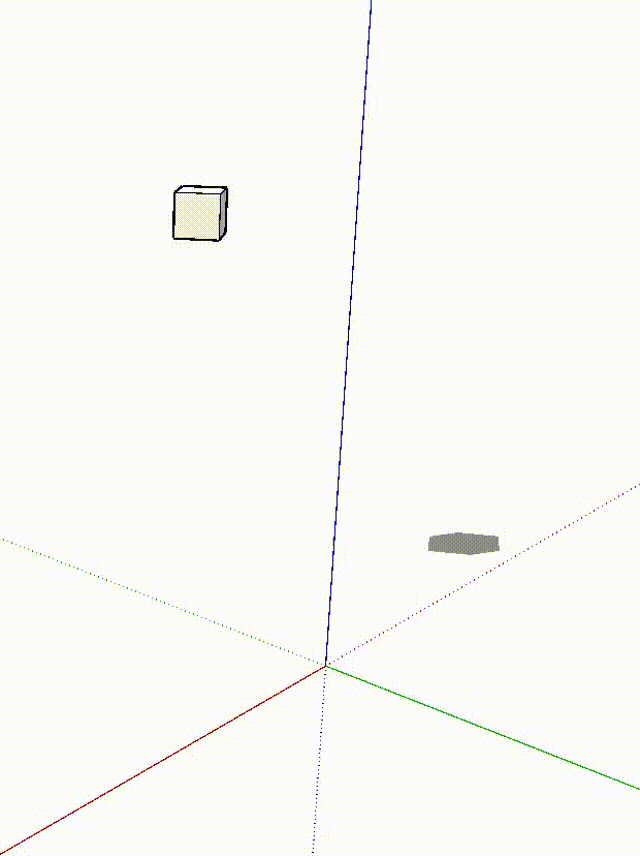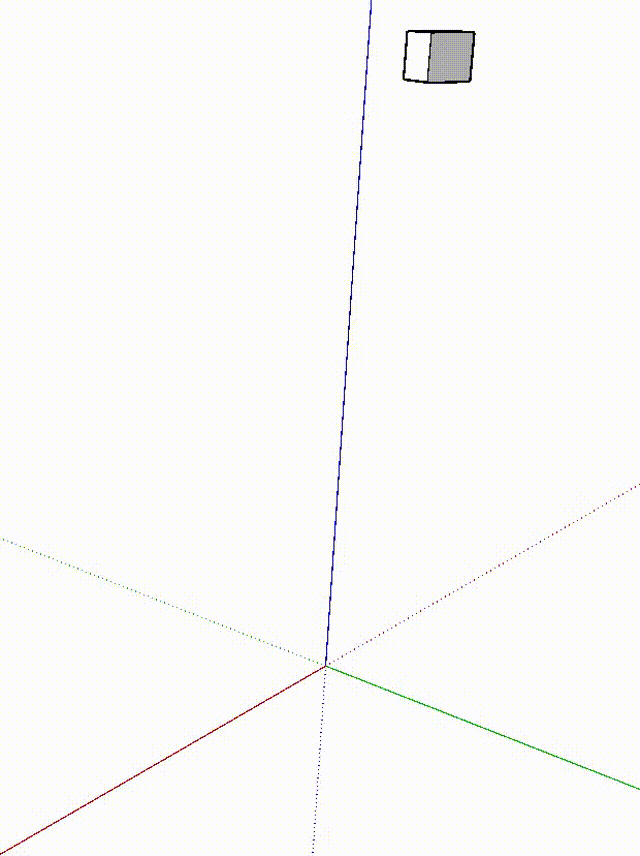
(4)变换矩阵详解
①变换对象的矩阵表示
变换对象所代表的空间变换可以用矩阵来表示,使用 .to_a 方法就可以得到这个矩阵。
t = Geom::Transformation.scaling(2,3,4)t.to_a#>> [2, 0, 0, 0, 0, 3, 0, 0, 0, 0, 4, 0, 0, 0, 0, 1]
相反,使用 .set! 方法可以通过这样形式的数组修改一个变换对象,或者直接使用 .new 方法。
mat=[2,0,0,0,0,3,0,0,0,0,4,0,0,0,0,1]t1 = Geom::Transformation.new(mat)t2 = Geom::Transformation.newt2.set!(mat)
只不过这里的“矩阵”是一个一维数组,并不符合对矩阵的直观感受。如果需要显示成矩阵的行列形式就需要额外的进行一些过程。
首先这个数组有16个元素,所以是一个4×4的矩阵,是三维空间的齐次坐标变换矩阵,一般情况下二维数组都是默认行排列,所以对于一个数组 t,其矩阵表示应该是这样的:
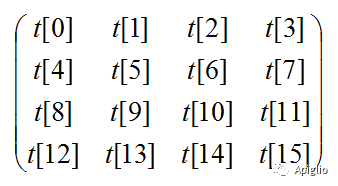
或者用数组的子界数组表示:
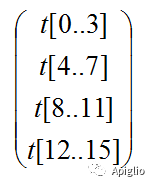
不过需要提前说明的是,这里使用行排列产生的矩阵结果适用于行向量的变换,而不是线性代数中更常使用的列向量。所以如果按照列向量变换的规则,变换矩阵应该写成以下形式:

若无特殊说明,本篇以下内容中出现的坐标均为行向量形式。
了解了这个规则以后,就可以自行在 Geom:: Transformation 类中追加显示矩阵的方法了:
module Geomclass Transformationdef matself.to_a.each_slice(4).to_a.unshift("").inject{|out,arr|"#{out}\r\n"+arr.unshift("").inject{|res,ele|"#{res}\t"+ele.round(3).to_s}}+"\r\n"enddef mattself.to_a.each_slice(4).to_a.transpose.unshift("").inject{|out,arr|"#{out}\r\n"+arr.unshift("").inject{|res,ele|"#{res}\t"+ele.round(3).to_s}}+"\r\n"endendend
其中定义了两个方法, mat 方法返回行向量变换的矩阵形式,而 matt 方法返回列向量变换的矩阵形式;之后的例子中都使用前者。
简单介绍一下实现方法: .each_slice(n) 方法可以将数组每n个一组作为新的数组返回给迭代器作为迭代变量。迭代器在之前的教程中有过一定的举例,这里使用了迭代器对象的 .to_a 方法将所有迭代值组成一个新的数组,以达到一维数组向二维数组的转换。在 matt 方法定义中的 .transpose 方法就是在这个二维数组的基础上进行的行列互换。至于 .round(n) 方法是可选项,可以将矩阵每个元素进行小数部分的长度限制。
关于其中的 .inject(res, item, &block) 方法,需要单独解释一下,这是一个带累计变量的迭代器。迭代器的两个参数 res 和 item 分别表示返回值和迭代变量,从数组的第1个元素开始迭代, res 的初始值为数组的第0个元素。常用于计算整个数组的特征值:
puts [1,2,3,4].inject{|res,item|res+=item}#>> 10 (返回各元素算数加和)puts [1,2,3,4].inject{|res,item|res=item if res<item}#>> 4 (返回数组中的最大值)#第二个例子如果用each来实现会变成这样:res=-Float::INFINITY #先给res一个最小值,使之小于数组中的任何一个元素[1,2,3,4].each{|item|res=item if res<item}puts res#此时res依然可以访问;#如果是inject,res作用域仅在块中。
②齐次坐标变换矩阵
Sketchup中的三维空间坐标变换为仿射变换,即一个线性变换加上一个平移变换。而三阶矩阵只能表示三维空间的线性变换,不能表示平移,因此就需要使用齐次坐标变换来表示。
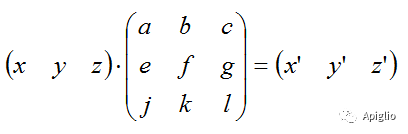
(3阶线性变换矩阵)
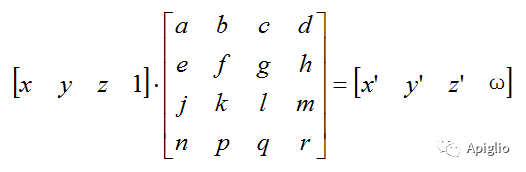
(3+1阶齐次坐标变换矩阵)
齐次方程通过引入哑元 ω 来表示原点的平移情况:当第四元 ω≠0 时坐标表示三维空间内一点;当第四元 ω=0 时坐标表示三维空间内一个向量。向量的坐标与前三元一致;当 ω=1 时,点坐标与前三元一致。齐次坐标所有元同时乘一个非零常数k后,表示的依然是同一个点。因此如果点的齐次坐标 ω≠1 时,可以通过四元同时除以ω得到标准化的齐次坐标:
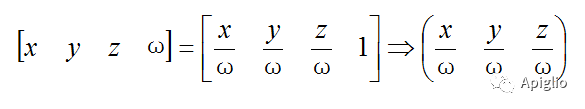
(齐次坐标与笛卡尔坐标的转换)
因此,对于变换矩阵 [a, b, c, d, e, f, g, h, j, k, l, m, n, p, q, r] 来说,点 (x, y, z) 变换后的坐标可以用以下方程表示:
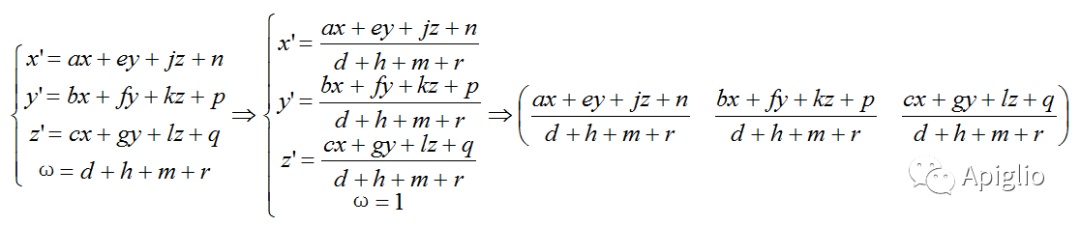
我们可以把这个矩阵拆成四个部分:
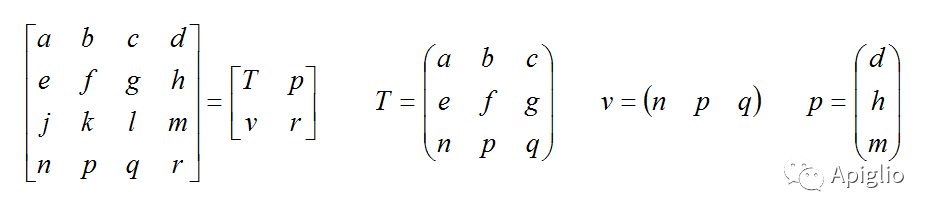
T 表示仿射变换中的线性变换,也就是以原点为中心的缩放、旋转、错切等变换。 v 表示仿射变换中平移的方向和距离。 p 与投影变换有关,其值的改变与 SketchUp 中的变换似乎并无关系[注]。r 则为整体的比例系数,相当于点的齐次坐标中的哑元ω。
具体来看一下几个基本变换的矩阵形式
(i)单位矩阵
t1=Geom::Transformation.newt1.mat#>> 1.0 0.0 0.0 0.0#>> 0.0 1.0 0.0 0.0#>> 0.0 0.0 1.0 0.0#>> 0.0 0.0 0.0 1.0
单位矩阵对角线全为1,其余全为0:

(ii)平移矩阵
t2=Geom::Transformation.translation([100,200,-300])t2.mat#>> 1.0 0.0 0.0 0.0#>> 0.0 1.0 0.0 0.0#>> 0.0 0.0 1.0 0.0#>> 100.0 200.0 -300.0 1.0
平移矩阵在单位矩阵基础上令 v 为平移向量坐标:
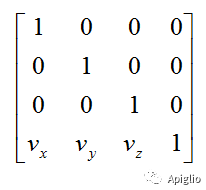
(iii)旋转矩阵
t3=Geom::Transformation.rotation([100,100,0],[0,0,1],90.degrees)t3.mat#>> 0.0 1.0 0.0 0.0#>> -1.0 0.0 0.0 0.0#>> 0.0 0.0 1.0 0.0#>> 200.0 0.0 0.0 1.0
旋转矩阵中, T 为三维旋转的线性变换矩阵, v 为旋转后的原点坐标(以下为绕z轴方向旋转的例子):
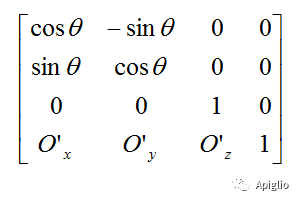
(iv)缩放矩阵
t4=Geom::Transformation.scaling([100,-100,0],2,2,2)t4.mat#>> 2.0 0.0 0.0 0.0#>> 0.0 2.0 0.0 0.0#>> 0.0 0.0 2.0 0.0#>> -100.0 100.0 0.0 1.0
缩放矩阵在对角线以外均为0。对于等比例缩放S倍的矩阵 M,有 diag(M) = (1, 1, 1, S);对于不等比例的缩放矩阵 N,则有 diag(N) = (Sx, Sy, Sz, 1)。当然,如果不是以原点为缩放中心, v 则是原点缩放后的坐标。
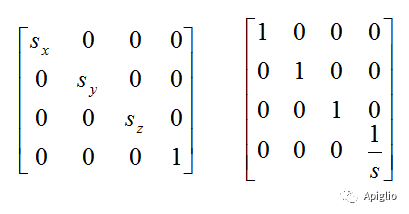
(v)组合变换
tt = t1*t4tt.mat#>> 2.0 0.0 0.0 0.0#>> 0.0 2.0 0.0 0.0#>> 0.0 0.0 2.0 0.0#>> -100.0 100.0 0.0 1.0
多个变换的依次组合在 Geom:: Transformation 类中使用的是 .*() 方法,对应矩阵的乘法,以下用二阶举个例子:
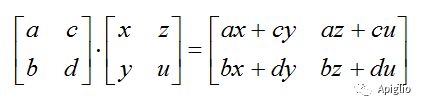
SketchUp提供的变换都是不改变图形形状的变换,其组合也都保持这一特点,但是可以自己通过齐次坐标变换矩阵的定义实现一些特殊的改变图元形状的变换,例如:错切变换和投影变换。
(vi)错切变换
mat_1 = [1,1,0,0,0,1,1,0,1,0,1,0,0,0,0,2]t5=Geom::Transformation.new(mat_1)#令当前模型有且只有一个正方体群组ents = Sketchup.active_model.entitiesents.transform_entities(t5,ents[0])
在三个轴方向上都进行了等比例的错切后:
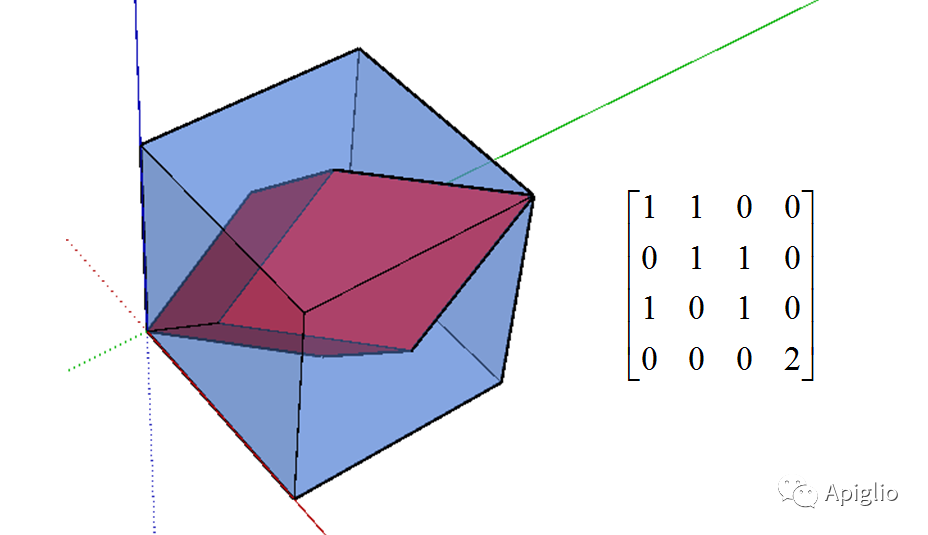
(错切变换)
(vii)投影变换
mat_2 = [1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,1]t6=Geom::Transformation.new(mat_2)t7=Geom::Transformation.rotation([0,0,0],[0,1,0],45.degrees)t8=t7*t6*t7.inverse#令当前模型有且只有一个正方体群组ents = Sketchup.active_model.entitiesents.transform_entities(t8,ents[0])
使用“旋转-投影-恢复旋转”的方式组合一个新的变换,并将正方体投影在平面 x+z=0 上:
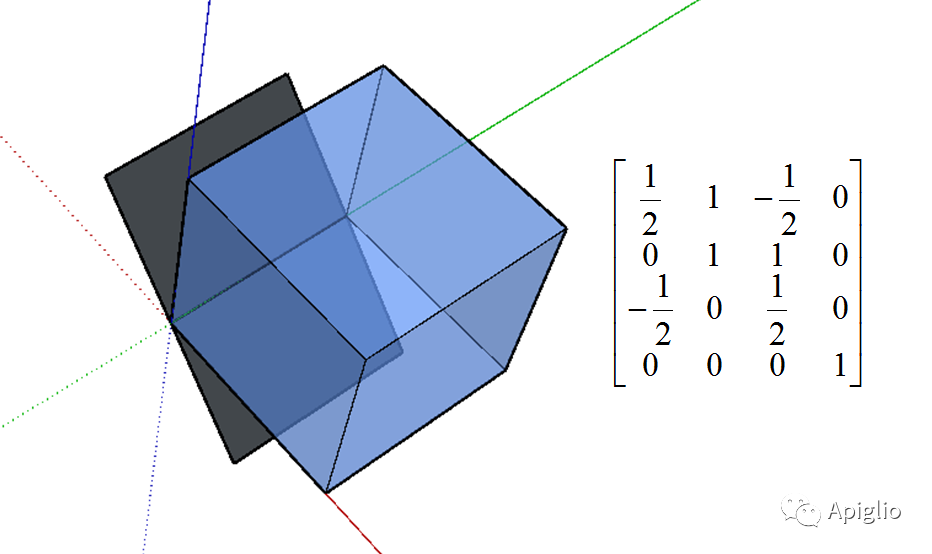
(投影变换)
不过需要额外说明:投影变换只是作为自定义变换的例子存在,并不是那么有应用意义,它会导致大量重合图元,应当采用更好的方法来生成新的图元。而根据特定条件生成特定图元则需要在之后的教程中涉及。
以上就是本篇教程的全部内容,篇末为文中一处的注释内容和补充内容。
注:关于 Geom:: Transformation 类对象对应的的矩阵,相关资料描述较少。再加上本人也是第一次接触齐次坐标系,找不到很好的切入点深究这个问题。初步的测试结果是向量 p 的值变化不会对一个具体变换产生影响,因此只能暂时粗略地得出“似乎并无关系”。
另外,矩阵插值中介绍的 .interpolate 方法作为类方法,进行两个矩阵的线性插值。而在向量的计算中也有一个类似的方法,即 .linear_combination 方法,它也根据两个空间概念和一个0~1的位置数值进行线性插值。不过在向量的教程中并没有专门提及,因为这个方法可以很轻松的实现。
本文编号:SU-R08
