细讲傅立叶变换
日期:2020年08月31日
正文共:1679字12图
预计阅读时间:5分钟
作者:赵一帆

当你给它一个信号(或函数),傅里叶变换能采用基于时间的模式,测量该信号(或函数)的每一个可能周期,告诉你组成该信号(或函数)的循环周期的振幅、偏移量和旋转速度等“原料”。
第一个,网孔最大的过滤网把蛋过滤了出来 第二个,网孔适中的过滤网把饭过滤了出来 第三个,网孔较小的过滤网把盐巴过滤了出来 ……………… 通过无数孔径不一的过滤网,不同“原料”被过滤出来,而这些过滤网统称为“过滤器(filter)”。
【题外话】:笔者最喜欢的两个数学家分别是“泰勒”和“傅里叶”,他们的两个定理貌似揭示了世界的真理。 泰勒说:“任何函数都可以转换成无穷多个幂函数的和。”
“泰勒的这句话,给后来计算机的发展带来了巨大贡献,举个例子,计算机并没办法计算类似于sin、cos这样的函数,只能通过将他们转换为各个幂函数的和来实现。”
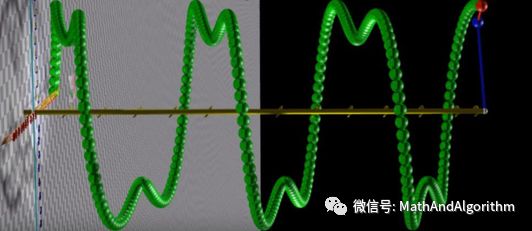
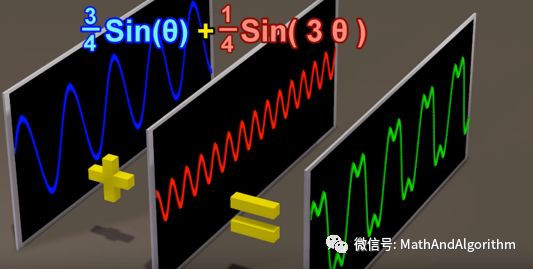
傅里叶说:“任何信号(或函数)都可以转换成无穷多个周期函数的和。”这句话的涵义,我们后面会慢慢细讲。
如果地震波可被分解,找出不同的振幅和速度,那么我们可以针对地震的特定振幅和速度设计对应的抗震建筑物。 如果声波可被分解成低音和高音,我们就可以放大我们关心的部分,缩小我们不关心的部分。 "比如你喜欢小提琴,那便可以提高高音部分,隐去低音部分。 如果你喜欢低音贝斯,那么你就可以提高低音部分,隐去高音部分。" 如果计算机数据可以用震荡波形表示,且其中包含可忽略的数据,那么就可以用傅里叶变换滤去不重要的数据。这在数据科学中被叫为“数据滤波器”。 如果是收音机的无线电波,那么我们就可以收听到特定频率的广播。 傅里叶变换在工程中的应用是十分广泛的,以上举例的只是小小一部分,希望能助于你们理解傅里叶变换背后的根源。
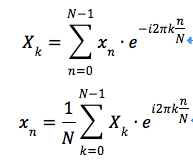
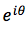 相当于单位向量绕着原点旋转
相当于单位向量绕着原点旋转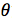 角
角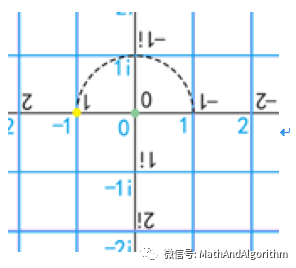
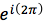 就是单位向量绕着原点旋转一周
就是单位向量绕着原点旋转一周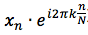 就是长度为
就是长度为 的向量绕着原点旋转
的向量绕着原点旋转 (或原函数)
(或原函数)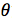 轴。
轴。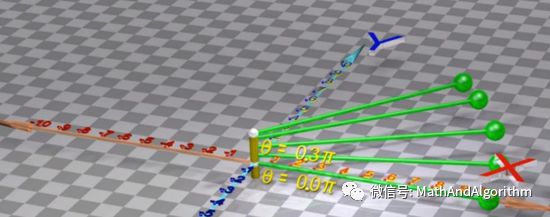

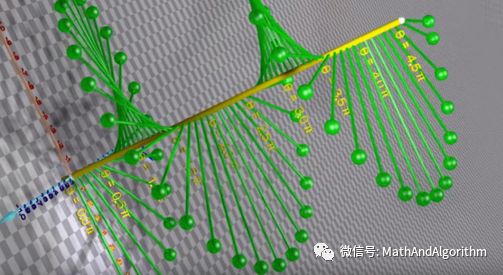
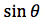 函数
函数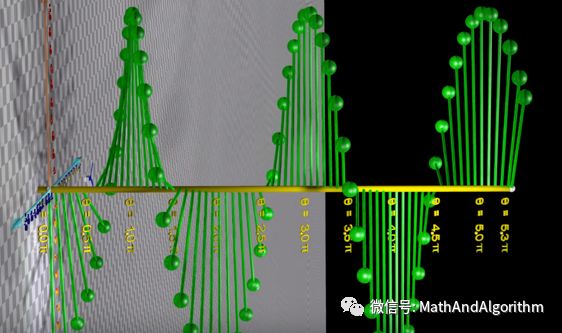

— THE END —

评论