一作的亲自解读!CVPR 2022最佳学生论文奖研究了什么?
来源:机器之心
距离 CVPR 2022 各大奖项公布没多久,来自同济大学研究生、阿里达摩院研究型实习生陈涵晟为我们解读最佳学生论文奖。

论文链接:https://arxiv.org/abs/2203.13254 代码链接:https://github.com/tjiiv-cprg/EPro-PnP
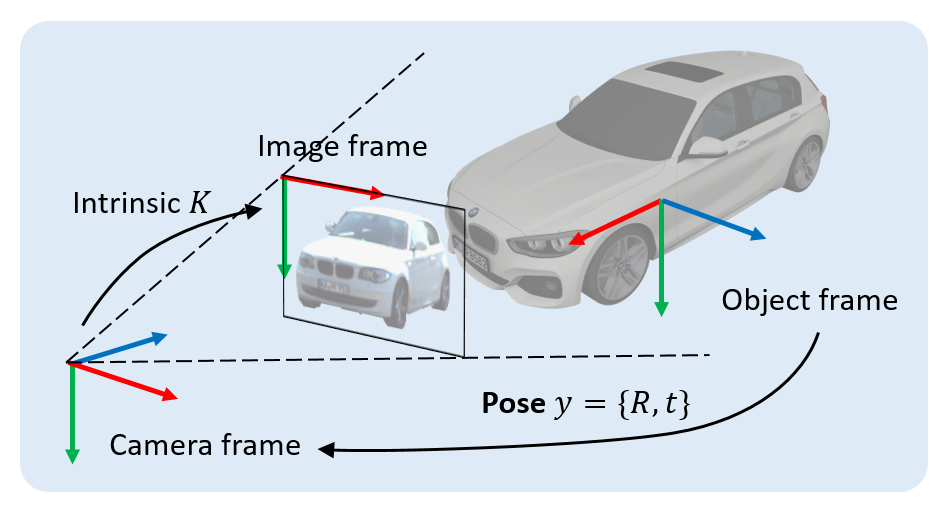
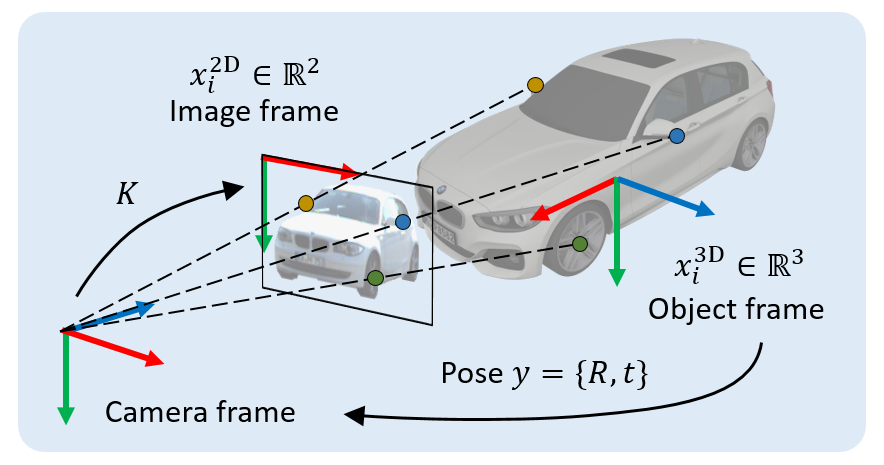
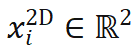 ),同时在物体坐标系中找出与之相关联的 N 个 3D 点(第 i 点 3D 坐标记作
),同时在物体坐标系中找出与之相关联的 N 个 3D 点(第 i 点 3D 坐标记作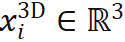 ),有时还需要获取各对点的关联权重(第 i 对点的关联权重记作
),有时还需要获取各对点的关联权重(第 i 对点的关联权重记作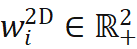 )。根据透视投影约束,这 N 对 2D-3D 加权关联点隐式地定义了物体的最优位姿。具体而言,我们可以找出使重投影误差最小的物体位姿
)。根据透视投影约束,这 N 对 2D-3D 加权关联点隐式地定义了物体的最优位姿。具体而言,我们可以找出使重投影误差最小的物体位姿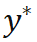 :
: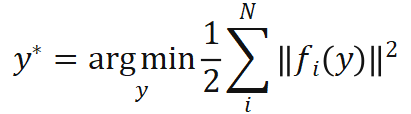
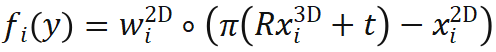 ,表示加权重投影误差,是位姿的
,表示加权重投影误差,是位姿的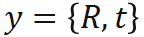 函数。
函数。 表示含有内参的相机投影函数,
表示含有内参的相机投影函数,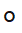 表示元素乘积。PnP 方法常见于物体几何形状已知的 6 自由度位姿估计任务中。
表示元素乘积。PnP 方法常见于物体几何形状已知的 6 自由度位姿估计任务中。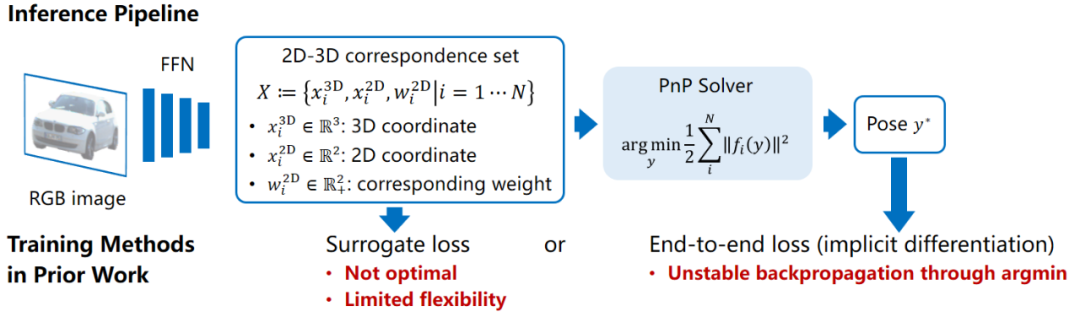
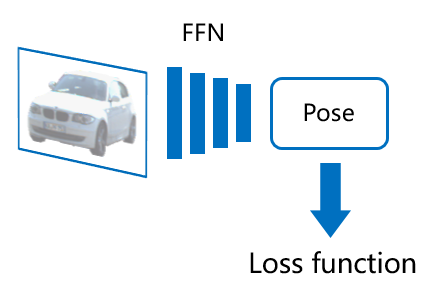
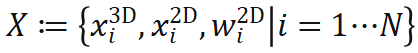 。相比于直接位姿预测,这一深度学习结合传统几何视觉算法的模型有非常好的可解释性,其泛化性能较为稳定,但在以往的工作中模型的训练方法存在缺陷。很多方法通过构建代理损失函数,去监督 X 这一中间结果,这对于位姿而言不是最优的目标。例如,已知物体形状的前提下,可以预先选取出物体的 3D 关键点,然后训练网络去找出对应的 2D 投影点位置。这也意味着代理损失只能学习 X 中的部分变量,因此不够灵活。如果我们不知道训练集中物体的形状,需要从零开始学习 X 中的全部内容该怎么办?
。相比于直接位姿预测,这一深度学习结合传统几何视觉算法的模型有非常好的可解释性,其泛化性能较为稳定,但在以往的工作中模型的训练方法存在缺陷。很多方法通过构建代理损失函数,去监督 X 这一中间结果,这对于位姿而言不是最优的目标。例如,已知物体形状的前提下,可以预先选取出物体的 3D 关键点,然后训练网络去找出对应的 2D 投影点位置。这也意味着代理损失只能学习 X 中的部分变量,因此不够灵活。如果我们不知道训练集中物体的形状,需要从零开始学习 X 中的全部内容该怎么办?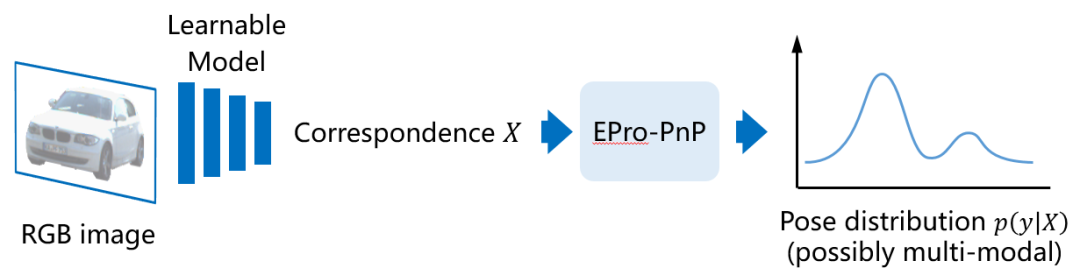
 对于 X 是可导的。首先基于重投影误差定义位姿的似然函数:
对于 X 是可导的。首先基于重投影误差定义位姿的似然函数: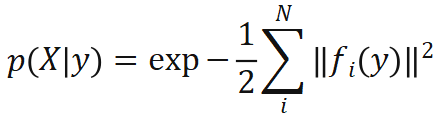
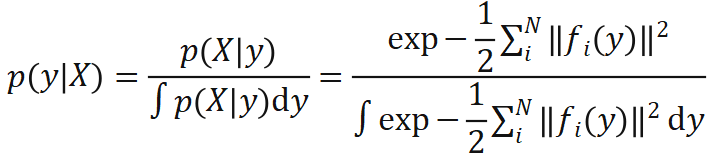
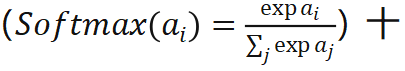 分接近,其实 EPro-PnP 的本质就是将softmax从离散阈搬到了连续阈,把求和
分接近,其实 EPro-PnP 的本质就是将softmax从离散阈搬到了连续阈,把求和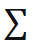 换成了积分
换成了积分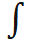 。
。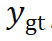 ,则可以定义目标位姿分布
,则可以定义目标位姿分布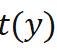 。此时可以计算 KL 散度
。此时可以计算 KL 散度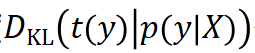 作为训练网络所用的损失函数(因
作为训练网络所用的损失函数(因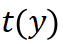 固定,也可以理解为交叉熵损失函数)。在目标
固定,也可以理解为交叉熵损失函数)。在目标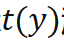 趋近于 Dirac 函数的情况下,基于 KL 散度的损失函数可以简化为以下形式:
趋近于 Dirac 函数的情况下,基于 KL 散度的损失函数可以简化为以下形式: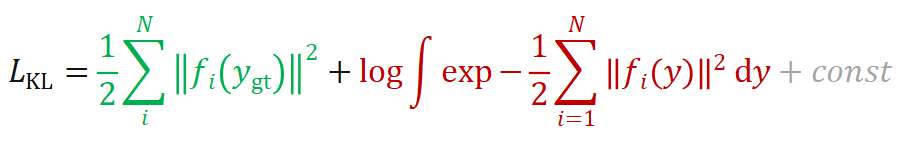
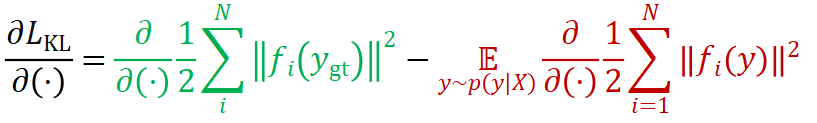
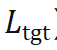 )试图降低位姿真值
)试图降低位姿真值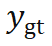 的重投影误差,第二项(记作
的重投影误差,第二项(记作 )试图增大预测位姿
)试图增大预测位姿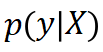 各处的重投影误差。二者方向相反,效果如下图(左)所示。作为类比,右边就是我们在训练分类网络时常用的分类交叉熵损失。
各处的重投影误差。二者方向相反,效果如下图(左)所示。作为类比,右边就是我们在训练分类网络时常用的分类交叉熵损失。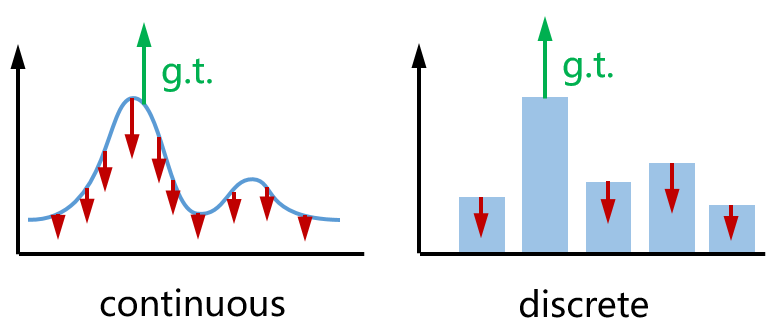
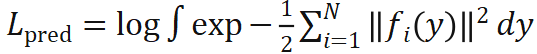 中含有积分,这一积分没有解析解,因此必须通过数值方法进行近似。综合考虑通用性,精确度和计算效率,我们采用蒙特卡洛方法,通过采样来模拟位姿分布。
中含有积分,这一积分没有解析解,因此必须通过数值方法进行近似。综合考虑通用性,精确度和计算效率,我们采用蒙特卡洛方法,通过采样来模拟位姿分布。
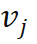 的位姿样本
的位姿样本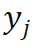 ,我们将这一过程称作蒙特卡洛 PnP:
,我们将这一过程称作蒙特卡洛 PnP: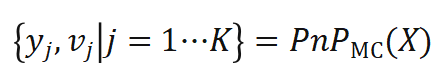
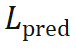 可以近似为关于权重
可以近似为关于权重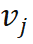 的函数,且
的函数,且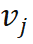 可以反向传播:
可以反向传播: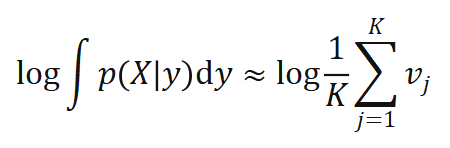
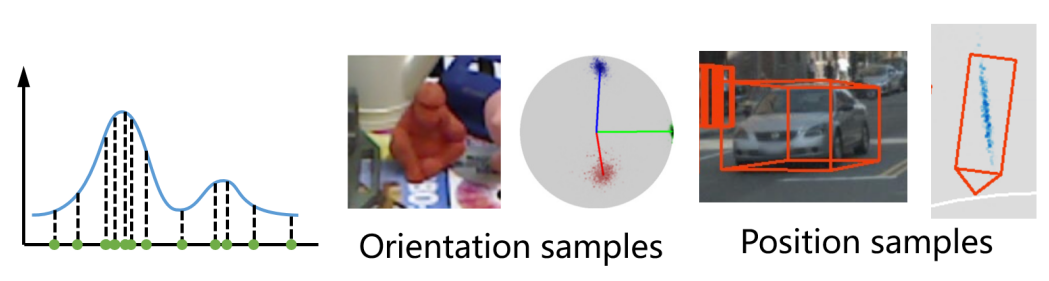
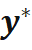 。常用的高斯 - 牛顿及其衍生算法通过迭代优化求解
。常用的高斯 - 牛顿及其衍生算法通过迭代优化求解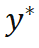 ,其迭代增量是由代价函数
,其迭代增量是由代价函数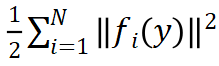 的一阶和二阶导数决定的。为使 PnP 的解
的一阶和二阶导数决定的。为使 PnP 的解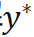 更接近真值
更接近真值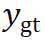 ,可以对代价函数的导数进行正则化。设计正则化损失函数如下:
,可以对代价函数的导数进行正则化。设计正则化损失函数如下: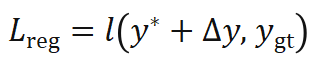
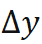 为高斯 - 牛顿迭代增量,与代价函数的一阶和二阶导数有关,且可以反向传播,
为高斯 - 牛顿迭代增量,与代价函数的一阶和二阶导数有关,且可以反向传播,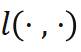 表示距离度量,对于位置使用 smooth L1,对于朝向使用 cosine similarity。在
表示距离度量,对于位置使用 smooth L1,对于朝向使用 cosine similarity。在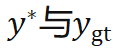 不一致时,该损失函数促使迭代增量
不一致时,该损失函数促使迭代增量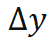 指向实际真值。
指向实际真值。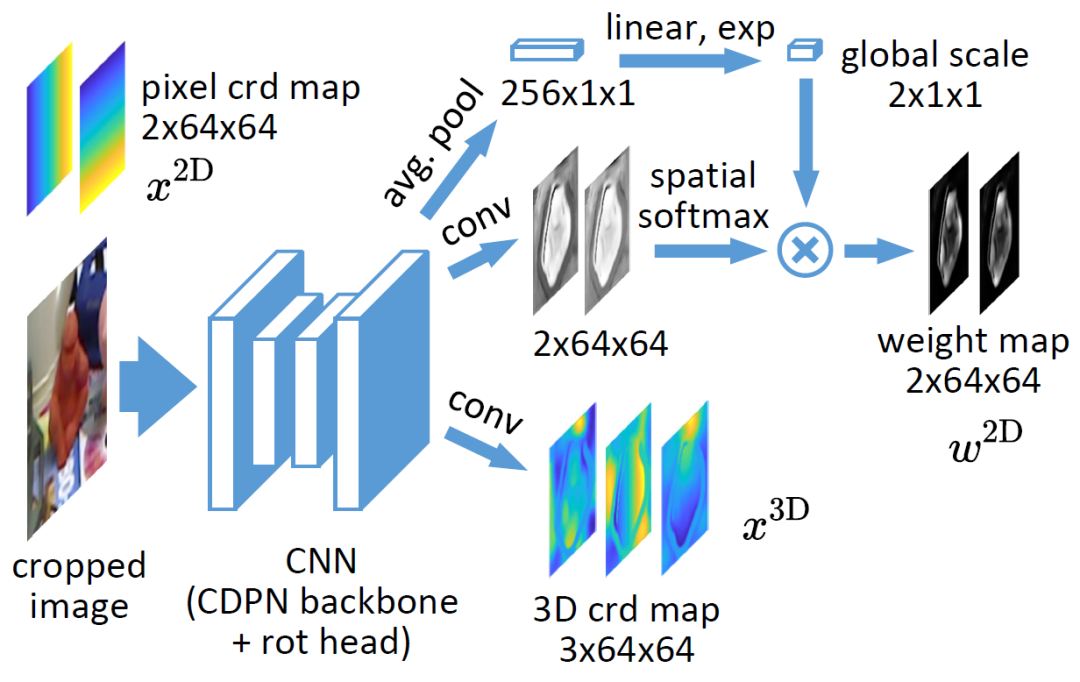
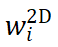 进行归一化,使其具有类似 attention map 的性质,可以关注相对重要的区域,实验证明权重归一化也是稳定收敛的关键。Global weight scaling 反映了位姿分布
进行归一化,使其具有类似 attention map 的性质,可以关注相对重要的区域,实验证明权重归一化也是稳定收敛的关键。Global weight scaling 反映了位姿分布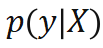 的集中程度。该网络仅需 EPro-PnP 的蒙特卡洛位姿损失就可以训练,此外可以增加导数正则化,以及在物体形状已知的情况下增加额外的 3D 坐标回归损失。
的集中程度。该网络仅需 EPro-PnP 的蒙特卡洛位姿损失就可以训练,此外可以增加导数正则化,以及在物体形状已知的情况下增加额外的 3D 坐标回归损失。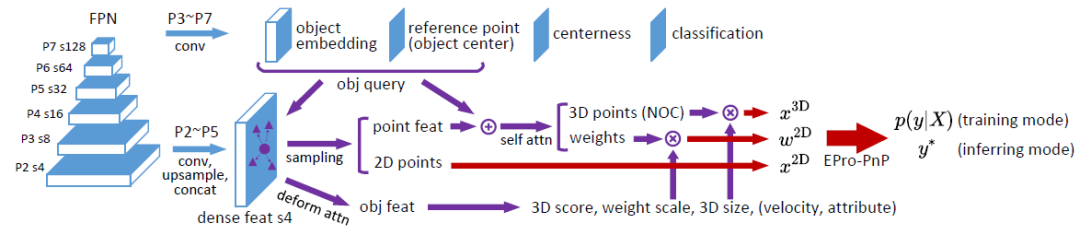
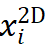 )。采样后的 feature 经由 attention 操作聚合为 object feature,用于预测物体级别的结果(3D score,weight scale,3D box size 等)。此外,采样后各点的 feature 在加入 object embedding 并经由 self attention 处理后输出各点所对应的的 3D 坐标
)。采样后的 feature 经由 attention 操作聚合为 object feature,用于预测物体级别的结果(3D score,weight scale,3D box size 等)。此外,采样后各点的 feature 在加入 object embedding 并经由 self attention 处理后输出各点所对应的的 3D 坐标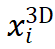 和关联权重
和关联权重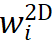 。所预测的
。所预测的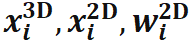 全部可由 EPro-PnP 的蒙特卡洛位姿损失训练得到,不需要额外正则化就可以收敛并有较高的精度。在此基础上,可以增加导数正则化损失和辅助损失进一步提升精度。
全部可由 EPro-PnP 的蒙特卡洛位姿损失训练得到,不需要额外正则化就可以收敛并有较高的精度。在此基础上,可以增加导数正则化损失和辅助损失进一步提升精度。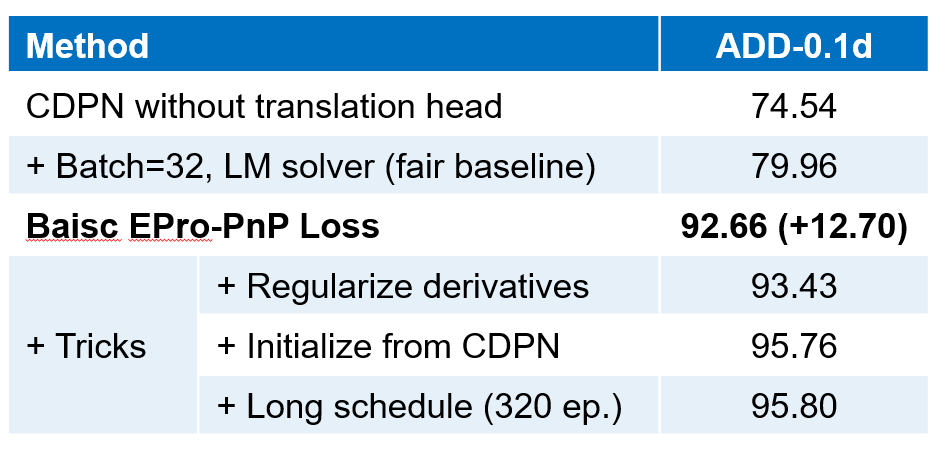
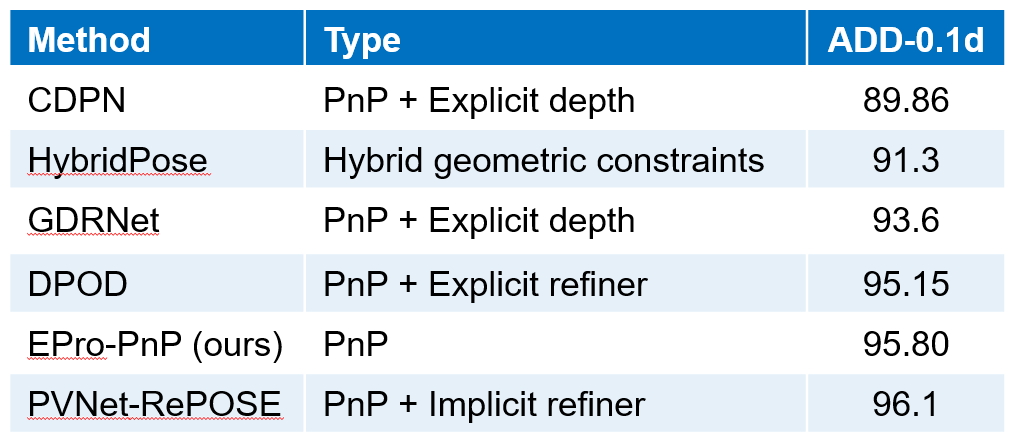
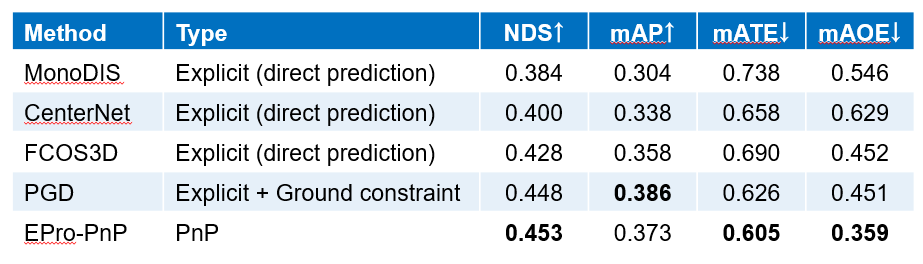
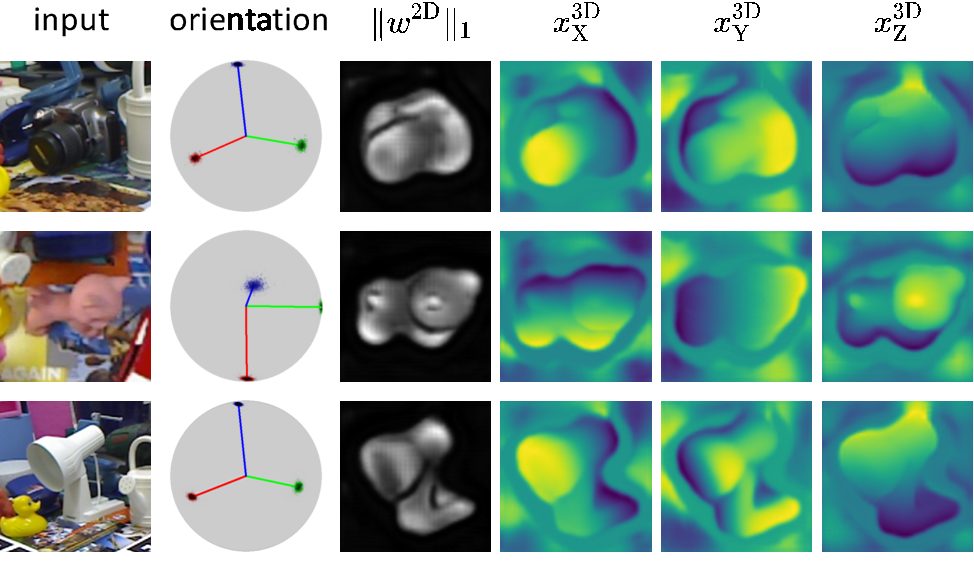
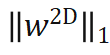 对图像中的重要区域进行了高光,类似于 attention 机制。由损失函数分析可知,高光区域对应的是重投影不确定性较低以及对位姿变动较为敏感的区域。
对图像中的重要区域进行了高光,类似于 attention 机制。由损失函数分析可知,高光区域对应的是重投影不确定性较低以及对位姿变动较为敏感的区域。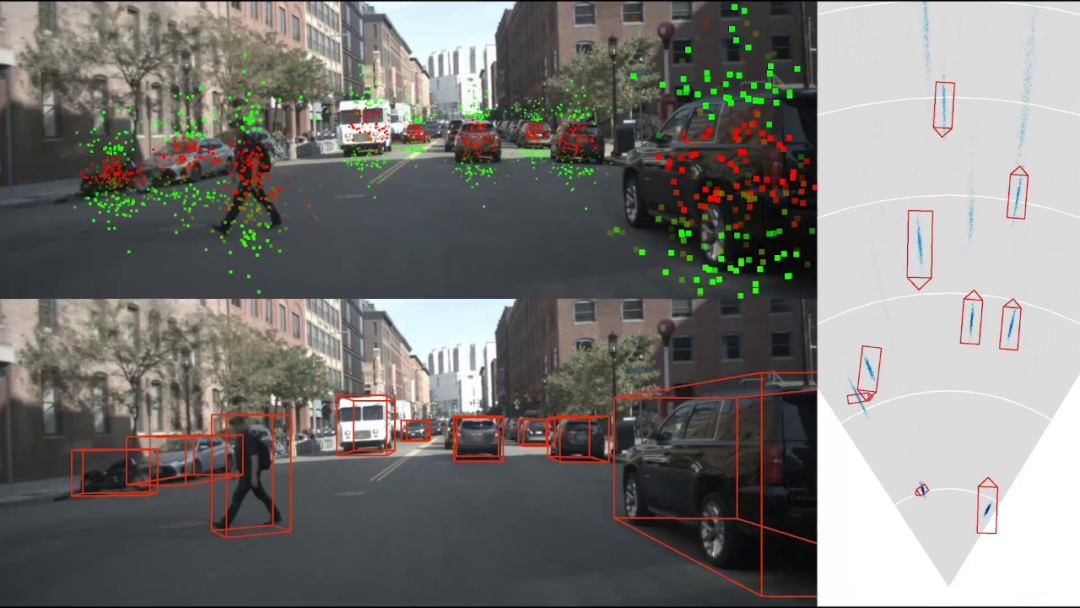
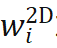 水平 X 分量较高的带你,绿色表示
水平 X 分量较高的带你,绿色表示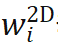 垂直 Y 分量较高的点。绿色点一般位于物体上下两端,其主要作用是通过物体高度来推算物体的距离,这一特性并非人为指定,完全是自由训练的结果。右图显示了俯视图上的检测结果,其中蓝色云图表示物体中心点位置的分布密度,反映了物体定位的不确定性。一般远处的物体定位不确定性大于近处的物体。
垂直 Y 分量较高的点。绿色点一般位于物体上下两端,其主要作用是通过物体高度来推算物体的距离,这一特性并非人为指定,完全是自由训练的结果。右图显示了俯视图上的检测结果,其中蓝色云图表示物体中心点位置的分布密度,反映了物体定位的不确定性。一般远处的物体定位不确定性大于近处的物体。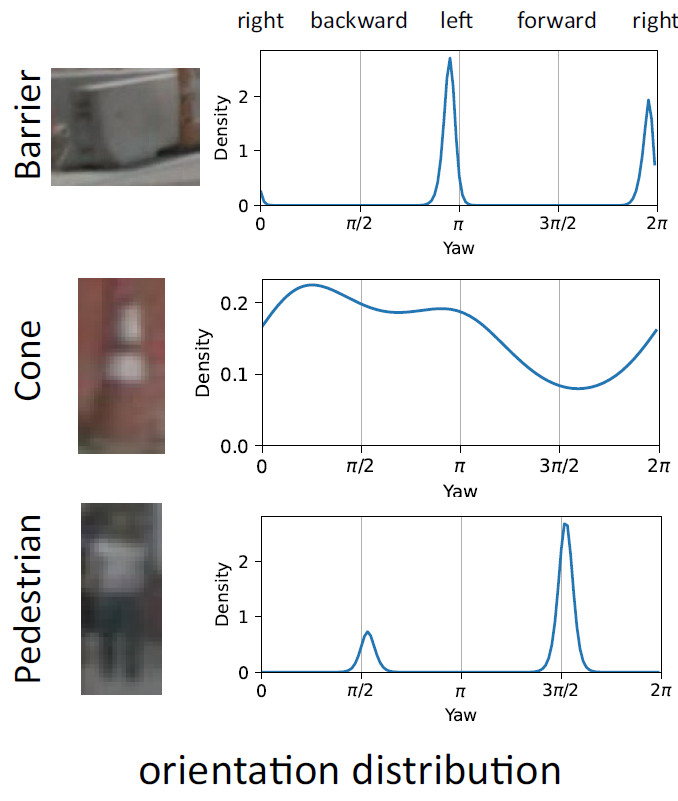
评论
