【SU Ruby教程】几何与变换(2):范围

上一篇用较长的篇幅介绍了向量与点线面的表示方法,而这一篇继续关注Geom模块中提供的另一个空间概念——范围。
范围(Bounds),是一组空间坐标在各坐标轴方向上最大最小值的范围,对于SketchUp中的三维空间而言,是一个其各条棱与坐标轴平行的、包含一组坐标的最小长方体。
Geom模块中有三个与“Bounds”有关的类定义,分别是 Geom:: Bounds2d、Geom:: OrientedBounds2d 和 Geom:: BoundingBox。其中前两个是二维的范围,与 Geom:: Point2d、 Geom:: Vector2d 均是二维空间概念,主要用于 Layout, SketchUp 则一般不会使用到。
因此本篇重点在于介绍Geom:: BoundingBox类。
几何与变换(2):范围
| 【本期目录】 | |
(1)范围类 ①Geom::BoundingBox类 ②三种访问方法 | (3)判断与运算 ①判断是否在范围内 ②并集运算 ③交集运算 |
(3)范围基本属性 ①锚点与中点 ②长宽高与对角线 | |
(1)范围类
①Geom:: BoundingBox类
Geom 模块定义了 BoundingBox 类用于表示空间范围,用于判断空间中某点是否在某个范围中。
SU中的图元实体包含多个空间点,而通过这些点可以得到一个空间范围,这个范围在一定程度上能够反映图元的空间位置。通过比较两个图元的范围可以粗略地判断两个图元是否有可能相交。
②三种访问方法
一般情况下,我们不需要自己新建 Geom:: BoundingBox 类的实例,而是直接通过 Sketchup:: Drawingelement 类实例的 .bounds 方法返回范围类的一个实例:
#令当前模型至少有一个图元puts Sketchup.active_model.entities[0].bounds#>> #<Geom::BoundingBox:0x0000000051afe0>
与Sketchup:: Vertex的 .position 方法一样, .bounds 方法也是根据图元的空间位置范围创建一个新的 BoundingBox 类实例,所以对同一个图元多次调用 .bounds 方法会返回不同的范围类实例,尽管这些实例所代表的范围是一致的。
除了图元类,Sketchup:: Model类也可以返回整个模型所有图元的空间范围,同样是 .bounds 方法:
puts Sketchup.active_model.bounds#>> #<Geom::BoundingBox:0x0000000b5bb638>
依附于模型的范围类固然十分便捷,但有时可能需要使用抽象的、不依附于模型的范围类,这时就需要使用 .new 方法这种最基本的创建方式了。
puts Geom::BoundingBox.new#>> #<Geom::BoundingBox:0x0000000b5694c8>
不同于前两个方法获得的 BoundingBox 实例,此时新建的实例是一个空范围,可以用 .empty? 方法和 .valid? 方法检验。
#令当前模型至少有一个图元bb_1 = Sketchup.active_model.boundsbb_2 = Geom::BoundingBox.newputs bb_1.empty? #>> falseputs bb_1.valid? #>> trueputs bb_2.empty? #>> trueputs bb_2.valid? #>> false
以上两个方法结果总是相反的,因此 !bb. empty? 和 bb. valid? 相同, !bb. valid? 和 bb. empty? 相同。
如果当前模型中没有任何图元, Sketchup. active_model. bounds. empty? 的结果为 true。
(2)范围基本属性
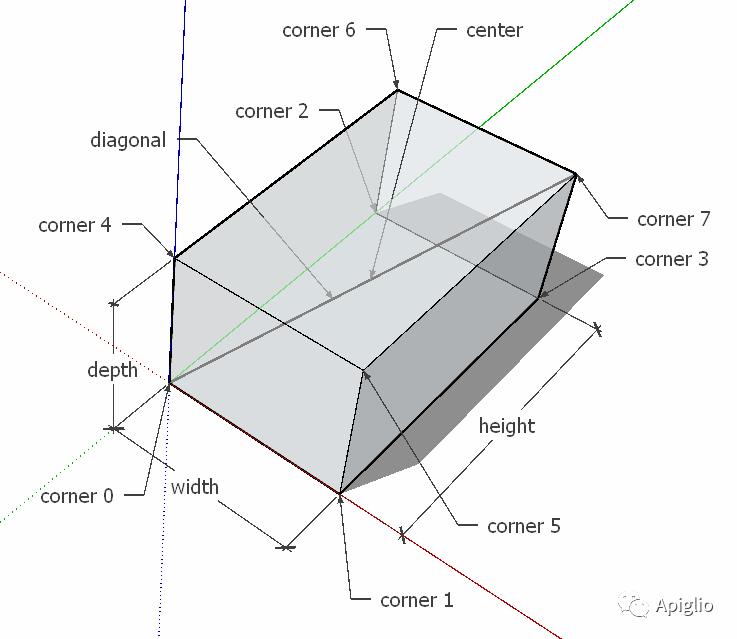
①锚点与中点
如上图,一个 BoundingBox 类实例包含九个关键点,八个顶点和一个中心点,它们分别由以下方法返回,返回类型为Geom:: Point3d:
bb = Sketchup.active_model.boundsputs bb.center#>> (1061443.319932mm, 1074824.726654mm, 1088928.066406mm)corners=[]for point_id in 0..7 docorners << bb.corner(point_id)endputs corners#>> [Point3d(-17306.2, -30879.8, -8293.75),#>> Point3d(100884, -30879.8, -8293.75),#>> Point3d(-17306.2, 115512, -8293.75),#>> Point3d(100884, 115512, -8293.75),#>> Point3d(-17306.2, -30879.8, 94036.1),#>> Point3d(100884, -30879.8, 94036.1),#>> Point3d(-17306.2, 115512, 94036.1),#>> Point3d(100884, 115512, 94036.1)]
其中, .corner() 方法并不是 “.corners”,因此不是返回一整个端点数组,而是根据给定的端点编号返回一个端点。
锚点中有两个点比较特殊,分别是 corner(0) 和 corner(7) ,这两个顶点分别代表坐标之和最小和最大的两个点,通过这两个点就可以还原整个范围。因此这两个顶点还可以专门用 .min 和 .max 方法来访问。
puts bb.min#>> Point3d(-17306.2, -30879.8, -8293.75)puts bb.max#>> Point3d(100884, 115512, 94036.1)
②长宽高与对角线
除了关键点以外,BoundingBox还提供四个与范围有关的长度参数,分别是“长”“宽”“高”(或者应该说是“宽”“高”“深”),和对角线长。其中, .width 对应的是x轴(红轴)方向上的宽度, .height 对应的是y轴(绿轴)方向上的宽度, .depth 对应的是z轴(蓝轴)方向上的宽度。 .diagonal 即对角线长度。
bb = Sketchup.active_model.boundsputs bb.width #>> ~ 3002041mmputs bb.height #>> ~ 3718342mmputs bb.depth #>> ~ 2599179mmputs bb.diagonal #>> ~ 5440041mm
当然也可以自己补充一个体积,在某些特定的场合可以使用:
module Geomclass BoundingBoxdef volumereturn self.height*self.width*self.depthendendend
(3)判断与运算
①判断是否在范围内
范围类的重要作用就是判断点是否在特定范围内,而这个功能需要 .contains? 方法来实现:
bb = Sketchup.active_model.boundsputs bb.contains?([0,0,0])puts bb.contains?(Geom::Point3d.new([2,54,-64]))
除了判断点位置, .contains? 方法也可以判断另一个范围类是否在此范围之内:
bb_model = Sketchup.active_model.boundsbb_ent = Sketchup.active_model.entities[0].boundsputs bb_model.contains?(bb_ent)#>> trueputs bb_model.contains?(Geom::BoundingBox.new)#>> false
只有前者完全包含后者(包括相切),才会返回 true。另外,如果作为参数的范围是空范围,包含的结果必然是 false。其原因如下:
bb=Geom::BoundingBox.newfor i in 0..2 doputs bb.min[i]>bb.max[i]end#>> true#>> true#>> true
可以发现一个新创建的空范围,它的max点要小于min点,这是检验范围是否有效的标志。而 .contains? 方法中需要对比两个范围的min点和max点,类似于如下的定义:
module Geomclass BoundingBoxdef contains?(bb_or_point)if bb_or_point.is_a?(::Array) then_max=bb_or_point_min=bb_or_pointelsif bb_or_point.is_a?(Geom::Point3d) then_max=bb_or_point.to_a_min=bb_or_point.to_aelsif bb_or_point.is_a?(Geom::BoundingBox) then_max=bb_or_point.max.to_a_min=bb_or_point.min.to_aelse return false end_min.each_index{|i|if _min[i]<self.min[i] then return false end}_max.each_index{|i|if _max[i]>self.max[i] then return false end}return trueendendend
因此,只有同时满足条件才会返回 true,所以空范围一定不能同时满足最大和最小两个要求。
②并集运算
BoundingBox 类实例也可以在原有范围的基础上追加坐标或范围,扩大包含给定的坐标或者范围,可以理解为范围的并集操作。这个功能需要 .add 方法来实现:
bb=Geom::BoundingBox.newbb.add([-100.mm,-100.mm,-300.mm])bb.add([0.mm,100.mm,100.mm])bb.add([200.mm,300.mm,100.mm])puts bb.minputs bb.max#>> (-100mm, -100mm, -300mm)#>> (200mm, 300mm, 100mm)
除了接受表示点坐标的Array类参数, .add 方法还可以接受 Geom:: Point3d 类、 Sketchup:: Vertex类和 Geom:: BoundingBox 类的实例:
bb.add(Geom::Point3d.new(-100.mm,-100.mm,-300.mm))#令当前模型至少包含一个边线图元ent=Sketchup.active_model.entities.grep(Sketchup::Edge)[0]bb.add(ent.vertices[0])bb.add(ent.bounds)
还可以接受以上这些类型实例组成的数组:
points_or_bb = []points_or_bb << Geom::Point3d.new(-100.mm,-100.mm,-300.mm)points_or_bb << ent.vertices[0]points_or_bb << ent.boundsbb.add(points_or_bb)
③交集运算
BoundingBox 类实例同样也可以进行交集运算,这个功能需要 .intersect 方法来实现:
#令当前模型包含两个群组ents=Sketchup.active_model.entities.grep(Sketchup::Group)bb=ents[0].bounds.intersect(ents[1].bounds)puts bb.widthputs bb.heightputs bb.depth#>> ~ 1374mm#>> ~ 1089mm#>> ~ 2110mm
以上代码计算两个群组的范围交叠部分,示意图如下(其中立方体为辅助显示范围大小):
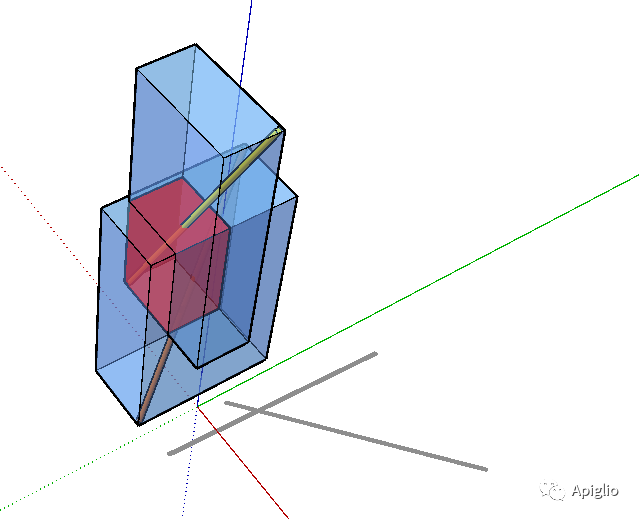
交集运算和并集运算的原理都是判断min点和max点的坐标是否需要更新,有兴趣的可以自己仿写练习。
最后还是按照惯例放一些补充内容。本部分最后一张图的立方体不是手工创建的,而是通过以下代码生成的:
module Geomclass BoundingBoxdef create_boxp=[]for point_id in 0..3 dop << self.corner(point_id)endents=Sketchup.active_model.entitiesgrp=ents.add_grouplines=[]lines << (grp.entities.add_line(p[0],p[1]))lines << (grp.entities.add_line(p[1],p[3]))lines << (grp.entities.add_line(p[3],p[2]))lines << (grp.entities.add_line(p[2],p[0]))f=grp.entities.add_face linesf.pushpull self.depthreturn grpendendend
其中包括一些有关图元类的代码,在后续的教程中会继续介绍。有关图元的代码有很多例子已经出现在往期的其他文章中,例如:
本文编号:SU-R07
