这篇里介绍的核-PCA 算法在不直接提供映射函数的情况下试图实现在高维空间中线性可分。这似乎有点儿 又要马儿跑得快，又要马儿不吃草 的意思。

本篇来看另一个经典算法，随机 SVD 分解。如果要用一句话来概括的话，我选 投机取巧，以小博大: 指用小的成本通过冒险投机手段换取大的价值。如果将这里的投机两字改成随机，那也许就再合适不过了。

1引言

调用 sklearn 里的 PCA，你可能会发现有个参数 svd_solver 可以设置 svd_solver = 'randomized'。这里的随机是什么意思呢？如果用默认设置 'auto' 的话，那么会根据矩阵大小自动选择求解器。它会基于 X.shape 和 n_components 的值默认选择求解器：如果输入数据大于 500x500，并且要提取的组件数小于数据最小维度的 80％，则使用效率更高的随机化 SVD 方法。否则，将计算出精确的完整版 SVD。

那么，所谓的随机 SVD 分解是怎么回事呢？本文就是为了揭开这个，让大家快速 get 到很多时候 SVD 分解是这么来求解的。

矩阵分解是解决许多机器学习问题的有力工具，已被广泛用于数据压缩、降维和稀疏学习等。在矩阵低秩逼近的应用需求方面，奇异值分解（SVD）通常被证明是最佳选择。但是，对于比较大的矩阵（例如）的精确 SVD 分解在计算上具有挑战性。为了应对这种实战情况，提出了很多基于随机线性代数的算法，其中最重要的算法之一是随机 SVD，在分解具有较低秩的大型矩阵时表现出色。

SVD 技术发展时间表

本篇将介绍随机 SVD 的初步思想，是目前实际版本的基础。为了帮助读者更好地理解随机 SVD，我们在本文中还提供了相应的 Python 实现。

2SVD 分解

首先回顾一下 SVD 的概念。我们知道，SVD 是线性代数中最重要的分解公式之一。对于任何给定的矩阵，SVD 分解的形式为，

\mathbf{A} = \mathbf{U\Sigma V}^{\top}

其中矩阵和分别由左和右奇异向量组成，的对角元素是奇异值。

.小矩阵示例

以一个矩阵为例，我们可以在 Python 中使用 numpy.linalg.svd() 计算 SVD，

\mathbf{A}=\left(\begin{array}{cccc} 1 & 3 & 2 \\ 5 & 3 & 1 \\ 3 & 4 & 5 \\ \end{array}\right)\in\mathbb{R}^{3\times 3}.

import numpy as np

A = np.array([[1, 3, 2],
              [5, 3, 1],
              [3, 4, 5]])

u, s, v = np.linalg.svd(A, full_matrices = 0)

print('Left singular vectors:')
print(u)
print()
print('Singular values:')
print(s)
print()
print('Right singular vectors:')
print(v)
print()

Left singular vectors:
[[-0.37421754  0.28475648 -0.88253894]
 [-0.56470638 -0.82485997 -0.02669705]
 [-0.7355732   0.48838486  0.46948087]]

Singular values:
[9.34265841 3.24497827 1.08850813]

Right singular vectors:
[[-0.57847229 -0.61642675 -0.53421706]
 [-0.73171177  0.10269066  0.67383419]
 [ 0.36051032 -0.78068732  0.51045041]]

在这个例子中，奇异值为 9.3427、3.2450 和 1.0885。

3随机 SVD

.基本思想

0：确定目标秩。
1：使用随机投影采样列空间，找到一个列矩阵，其列近似表示的列空间，即。
2：将投影到子空间，即，并在上计算 SVD 分解。
3：使用以及的 SVD 分解得到的左奇异向量。

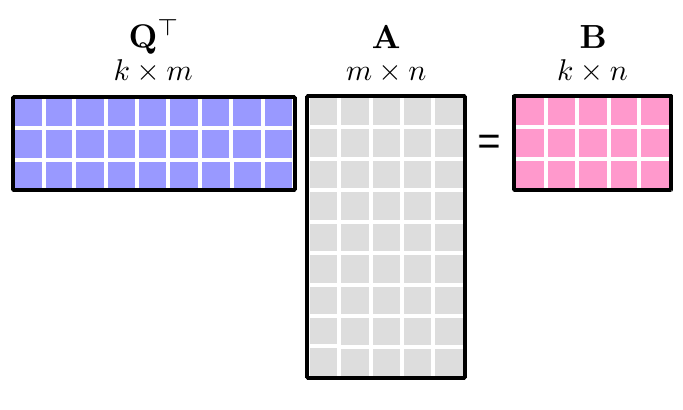
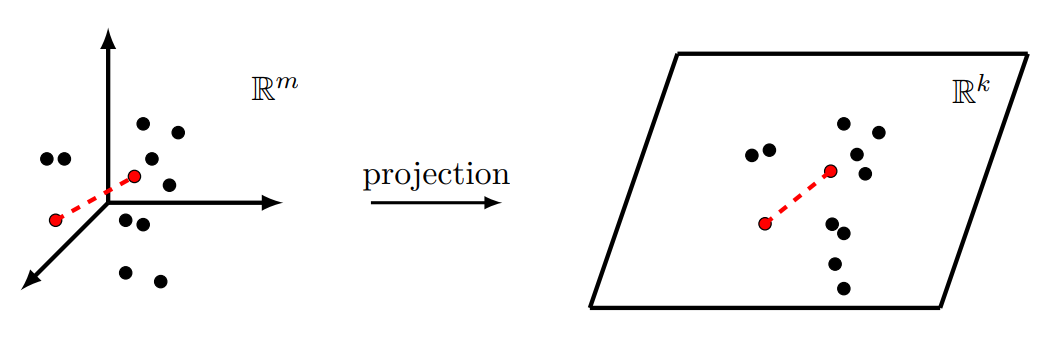
所谓的以小博大是指将大矩阵通过一组正交基（至于怎么来，下文再介绍）转化成一个小矩阵。然后，通过分解小矩阵来得到大矩阵的分解。这个大小矩阵的转化过程请参考下面两个图。

上面步骤可以浓缩为下面几个公式，

\mathbf{B}=\mathbf{Q}^{\top} \mathbf{A} = \mathbf{U_{B}\Sigma_{B} V_{B}}^{\top}

\mathbf{A} \approx \mathbf{Q}\mathbf{Q}^{\top} \mathbf{A} = \mathbf{Q}\mathbf{B}=\mathbf{Q}\mathbf{U_{B}\Sigma_{B} V_{B}}^{\top}

\mathbf{A} \approx \mathbf{Q}\mathbf{U_{B}\Sigma_{B} V_{B}}^{\top} = \mathbf{U\Sigma_{B} V_{B}}^{\top}

最后得到的分解，并且左奇异向量为，

\mathbf{U} = \mathbf{Q U_{B}}

.详细步骤

对照随机 SVD 上面的 1、2、3 三个步骤。对于任何给定的矩阵，如果给秩加上约束条件，则第 1 步具体展开是，

a）生成大小为的高斯随机矩阵，
b）计算一个新的矩阵，
c）将 QR 分解应用于矩阵。

随机投影矩阵可以用于对输入矩阵的列空间进行采样，最终目的是构建一个正交投影矩阵。

通过从标准正态分布中首先采样一组个随机向量来构造随机投影矩阵。概率论可以确保随机向量以高概率线性无关。然后，将的列通过投影矩阵映射到低维空间来得到矩阵。

换句话说，此过程形成一组线性无关的关于列的随机加权线性组合，并将列数从减少到。

有了矩阵，只需通过 QR 分解就可以得到的一组标准正交基。有了，我们就可以将转化为小矩阵了，这点在前面交代过了。

随机 SVD 分解的第 1 步

可以感觉到，整个算法比较核心的环节就是构建矩阵 。可以说它就是大矩阵的浓缩版本，只是列要少得多。

请注意，第 1 步需要返回矩阵。紧接着，我们来看第 2 、3 步，

a）通过将和矩阵相乘得出矩阵，即，
b）计算矩阵的 SVD，用于代替计算原始矩阵的 SVD。这里，是一个较小的矩阵。

请注意，矩阵的奇异值（即）和右奇异向量（即）也是矩阵的奇异值和右奇异向量。

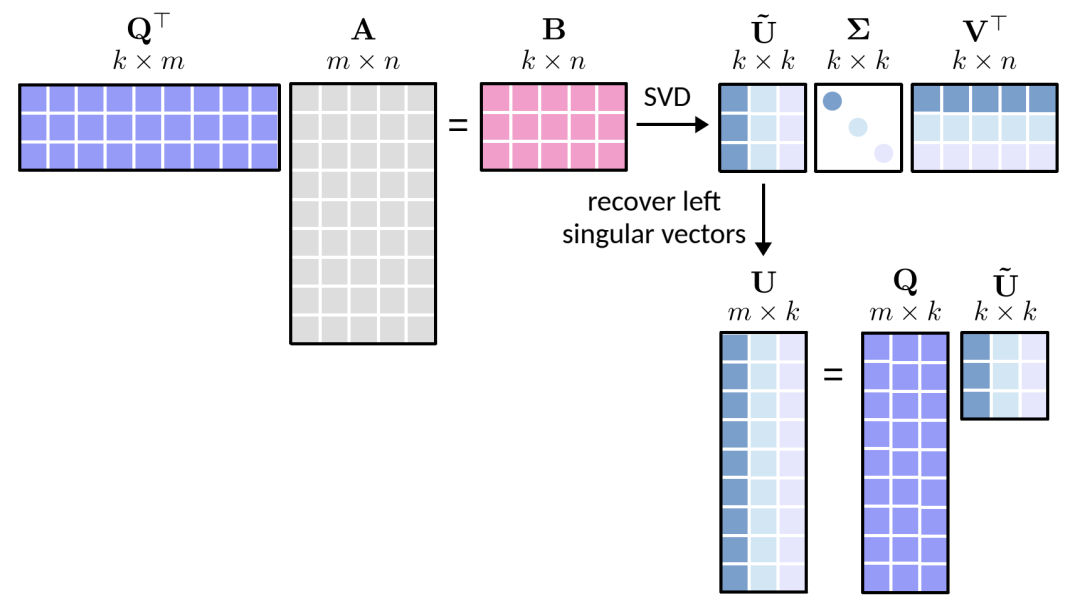
随机 SVD 分解的后面两步

.小矩阵示例

即使我们已经在上面学习了随机化 SVD 的基本思想，但是如果没有直观的例子，可能还不是很清楚。为此，我们遵循前面提到的小矩阵 SVD。

首先，让我们尝试为随机 SVD 编写 Python 函数。在这里，我们将使用两个 Numpy 函数，即 np.linalg.qr() 和 np.linalg.svd()。

import numpy as np

def rsvd(A, Omega):
    Y = A @ Omega
    Q, _ = np.linalg.qr(Y)
    B = Q.T @ A
    u_tilde, s, v = np.linalg.svd(B, full_matrices = 0)
    u = Q @ u_tilde
    return u, s, v

现在，让我们使用 3×3 矩阵对其进行测试，rank = 2 用于指定。

np.random.seed(1000)
A = np.array([[1, 3, 2],
              [5, 3, 1],
              [3, 4, 5]])
rank = 2
Omega = np.random.randn(A.shape[1], rank)
u, s, v = rsvd(A, Omega)
print('Left singular vectors:')
print(u)
print()
print('Singular values:')
print(s)
print()
print('Right singular vectors:')
print(v)
print()

Left singular vectors:
[[ 0.38070859  0.60505354]
 [ 0.56830191 -0.74963644]
 [ 0.72944767  0.26824507]]

Singular values:
[9.34224023 3.02039888]

Right singular vectors:
[[ 0.57915029  0.61707064  0.53273704]
 [-0.77420021  0.21163814  0.59650929]]

回想一下，此矩阵的奇异值为 9.3427，3.2450 和 1.0885。在这种情况下，随机 SVD 的前两个奇异值为 9.3422 和 3.0204。

我们可以看到，这两个 SVD 算法计算出的第一个奇异值非常接近。但是，随机 SVD 的第二个奇异值稍微有点偏差。那么，自然要问了，有什么方法可以改善这个结果吗？如何改呢？答案是肯定的，请看下一节。

4幂次迭代法随机 SVD

为了提高随机 SVD 的精度，可以在上面第 1 步中直接使用幂次迭代方法。

在以下 Python 代码中，power_iteration() 是用于迭代计算矩阵的函数（默认的 power_iter为 3），然后通过 QR 分解方式得到 - 矩阵。

import numpy as np

def power_iteration(A, Omega, power_iter = 3):
    Y = A @ Omega
    for q in range(power_iter):
        Y = A @ (A.T @ Y)
    Q, _ = np.linalg.qr(Y)
    return Q

def rsvd(A, Omega):
    Q = power_iteration(A, Omega)
    B = Q.T @ A
    u_tilde, s, v = np.linalg.svd(B, full_matrices = 0)
    u = Q @ u_tilde
    return u, s, v

让我们测试新的 rsvd() 函数。

np.random.seed(1000)

A = np.array([[1, 3, 2],
              [5, 3, 1],
              [3, 4, 5]])
rank = 2
Omega = np.random.randn(A.shape[1], rank)
u, s, v = rsvd(A, Omega)
print('Left singular vectors:')
print(u)
print()
print('Singular values:')
print(s)
print()
print('Right singular vectors:')
print(v)
print()

Left singular vectors:
[[ 0.37421757  0.28528579]
 [ 0.56470638 -0.82484381]
 [ 0.73557319  0.48810317]]

Singular values:
[9.34265841 3.24497775]

Right singular vectors:
[[ 0.57847229  0.61642675  0.53421706]
 [-0.73178429  0.10284774  0.67373147]]

参考资料

[1]

Randomized Matrix Decompositions Using R.: https://arxiv.org/pdf/1608.02148.pdf

[2]

Randomized Singular Value Decomposition: http://gregorygundersen.com/blog/2019/01/17/randomized-svd/

[3]

Xinyu Chen: https://radiant-brushlands-42789.herokuapp.com/towardsdatascience.com/intuitive-understanding-of-randomized-singular-value-decomposition-9389e27cb9de

相关阅读