马斯克常挂嘴边的「第一性原理」，还是DeepMind对付薛定谔猫的重要工具

昨日，DeepMind发布了利用第一性原理指导深度学习进行量子力学研究的代码，以便更好地计算物理学和化学并将其应用到更广泛的问题上。

该团队开发了一种新的神经网络结构「Fermionic Neural Network」，简称 FermiNet ，它非常适合于模拟大量电子的量子态，而这些电子正是化学键的基本组成部分。

FermiNet 首次展示了从第一性原理来将深度学习技术应用于计算原子和分子的能量，并且达到了可以使用的精度，是迄今为止最精确的神经网络方法。

FermiNet 未来还将承担在蛋白质折叠、玻璃动力学、晶格量子色动力学和许多其他项目上的工作，将这一愿景变为现实。

量子力学简史：不可不说的「薛定谔的猫」

提到「量子力学」 这个词，就会让人想起「薛定谔的猫」，既可以是活的也可以是死的，还有一些基本粒子，既是粒子也是波。

在量子系统中，像电子这样的粒子并不像经典物理描述中的粒子那样有确切的位置。相反，它的位置被概率所描述：它会以不同的概率分散在各个地方。

这种违反直觉的状态导致物理学家费曼曾经宣称: 「如果你认为你理解量子力学，你就不理解量子力学」。

尽管这种现象十分怪异，但是这个理论的核心可以简化为几个简单的方程式，其中最著名的是薛定谔方程，它描述了量子尺度下粒子的行为，就像牛顿定律描述了经典物理尺度下物体的行为一样。

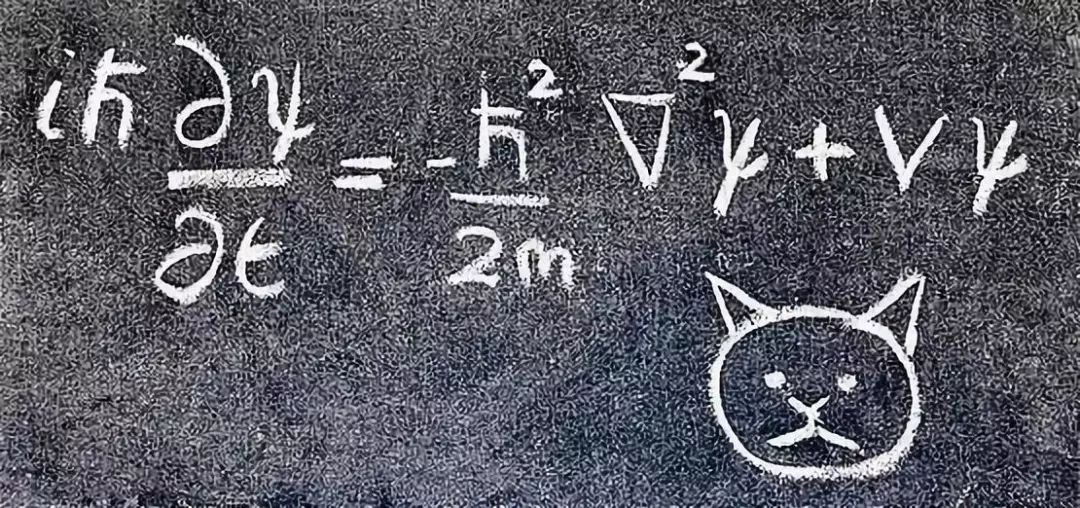
这些方程式足以描述我们在原子和原子核水平上看到的所有熟悉物质的行为。它们违反直觉的本性导致了各种奇特的现象: 超导体、超流体、激光等。

物理学家保罗 · 狄拉克说，「我们已经完全了解大部分物理学和整个化学的数学理论所必需的基本物理定律，而困难的只是这些定律的准确应用方程过于复杂而难以求解。因此，我们有必要开发一些近似的应用量子力学的实用方法」。

FermiNet：费米神经网络

尽管现有的计算量子力学工具有很多，但是还需要一个新的方法来解决高效表示的问题。这就是为什么即使是最近似的方法，最大的量子化学计算也只能求解数以万计的电子，而经典的化学计算技术如分子动力学则能处理数以百万计的原子。

经典系统的状态可以用很简单的方法表示：只需要跟踪每个粒子的位置和动量即可。而描述量子系统的状态要困难得多。必须给每一种可能的电子位置构型创建对应的概率分布。

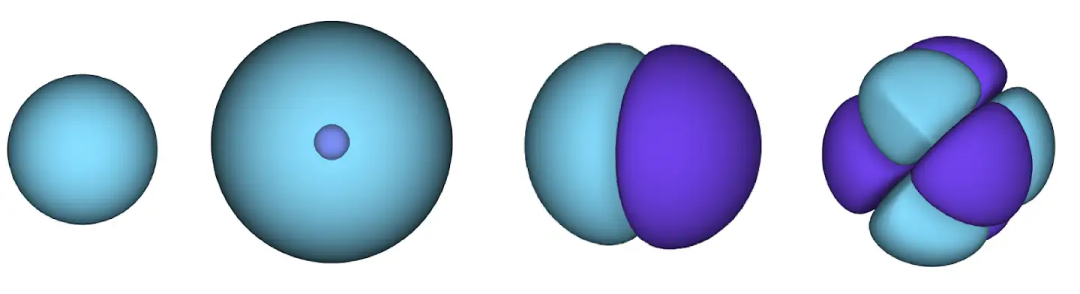
这些会被编码在波函数中，波函数给每个电子组态赋予一个正数或负数，波函数的平方给出了在这个组态中找到系统的概率。

而要描述电子组态所有可能的位置，几乎是不可能的，因为假设每个维度上有100个网格，则可能的电子配置的数量将大于宇宙中的所有原子数量！

而这正是DeepMind团队认为深层神经网络可以起到帮助的地方。

在过去的几年中，神经网络在表示复杂的、高维的概率分布方面取得了巨大的进展，现在也可以高效且可伸缩地训练这些网络。

DeepMind成员认为，既然这些网络已经证明了它们在人工智能问题中拟合高维函数的能力，也许它们也可以用来表示量子波函数。

在处理电子时只有一个问题就是：电子必须服从「泡利不相容原理」，这意味着它们不可能同时处于同一空间。

这是因为电子是一种被称为「费米子」的粒子，包括大多数物质的组成部分如质子、中子、夸克、中微子等都是费米子粒子。

它们的波函数一定是反对称的，如果你交换两个电子的位置，波函数就会乘以 -1。这意味着，如果两个电子相互叠加，波函数(以及这种构型的概率)将为零。

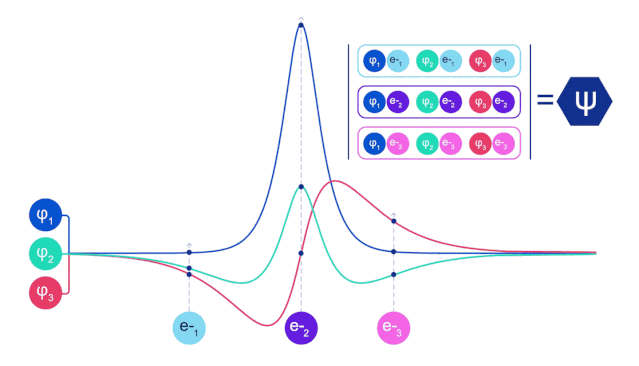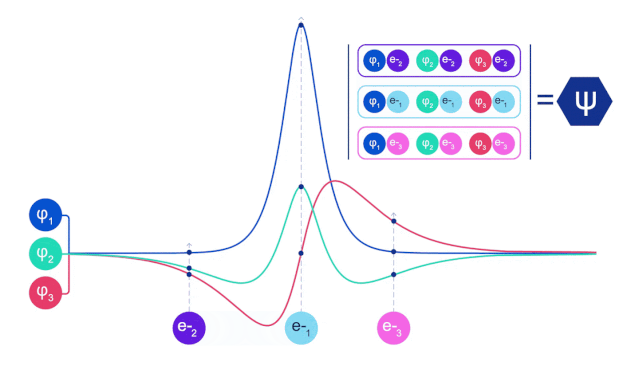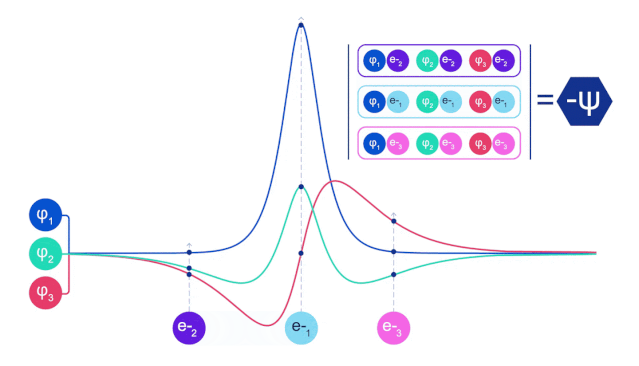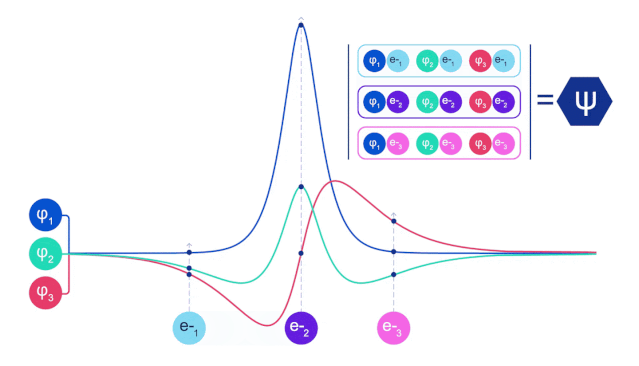
这意味着必须开发一种新型的神经网络，它的输入是反对称的，也就是「费米子神经网络」，或者 「FermiNet」。

在大多数量子化学方法中，反对称性是用一个行列式的函数引入的。矩阵的行列式具有这样的性质，如果你交换两行，输出就会乘以 -1，就像费米子的波函数一样。

所以你可以取一堆单电子函数，对系统中的每个电子进行求值，然后把所有的结果存到一个矩阵中，这个矩阵的行列式就是一个恰当的反对称波函数。

在表示复杂函数时，深层神经网络往往比基函数的线性组合有效得多。

在 FermiNet 中，这是通过使进入行列式的每个函数成为所有电子的函数来实现的。这远远超出了只使用单电子和双电子函数的方法。

FermiNet 对每个电子都有一个独立的信息流。如果这些数据流之间没有任何交互，这个网络就不会比传统的斯莱特行列式网络更具表现力。

与斯莱特行列式不同，FermiNets 是通用函数逼近器，这就意味着，如果我们能够正确地训练这些网络，它们应该能够适应薛定谔方程的近乎精确的解。

我们通过最小化系统能量来拟合FermiNet。为了精确地做到这一点，需要在所有可能的电子构型下计算波函数，所以需要近似计算。

随机选择电子构型，计算每个电子构型的局部能量，把每个构型的贡献加起来，最小化这个能量，而不是真正的能量，这被称为「蒙特卡罗方法」，因为它有点像一个赌徒一遍又一遍地掷骰子。虽然它是近似的，如果我们需要使它更准确，我们总是可以再掷骰子。

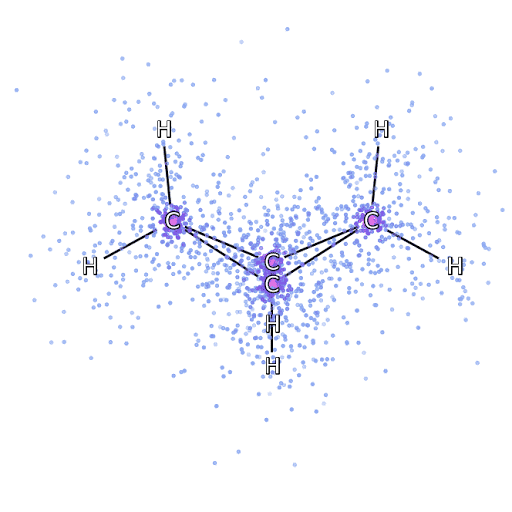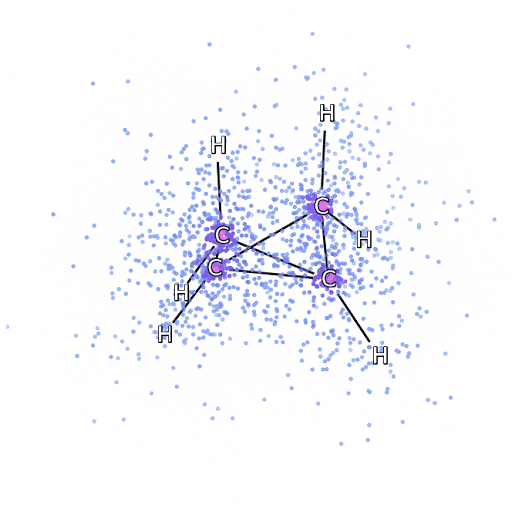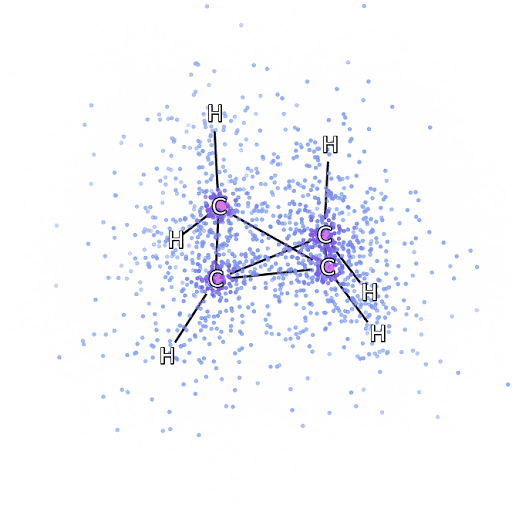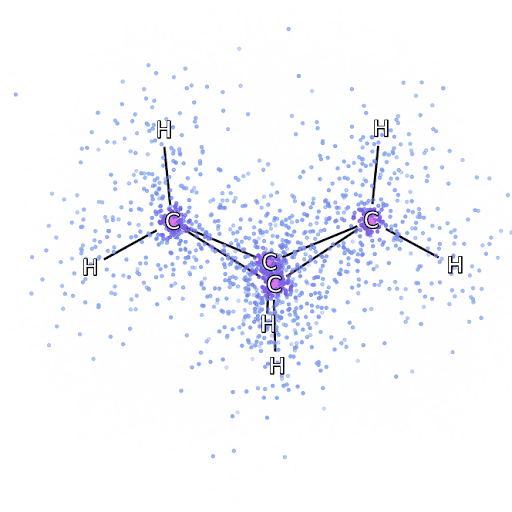
为了确保 FermiNet 确实代表了最先进技术，研究人员从研究简单透彻的系统开始，比如第一排元素周期表中的原子。这些都是很小的系统，如10个或更少的电子，而且结构非常简单，可以用最精确(但是指数缩放)的方法来处理。

FermiNet 的性能优于可比的 VMC 计算，而且提升很大，通常将相对于指数缩放计算的误差减少一半或更多。

把 FermiNet 应用到更大的分子上，从氢化锂开始，一直到双环丁烷，观察到的最大的系统，有30个电子。对于最小的分子，FermiNet 捕获了令人震惊的 99.8% 的耦合团簇能量和从单个斯莱特行列式所获得的能量之间的差异。对于丁烷，FermiNet 也捕获了这种相关能量的97% 或者更多，这和传统方法相比是一个巨大的提升。

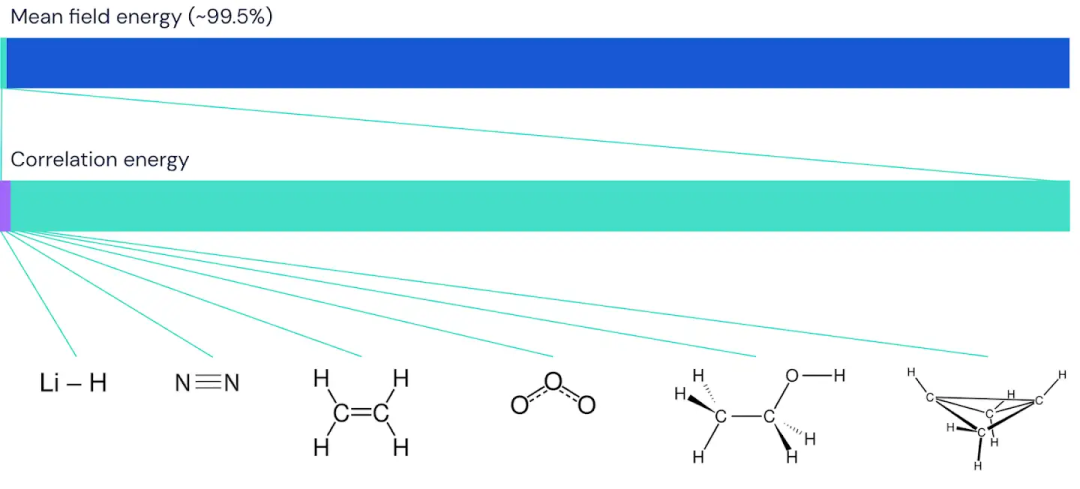
DeepMind 认为 FermiNet 是将深度学习和计算量子化学融合的开端。到目前为止，大多数系统都已经得到了很好的研究和理解。但是，正如深度学习在其他领域取得的第一个成果带来了大量的后续工作和快速进展一样，希望 FermiNet 也可以激发大量的工作，扩大规模，并为新的甚至更好的网络架构提出许多想法。

将深度学习应用于多电子问题的第一性原理计算，DeepMind也只是触及了量子物理学的皮毛，期待着将 FermiNet 应用到材料科学和凝聚态物理学的棘手问题上。最重要的是，DeepMind希望通过发布实验中使用的源代码，可以激励其他研究人员在他们工作的基础上，尝试一些从未想过的新想法。